Learning optimal objective values for MILP

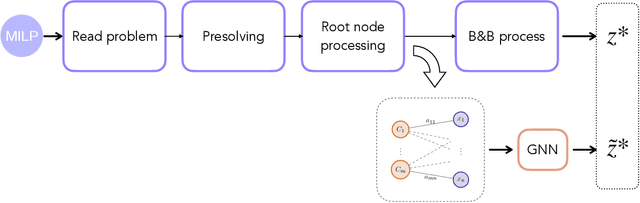
Modern Mixed Integer Linear Programming (MILP) solvers use the Branch-and-Bound algorithm together with a plethora of auxiliary components that speed up the search. In recent years, there has been an explosive development in the use of machine learning for enhancing and supporting these algorithmic components. Within this line, we propose a methodology for predicting the optimal objective value, or, equivalently, predicting if the current incumbent is optimal. For this task, we introduce a predictor based on a graph neural network (GNN) architecture, together with a set of dynamic features. Experimental results on diverse benchmarks demonstrate the efficacy of our approach, achieving high accuracy in the prediction task and outperforming existing methods. These findings suggest new opportunities for integrating ML-driven predictions into MILP solvers, enabling smarter decision-making and improved performance.

Machine Learning Augmented Branch and Bound for Mixed Integer Linear Programming

Mixed Integer Linear Programming (MILP) is a pillar of mathematical optimization that offers a powerful modeling language for a wide range of applications. During the past decades, enormous algorithmic progress has been made in solving MILPs, and many commercial and academic software packages exist. Nevertheless, the availability of data, both from problem instances and from solvers, and the desire to solve new problems and larger (real-life) instances, trigger the need for continuing algorithmic development. MILP solvers use branch and bound as their main component. In recent years, there has been an explosive development in the use of machine learning algorithms for enhancing all main tasks involved in the branch-and-bound algorithm, such as primal heuristics, branching, cutting planes, node selection and solver configuration decisions. This paper presents a survey of such approaches, addressing the vision of integration of machine learning and mathematical optimization as complementary technologies, and how this integration can benefit MILP solving. In particular, we give detailed attention to machine learning algorithms that automatically optimize some metric of branch-and-bound efficiency. We also address how to represent MILPs in the context of applying learning algorithms, MILP benchmarks and software.

Learning to branch with Tree MDPs

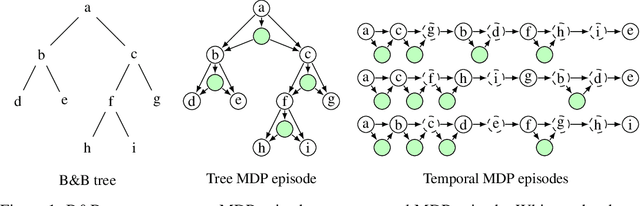
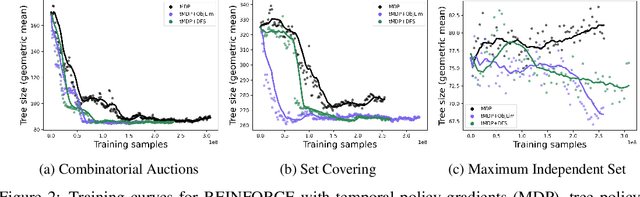
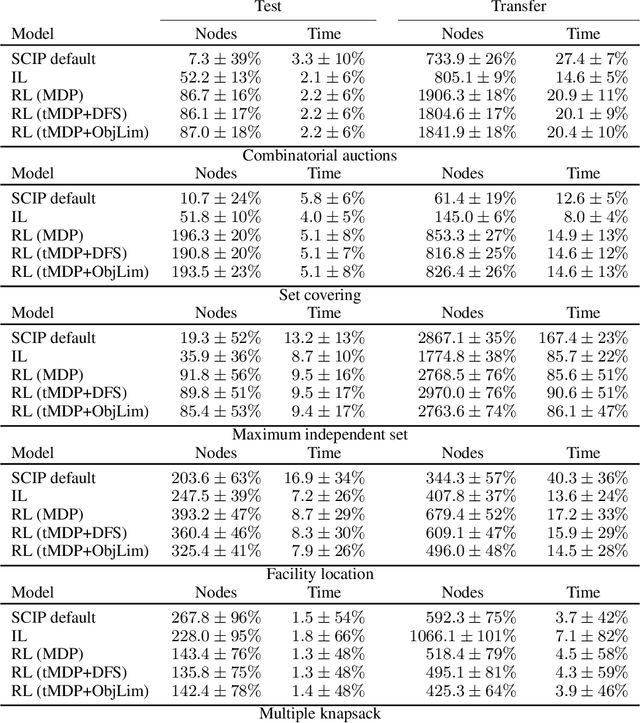
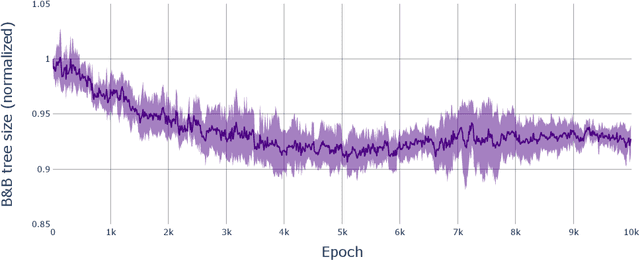
State-of-the-art Mixed Integer Linear Program (MILP) solvers combine systematic tree search with a plethora of hard-coded heuristics, such as the branching rule. The idea of learning branching rules from data has received increasing attention recently, and promising results have been obtained by learning fast approximations of the strong branching expert. In this work, we instead propose to learn branching rules from scratch via Reinforcement Learning (RL). We revisit the work of Etheve et al. (2020) and propose tree Markov Decision Processes, or tree MDPs, a generalization of temporal MDPs that provides a more suitable framework for learning to branch. We derive a tree policy gradient theorem, which exhibits a better credit assignment compared to its temporal counterpart. We demonstrate through computational experiments that tree MDPs improve the learning convergence, and offer a promising framework for tackling the learning-to-branch problem in MILPs.

The Machine Learning for Combinatorial Optimization Competition (ML4CO): Results and Insights

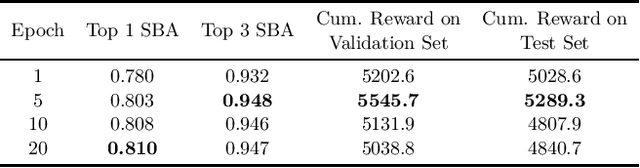
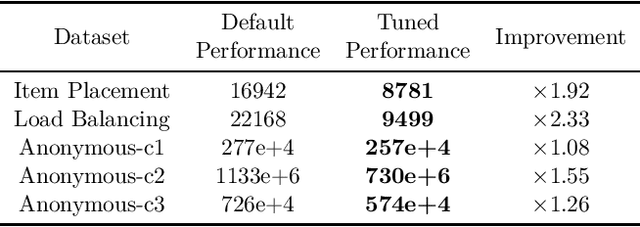
Combinatorial optimization is a well-established area in operations research and computer science. Until recently, its methods have focused on solving problem instances in isolation, ignoring that they often stem from related data distributions in practice. However, recent years have seen a surge of interest in using machine learning as a new approach for solving combinatorial problems, either directly as solvers or by enhancing exact solvers. Based on this context, the ML4CO aims at improving state-of-the-art combinatorial optimization solvers by replacing key heuristic components. The competition featured three challenging tasks: finding the best feasible solution, producing the tightest optimality certificate, and giving an appropriate solver configuration. Three realistic datasets were considered: balanced item placement, workload apportionment, and maritime inventory routing. This last dataset was kept anonymous for the contestants.

Ecole: A Gym-like Library for Machine Learning in Combinatorial Optimization Solvers

We present Ecole, a new library to simplify machine learning research for combinatorial optimization. Ecole exposes several key decision tasks arising in general-purpose combinatorial optimization solvers as control problems over Markov decision processes. Its interface mimics the popular OpenAI Gym library and is both extensible and intuitive to use. We aim at making this library a standardized platform that will lower the bar of entry and accelerate innovation in the field. Documentation and code can be found at https://www.ecole.ai.