Learning optimal objective values for MILP
Paper and Code
Nov 27, 2024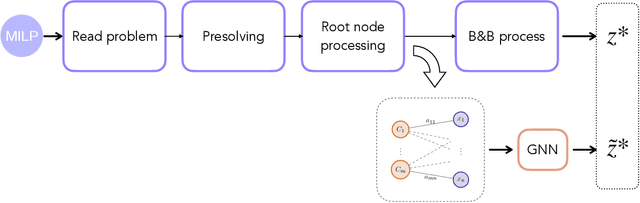


Modern Mixed Integer Linear Programming (MILP) solvers use the Branch-and-Bound algorithm together with a plethora of auxiliary components that speed up the search. In recent years, there has been an explosive development in the use of machine learning for enhancing and supporting these algorithmic components. Within this line, we propose a methodology for predicting the optimal objective value, or, equivalently, predicting if the current incumbent is optimal. For this task, we introduce a predictor based on a graph neural network (GNN) architecture, together with a set of dynamic features. Experimental results on diverse benchmarks demonstrate the efficacy of our approach, achieving high accuracy in the prediction task and outperforming existing methods. These findings suggest new opportunities for integrating ML-driven predictions into MILP solvers, enabling smarter decision-making and improved performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge