Change Point Detection by Cross-Entropy Maximization
Paper and Code
Sep 02, 2020
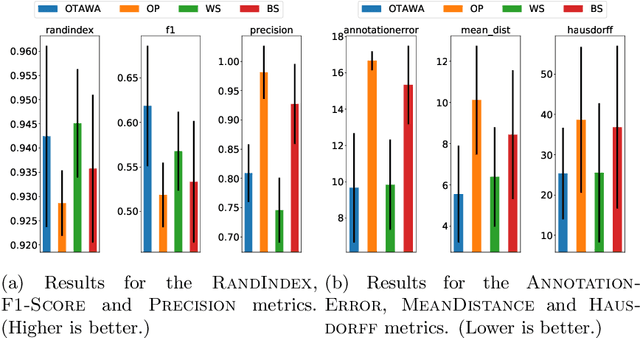
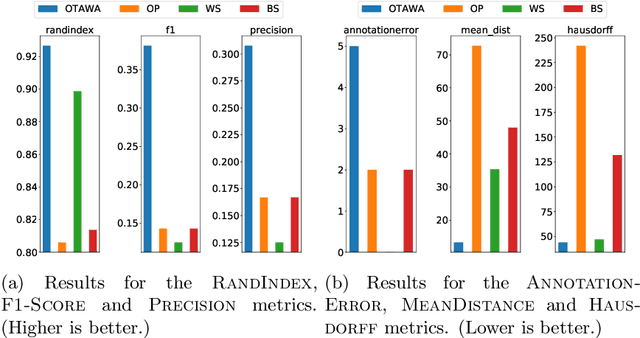
Many offline unsupervised change point detection algorithms rely on minimizing a penalized sum of segment-wise costs. We extend this framework by proposing to minimize a sum of discrepancies between segments. In particular, we propose to select the change points so as to maximize the cross-entropy between successive segments, balanced by a penalty for introducing new change points. We propose a dynamic programming algorithm to solve this problem and analyze its complexity. Experiments on two challenging datasets demonstrate the advantages of our method compared to three state-of-the-art approaches.
* Preprint
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge