GraIP: A Benchmarking Framework For Neural Graph Inverse Problems

A wide range of graph learning tasks, such as structure discovery, temporal graph analysis, and combinatorial optimization, focus on inferring graph structures from data, rather than making predictions on given graphs. However, the respective methods to solve such problems are often developed in an isolated, task-specific manner and thus lack a unifying theoretical foundation. Here, we provide a stepping stone towards the formation of such a foundation and further development by introducing the Neural Graph Inverse Problem (GraIP) conceptual framework, which formalizes and reframes a broad class of graph learning tasks as inverse problems. Unlike discriminative approaches that directly predict target variables from given graph inputs, the GraIP paradigm addresses inverse problems, i.e., it relies on observational data and aims to recover the underlying graph structure by reversing the forward process, such as message passing or network dynamics, that produced the observed outputs. We demonstrate the versatility of GraIP across various graph learning tasks, including rewiring, causal discovery, and neural relational inference. We also propose benchmark datasets and metrics for each GraIP domain considered, and characterize and empirically evaluate existing baseline methods used to solve them. Overall, our unifying perspective bridges seemingly disparate applications and provides a principled approach to structural learning in constrained and combinatorial settings while encouraging cross-pollination of existing methods across graph inverse problems.

Towards graph neural networks for provably solving convex optimization problems

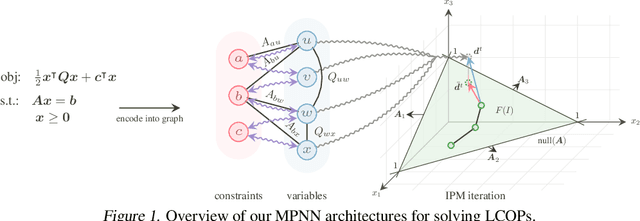
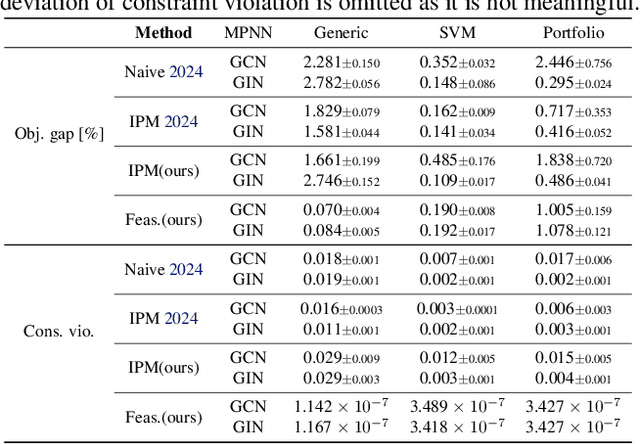
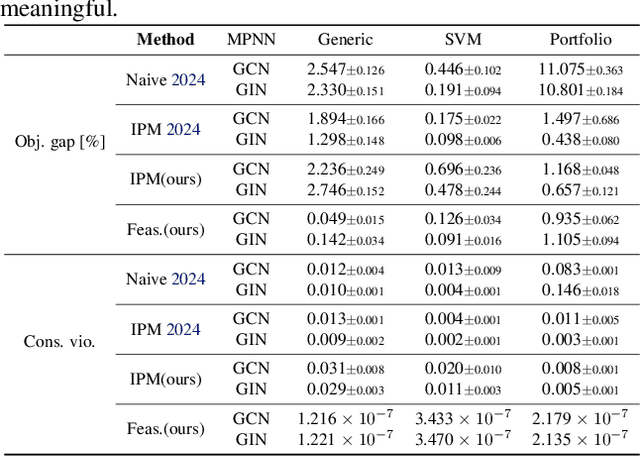
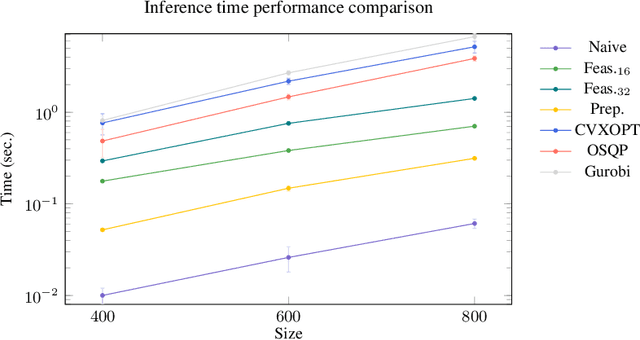
Recently, message-passing graph neural networks (MPNNs) have shown potential for solving combinatorial and continuous optimization problems due to their ability to capture variable-constraint interactions. While existing approaches leverage MPNNs to approximate solutions or warm-start traditional solvers, they often lack guarantees for feasibility, particularly in convex optimization settings. Here, we propose an iterative MPNN framework to solve convex optimization problems with provable feasibility guarantees. First, we demonstrate that MPNNs can provably simulate standard interior-point methods for solving quadratic problems with linear constraints, covering relevant problems such as SVMs. Secondly, to ensure feasibility, we introduce a variant that starts from a feasible point and iteratively restricts the search within the feasible region. Experimental results show that our approach outperforms existing neural baselines in solution quality and feasibility, generalizes well to unseen problem sizes, and, in some cases, achieves faster solution times than state-of-the-art solvers such as Gurobi.

Probabilistic Graph Rewiring via Virtual Nodes

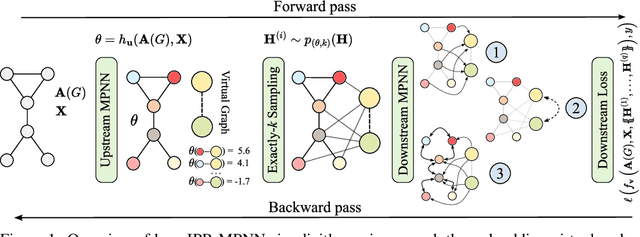
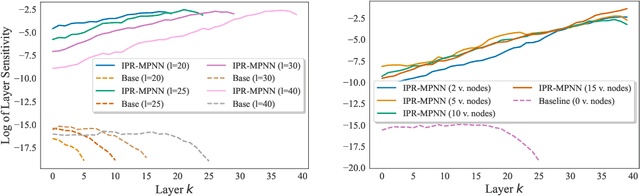
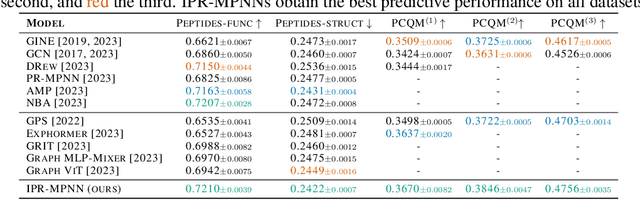
Message-passing graph neural networks (MPNNs) have emerged as a powerful paradigm for graph-based machine learning. Despite their effectiveness, MPNNs face challenges such as under-reaching and over-squashing, where limited receptive fields and structural bottlenecks hinder information flow in the graph. While graph transformers hold promise in addressing these issues, their scalability is limited due to quadratic complexity regarding the number of nodes, rendering them impractical for larger graphs. Here, we propose \emph{implicitly rewired message-passing neural networks} (IPR-MPNNs), a novel approach that integrates \emph{implicit} probabilistic graph rewiring into MPNNs. By introducing a small number of virtual nodes, i.e., adding additional nodes to a given graph and connecting them to existing nodes, in a differentiable, end-to-end manner, IPR-MPNNs enable long-distance message propagation, circumventing quadratic complexity. Theoretically, we demonstrate that IPR-MPNNs surpass the expressiveness of traditional MPNNs. Empirically, we validate our approach by showcasing its ability to mitigate under-reaching and over-squashing effects, achieving state-of-the-art performance across multiple graph datasets. Notably, IPR-MPNNs outperform graph transformers while maintaining significantly faster computational efficiency.

Exploring the Power of Graph Neural Networks in Solving Linear Optimization Problems

Recently, machine learning, particularly message-passing graph neural networks (MPNNs), has gained traction in enhancing exact optimization algorithms. For example, MPNNs speed up solving mixed-integer optimization problems by imitating computational intensive heuristics like strong branching, which entails solving multiple linear optimization problems (LPs). Despite the empirical success, the reasons behind MPNNs' effectiveness in emulating linear optimization remain largely unclear. Here, we show that MPNNs can simulate standard interior-point methods for LPs, explaining their practical success. Furthermore, we highlight how MPNNs can serve as a lightweight proxy for solving LPs, adapting to a given problem instance distribution. Empirically, we show that MPNNs solve LP relaxations of standard combinatorial optimization problems close to optimality, often surpassing conventional solvers and competing approaches in solving time.

Probabilistically Rewired Message-Passing Neural Networks

Message-passing graph neural networks (MPNNs) emerged as powerful tools for processing graph-structured input. However, they operate on a fixed input graph structure, ignoring potential noise and missing information. Furthermore, their local aggregation mechanism can lead to problems such as over-squashing and limited expressive power in capturing relevant graph structures. Existing solutions to these challenges have primarily relied on heuristic methods, often disregarding the underlying data distribution. Hence, devising principled approaches for learning to infer graph structures relevant to the given prediction task remains an open challenge. In this work, leveraging recent progress in exact and differentiable $k$-subset sampling, we devise probabilistically rewired MPNNs (PR-MPNNs), which learn to add relevant edges while omitting less beneficial ones. For the first time, our theoretical analysis explores how PR-MPNNs enhance expressive power, and we identify precise conditions under which they outperform purely randomized approaches. Empirically, we demonstrate that our approach effectively mitigates issues like over-squashing and under-reaching. In addition, on established real-world datasets, our method exhibits competitive or superior predictive performance compared to traditional MPNN models and recent graph transformer architectures.

Advancing Federated Learning in 6G: A Trusted Architecture with Graph-based Analysis

Integrating native AI support into the network architecture is an essential objective of 6G. Federated Learning (FL) emerges as a potential paradigm, facilitating decentralized AI model training across a diverse range of devices under the coordination of a central server. However, several challenges hinder its wide application in the 6G context, such as malicious attacks and privacy snooping on local model updates, and centralization pitfalls. This work proposes a trusted architecture for supporting FL, which utilizes Distributed Ledger Technology (DLT) and Graph Neural Network (GNN), including three key features. First, a pre-processing layer employing homomorphic encryption is incorporated to securely aggregate local models, preserving the privacy of individual models. Second, given the distributed nature and graph structure between clients and nodes in the pre-processing layer, GNN is leveraged to identify abnormal local models, enhancing system security. Third, DLT is utilized to decentralize the system by selecting one of the candidates to perform the central server's functions. Additionally, DLT ensures reliable data management by recording data exchanges in an immutable and transparent ledger. The feasibility of the novel architecture is validated through simulations, demonstrating improved performance in anomalous model detection and global model accuracy compared to relevant baselines.

Influence-Based Mini-Batching for Graph Neural Networks

Using graph neural networks for large graphs is challenging since there is no clear way of constructing mini-batches. To solve this, previous methods have relied on sampling or graph clustering. While these approaches often lead to good training convergence, they introduce significant overhead due to expensive random data accesses and perform poorly during inference. In this work we instead focus on model behavior during inference. We theoretically model batch construction via maximizing the influence score of nodes on the outputs. This formulation leads to optimal approximation of the output when we do not have knowledge of the trained model. We call the resulting method influence-based mini-batching (IBMB). IBMB accelerates inference by up to 130x compared to previous methods that reach similar accuracy. Remarkably, with adaptive optimization and the right training schedule IBMB can also substantially accelerate training, thanks to precomputed batches and consecutive memory accesses. This results in up to 18x faster training per epoch and up to 17x faster convergence per runtime compared to previous methods.

Ordered Subgraph Aggregation Networks

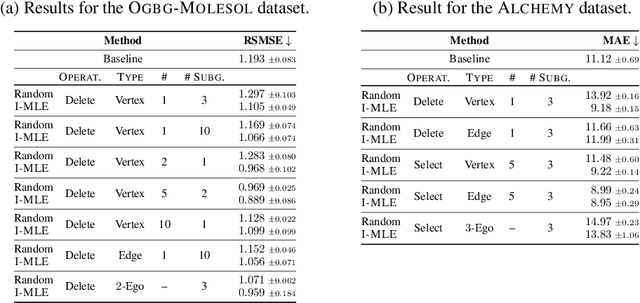
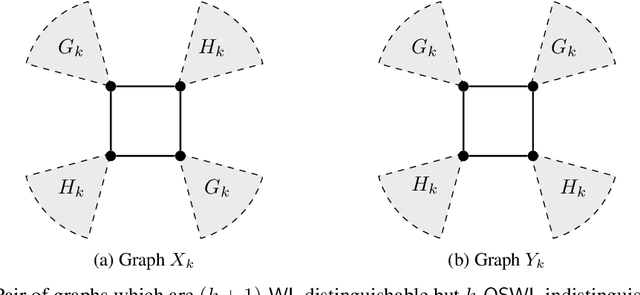
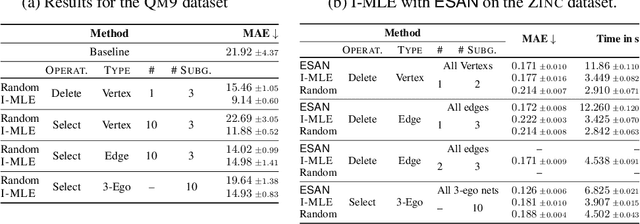
Numerous subgraph-enhanced graph neural networks (GNNs) have emerged recently, provably boosting the expressive power of standard (message-passing) GNNs. However, there is a limited understanding of how these approaches relate to each other and to the Weisfeiler--Leman hierarchy. Moreover, current approaches either use all subgraphs of a given size, sample them uniformly at random, or use hand-crafted heuristics instead of learning to select subgraphs in a data-driven manner. Here, we offer a unified way to study such architectures by introducing a theoretical framework and extending the known expressivity results of subgraph-enhanced GNNs. Concretely, we show that increasing subgraph size always increases the expressive power and develop a better understanding of their limitations by relating them to the established $k\text{-}\mathsf{WL}$ hierarchy. In addition, we explore different approaches for learning to sample subgraphs using recent methods for backpropagating through complex discrete probability distributions. Empirically, we study the predictive performance of different subgraph-enhanced GNNs, showing that our data-driven architectures increase prediction accuracy on standard benchmark datasets compared to non-data-driven subgraph-enhanced graph neural networks while reducing computation time.