Ordered Subgraph Aggregation Networks
Paper and Code
Jun 28, 2022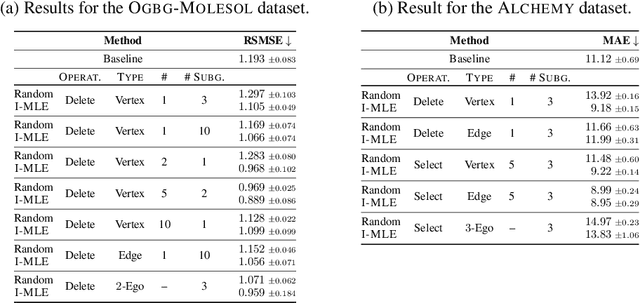
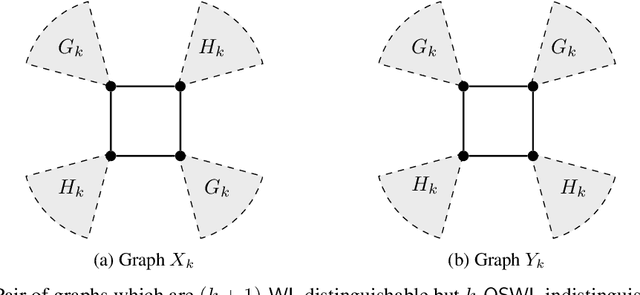
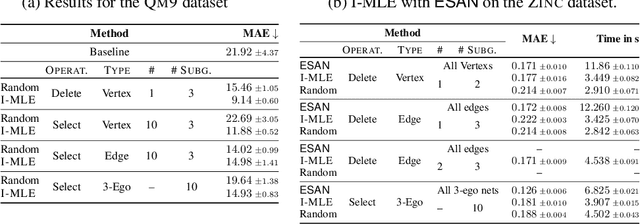

Numerous subgraph-enhanced graph neural networks (GNNs) have emerged recently, provably boosting the expressive power of standard (message-passing) GNNs. However, there is a limited understanding of how these approaches relate to each other and to the Weisfeiler--Leman hierarchy. Moreover, current approaches either use all subgraphs of a given size, sample them uniformly at random, or use hand-crafted heuristics instead of learning to select subgraphs in a data-driven manner. Here, we offer a unified way to study such architectures by introducing a theoretical framework and extending the known expressivity results of subgraph-enhanced GNNs. Concretely, we show that increasing subgraph size always increases the expressive power and develop a better understanding of their limitations by relating them to the established $k\text{-}\mathsf{WL}$ hierarchy. In addition, we explore different approaches for learning to sample subgraphs using recent methods for backpropagating through complex discrete probability distributions. Empirically, we study the predictive performance of different subgraph-enhanced GNNs, showing that our data-driven architectures increase prediction accuracy on standard benchmark datasets compared to non-data-driven subgraph-enhanced graph neural networks while reducing computation time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge