The Complexity of Symmetry Breaking Beyond Lex-Leader

Symmetry breaking is a widely popular approach to enhance solvers in constraint programming, such as those for SAT or MIP. Symmetry breaking predicates (SBPs) typically impose an order on variables and single out the lexicographic leader (lex-leader) in each orbit of assignments. Although it is NP-hard to find complete lex-leader SBPs, incomplete lex-leader SBPs are widely used in practice. In this paper, we investigate the complexity of computing complete SBPs, lex-leader or otherwise, for SAT. Our main result proves a natural barrier for efficiently computing SBPs: efficient certification of graph non-isomorphism. Our results explain the difficulty of obtaining short SBPs for important CP problems, such as matrix-models with row-column symmetries and graph generation problems. Our results hold even when SBPs are allowed to introduce additional variables. We show polynomial upper bounds for breaking certain symmetry groups, namely automorphism groups of trees and wreath products of groups with efficient SBPs.

Ordered Subgraph Aggregation Networks

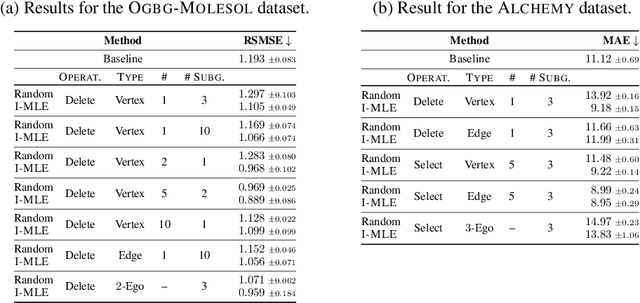
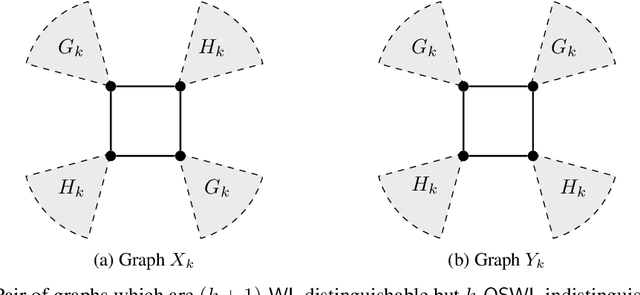
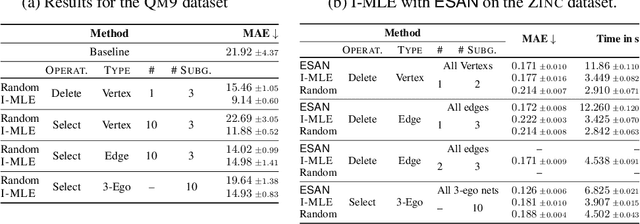
Numerous subgraph-enhanced graph neural networks (GNNs) have emerged recently, provably boosting the expressive power of standard (message-passing) GNNs. However, there is a limited understanding of how these approaches relate to each other and to the Weisfeiler--Leman hierarchy. Moreover, current approaches either use all subgraphs of a given size, sample them uniformly at random, or use hand-crafted heuristics instead of learning to select subgraphs in a data-driven manner. Here, we offer a unified way to study such architectures by introducing a theoretical framework and extending the known expressivity results of subgraph-enhanced GNNs. Concretely, we show that increasing subgraph size always increases the expressive power and develop a better understanding of their limitations by relating them to the established $k\text{-}\mathsf{WL}$ hierarchy. In addition, we explore different approaches for learning to sample subgraphs using recent methods for backpropagating through complex discrete probability distributions. Empirically, we study the predictive performance of different subgraph-enhanced GNNs, showing that our data-driven architectures increase prediction accuracy on standard benchmark datasets compared to non-data-driven subgraph-enhanced graph neural networks while reducing computation time.

SpeqNets: Sparsity-aware Permutation-equivariant Graph Networks

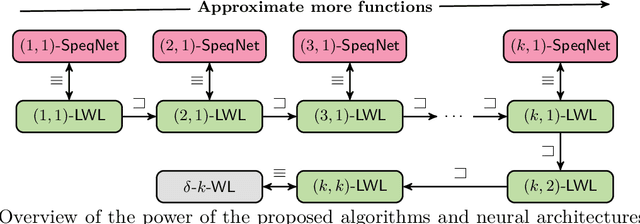
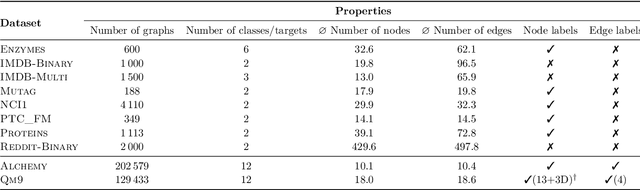
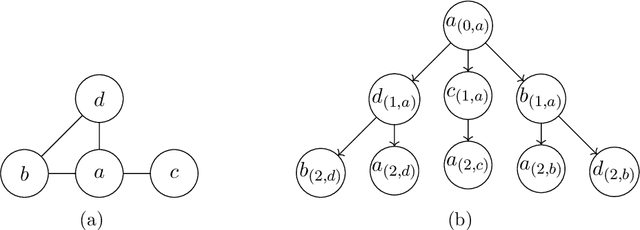
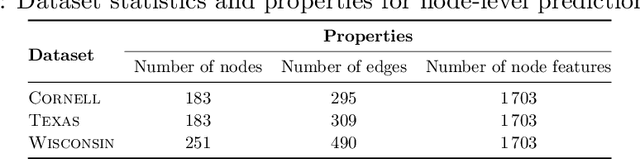
While (message-passing) graph neural networks have clear limitations in approximating permutation-equivariant functions over graphs or general relational data, more expressive, higher-order graph neural networks do not scale to large graphs. They either operate on $k$-order tensors or consider all $k$-node subgraphs, implying an exponential dependence on $k$ in memory requirements, and do not adapt to the sparsity of the graph. By introducing new heuristics for the graph isomorphism problem, we devise a class of universal, permutation-equivariant graph networks, which, unlike previous architectures, offer a fine-grained control between expressivity and scalability and adapt to the sparsity of the graph. These architectures lead to vastly reduced computation times compared to standard higher-order graph networks in the supervised node- and graph-level classification and regression regime while significantly improving over standard graph neural network and graph kernel architectures in terms of predictive performance.