Untangling Gaussian Mixtures

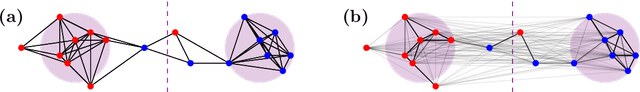
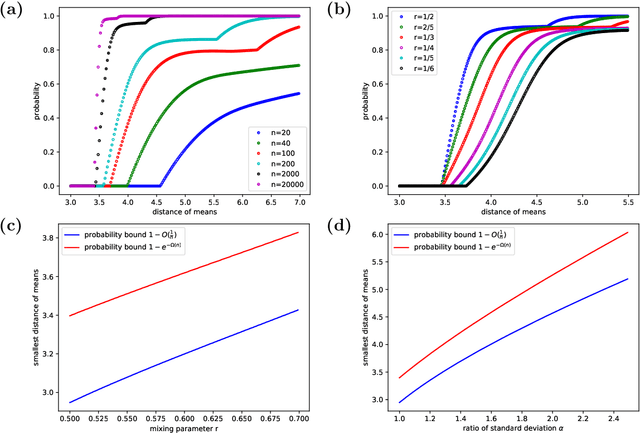
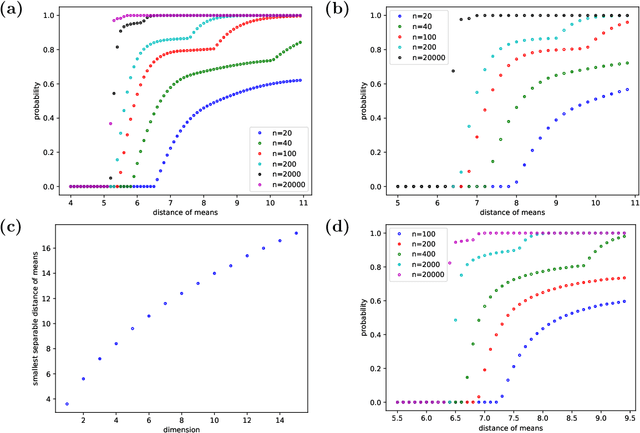
Tangles were originally introduced as a concept to formalize regions of high connectivity in graphs. In recent years, they have also been discovered as a link between structural graph theory and data science: when interpreting similarity in data sets as connectivity between points, finding clusters in the data essentially amounts to finding tangles in the underlying graphs. This paper further explores the potential of tangles in data sets as a means for a formal study of clusters. Real-world data often follow a normal distribution. Accounting for this, we develop a quantitative theory of tangles in data sets drawn from Gaussian mixtures. To this end, we equip the data with a graph structure that models similarity between the points and allows us to apply tangle theory to the data. We provide explicit conditions under which tangles associated with the marginal Gaussian distributions exist asymptotically almost surely. This can be considered as a sufficient formal criterion for the separabability of clusters in the data.

SpeqNets: Sparsity-aware Permutation-equivariant Graph Networks

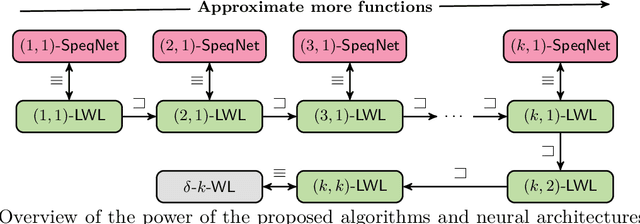
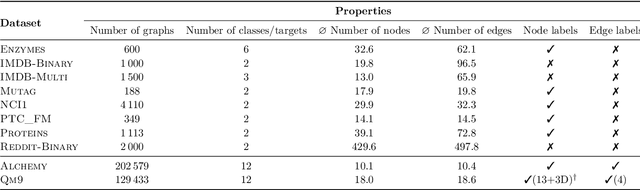
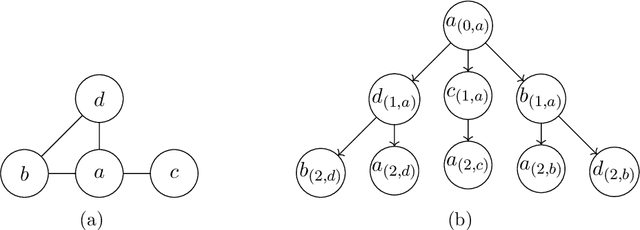
While (message-passing) graph neural networks have clear limitations in approximating permutation-equivariant functions over graphs or general relational data, more expressive, higher-order graph neural networks do not scale to large graphs. They either operate on $k$-order tensors or consider all $k$-node subgraphs, implying an exponential dependence on $k$ in memory requirements, and do not adapt to the sparsity of the graph. By introducing new heuristics for the graph isomorphism problem, we devise a class of universal, permutation-equivariant graph networks, which, unlike previous architectures, offer a fine-grained control between expressivity and scalability and adapt to the sparsity of the graph. These architectures lead to vastly reduced computation times compared to standard higher-order graph networks in the supervised node- and graph-level classification and regression regime while significantly improving over standard graph neural network and graph kernel architectures in terms of predictive performance.