Eva Fluck
Untangling Gaussian Mixtures
Mar 11, 2024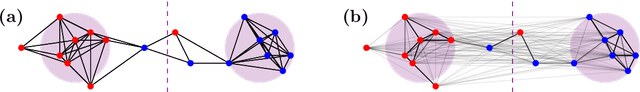
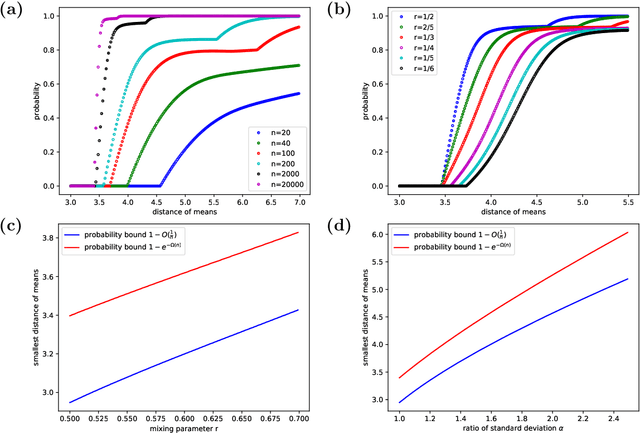

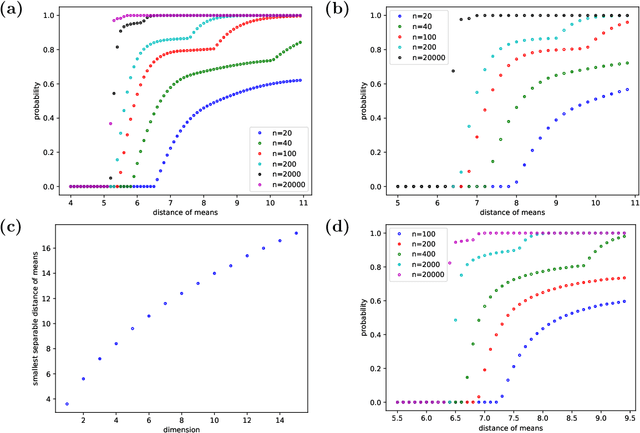
Abstract:Tangles were originally introduced as a concept to formalize regions of high connectivity in graphs. In recent years, they have also been discovered as a link between structural graph theory and data science: when interpreting similarity in data sets as connectivity between points, finding clusters in the data essentially amounts to finding tangles in the underlying graphs. This paper further explores the potential of tangles in data sets as a means for a formal study of clusters. Real-world data often follow a normal distribution. Accounting for this, we develop a quantitative theory of tangles in data sets drawn from Gaussian mixtures. To this end, we equip the data with a graph structure that models similarity between the points and allows us to apply tangle theory to the data. We provide explicit conditions under which tangles associated with the marginal Gaussian distributions exist asymptotically almost surely. This can be considered as a sufficient formal criterion for the separabability of clusters in the data.
Tangles and Hierarchical Clustering
Mar 16, 2022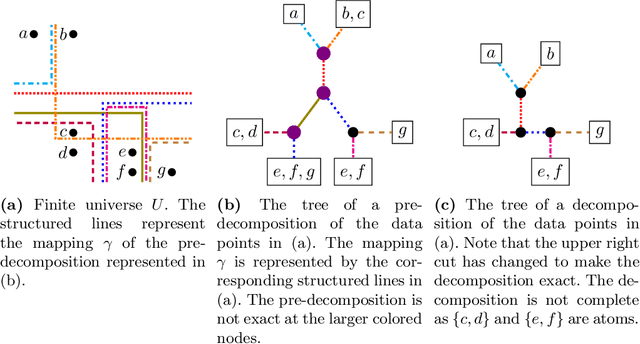
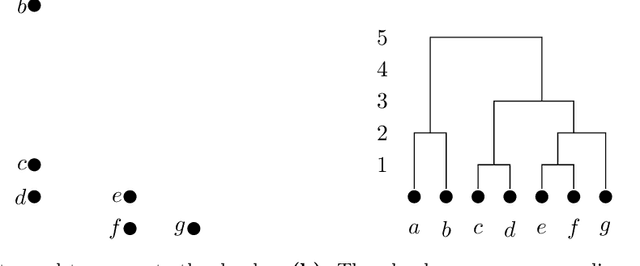
Abstract:We establish a connection between tangles, a concept from structural graph theory that plays a central role in Robertson and Seymour's graph minor project, and hierarchical clustering. Tangles cannot only be defined for graphs, but in fact for arbitrary connectivity functions, which are functions defined on the subsets of some finite universe. In typical clustering applications these universes consist of points in some metric space. Connectivity functions are usually required to be submodular. It is our first contribution to show that the central duality theorem connecting tangles with hierarchical decompositions (so-called branch decompositions) also holds if submodularity is replaced by a different property that we call maximum-submodular. We then define a connectivity function on finite data sets in an arbitrary metric space and prove that its tangles are in one-to-one correspondence with the clusters obtained by applying the well-known single linkage clustering algorithms to the same data set. Lastly we generalize this correspondence for any hierarchical clustering. We show that the data structure that represents hierarchical clustering results, called dendograms, are equivalent to maximum-submodular connectivity functions and their tangles. The idea of viewing tangles as clusters has first been proposed by Diestel and Whittle in 2016 as an approach to image segmentation. To the best of our knowledge, our result is the first that establishes a precise technical connection between tangles and clusters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge