Tangles and Hierarchical Clustering
Paper and Code
Mar 16, 2022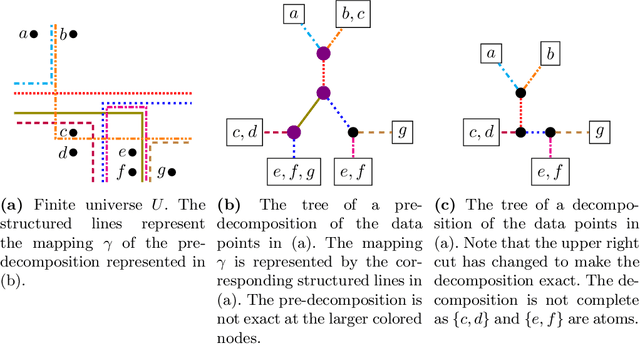
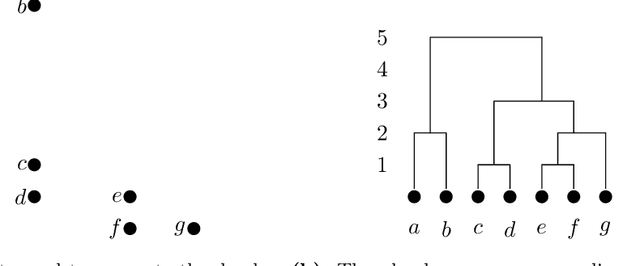
We establish a connection between tangles, a concept from structural graph theory that plays a central role in Robertson and Seymour's graph minor project, and hierarchical clustering. Tangles cannot only be defined for graphs, but in fact for arbitrary connectivity functions, which are functions defined on the subsets of some finite universe. In typical clustering applications these universes consist of points in some metric space. Connectivity functions are usually required to be submodular. It is our first contribution to show that the central duality theorem connecting tangles with hierarchical decompositions (so-called branch decompositions) also holds if submodularity is replaced by a different property that we call maximum-submodular. We then define a connectivity function on finite data sets in an arbitrary metric space and prove that its tangles are in one-to-one correspondence with the clusters obtained by applying the well-known single linkage clustering algorithms to the same data set. Lastly we generalize this correspondence for any hierarchical clustering. We show that the data structure that represents hierarchical clustering results, called dendograms, are equivalent to maximum-submodular connectivity functions and their tangles. The idea of viewing tangles as clusters has first been proposed by Diestel and Whittle in 2016 as an approach to image segmentation. To the best of our knowledge, our result is the first that establishes a precise technical connection between tangles and clusters.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge