Orbitopal Fixing in SAT

Despite their sophisticated heuristics, boolean satisfiability (SAT) solvers are still vulnerable to symmetry, causing them to visit search regions that are symmetric to ones already explored. While symmetry handling is routine in other solving paradigms, integrating it into state-of-the-art proof-producing SAT solvers is difficult: added reasoning must be fast, non-interfering with solver heuristics, and compatible with formal proof logging. To address these issues, we present a practical static symmetry breaking approach based on orbitopal fixing, a technique adapted from mixed-integer programming. Our approach adds only unit clauses, which minimizes downstream slowdowns, and it emits succinct proof certificates in the substitution redundancy proof system. Implemented in the satsuma tool, our methods deliver consistent speedups on symmetry-rich benchmarks with negligible regressions elsewhere.

The Complexity of Symmetry Breaking Beyond Lex-Leader

Symmetry breaking is a widely popular approach to enhance solvers in constraint programming, such as those for SAT or MIP. Symmetry breaking predicates (SBPs) typically impose an order on variables and single out the lexicographic leader (lex-leader) in each orbit of assignments. Although it is NP-hard to find complete lex-leader SBPs, incomplete lex-leader SBPs are widely used in practice. In this paper, we investigate the complexity of computing complete SBPs, lex-leader or otherwise, for SAT. Our main result proves a natural barrier for efficiently computing SBPs: efficient certification of graph non-isomorphism. Our results explain the difficulty of obtaining short SBPs for important CP problems, such as matrix-models with row-column symmetries and graph generation problems. Our results hold even when SBPs are allowed to introduce additional variables. We show polynomial upper bounds for breaking certain symmetry groups, namely automorphism groups of trees and wreath products of groups with efficient SBPs.

Trainability for Universal GNNs Through Surgical Randomness

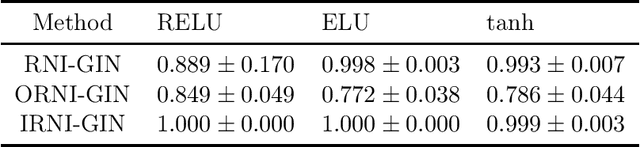
Message passing neural networks (MPNN) have provable limitations, which can be overcome by universal networks. However, universal networks are typically impractical. The only exception is random node initialization (RNI), a data augmentation method that results in provably universal networks. Unfortunately, RNI suffers from severe drawbacks such as slow convergence and high sensitivity to changes in hyperparameters. We transfer powerful techniques from the practical world of graph isomorphism testing to MPNNs, resolving these drawbacks. This culminates in individualization-refinement node initialization (IRNI). We replace the indiscriminate and haphazard randomness used in RNI by a surgical incision of only a few random bits at well-selected nodes. Our novel non-intrusive data-augmentation scheme maintains the networks' universality while resolving the trainability issues. We formally prove the claimed universality and corroborate experimentally -- on synthetic benchmarks sets previously explicitly designed for that purpose -- that IRNI overcomes the limitations of MPNNs. We also verify the practical efficacy of our approach on the standard benchmark data sets PROTEINS and NCI1.