Semantic Probabilistic Control of Language Models

Semantic control entails steering LM generations towards satisfying subtle non-lexical constraints, e.g., toxicity, sentiment, or politeness, attributes that can be captured by a sequence-level verifier. It can thus be viewed as sampling from the LM distribution conditioned on the target attribute, a computationally intractable problem due to the non-decomposable nature of the verifier. Existing approaches to LM control either only deal with syntactic constraints which cannot capture the aforementioned attributes, or rely on sampling to explore the conditional LM distribution, an ineffective estimator for low-probability events. In this work, we leverage a verifier's gradient information to efficiently reason over all generations that satisfy the target attribute, enabling precise steering of LM generations by reweighing the next-token distribution. Starting from an initial sample, we create a local LM distribution favoring semantically similar sentences. This approximation enables the tractable computation of an expected sentence embedding. We use this expected embedding, informed by the verifier's evaluation at the initial sample, to estimate the probability of satisfying the constraint, which directly informs the update to the next-token distribution. We evaluated the effectiveness of our approach in controlling the toxicity, sentiment, and topic-adherence of LMs yielding generations satisfying the constraint with high probability (>95%) without degrading their quality.

Controllable Generation via Locally Constrained Resampling

Autoregressive models have demonstrated an unprecedented ability at modeling the intricacies of natural language. However, they continue to struggle with generating complex outputs that adhere to logical constraints. Sampling from a fully-independent distribution subject to a constraint is hard. Sampling from an autoregressive distribution subject to a constraint is doubly hard: We have to contend not only with the hardness of the constraint but also the distribution's lack of structure. We propose a tractable probabilistic approach that performs Bayesian conditioning to draw samples subject to a constraint. Our approach considers the entire sequence, leading to a more globally optimal constrained generation than current greedy methods. Starting from a model sample, we induce a local, factorized distribution which we can tractably condition on the constraint. To generate samples that satisfy the constraint, we sample from the conditional distribution, correct for biases in the samples and resample. The resulting samples closely approximate the target distribution and are guaranteed to satisfy the constraints. We evaluate our approach on several tasks, including LLM detoxification and solving Sudoku puzzles. We show that by disallowing a list of toxic expressions our approach is able to steer the model's outputs away from toxic generations, outperforming similar approaches to detoxification. We conclude by showing that our approach achieves a perfect accuracy on Sudoku compared to <50% for GPT4-o and Gemini 1.5.

Where is the signal in tokenization space?

Large Language Models (LLMs) are typically shipped with tokenizers that deterministically encode text into so-called canonical token sequences, to which the LLMs assign probability values. One common assumption is that the probability of a piece of text is the probability of its canonical token sequence. However, the tokenization of a string is not unique: e.g., the Llama2 tokenizer encodes Tokens as [Tok,ens], but [Tok,en,s] also represents the same text. In this paper, we study non-canonical tokenizations. We prove that, given a string, it is computationally hard to find the most likely tokenization for an autoregressive LLM, as well as to compute the marginal probability over all possible tokenizations. We then show how the marginal is, in most cases, indistinguishable from the canonical probability. Surprisingly, we then empirically demonstrate the existence of a significant amount of signal hidden within tokenization space. Notably, by simply aggregating the probabilities of non-canonical tokenizations, we achieve improvements across a range of LLM evaluation benchmarks for a variety of architectures, including transformers and state space models.

Scaling Tractable Probabilistic Circuits: A Systems Perspective

Probabilistic Circuits (PCs) are a general framework for tractable deep generative models, which support exact and efficient probabilistic inference on their learned distributions. Recent modeling and training advancements have enabled their application to complex real-world tasks. However, the time and memory inefficiency of existing PC implementations hinders further scaling up. This paper proposes PyJuice, a general GPU implementation design for PCs that improves prior art in several regards. Specifically, PyJuice is 1-2 orders of magnitude faster than existing systems (including very recent ones) at training large-scale PCs. Moreover, PyJuice consumes 2-5x less GPU memory, which enables us to train larger models. At the core of our system is a compilation process that converts a PC into a compact representation amenable to efficient block-based parallelization, which significantly reduces IO and makes it possible to leverage Tensor Cores available in modern GPUs. Empirically, PyJuice can be used to improve state-of-the-art PCs trained on image (e.g., ImageNet32) and language (e.g., WikiText, CommonGen) datasets. We further establish a new set of baselines on natural image and language datasets by benchmarking existing PC structures but with much larger sizes and more training epochs, with the hope of incentivizing future research. Code is available at https://github.com/Tractables/pyjuice.

Semantic Loss Functions for Neuro-Symbolic Structured Prediction

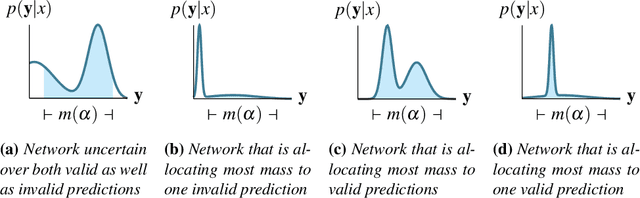
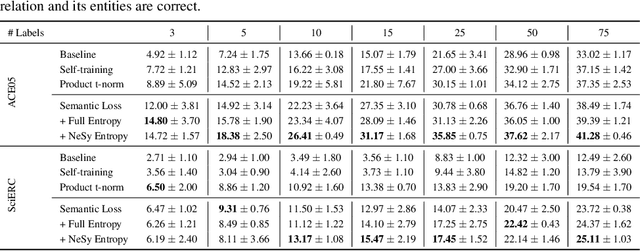
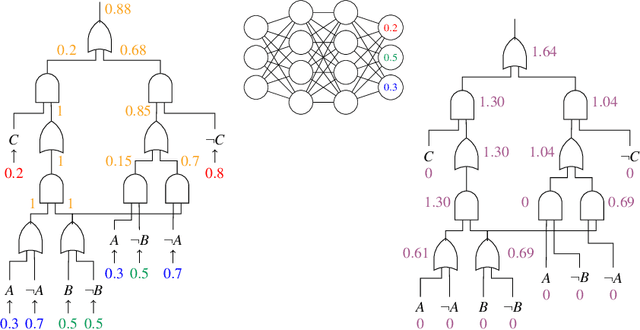
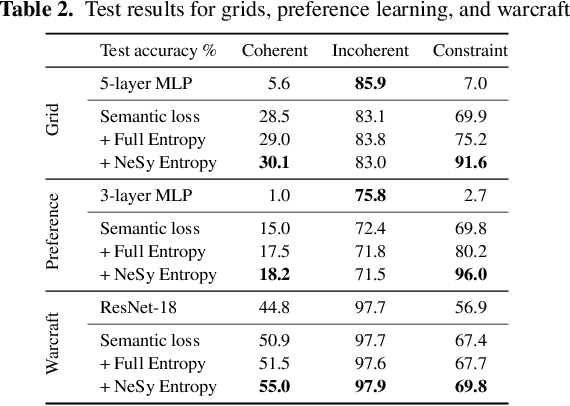
Structured output prediction problems are ubiquitous in machine learning. The prominent approach leverages neural networks as powerful feature extractors, otherwise assuming the independence of the outputs. These outputs, however, jointly encode an object, e.g. a path in a graph, and are therefore related through the structure underlying the output space. We discuss the semantic loss, which injects knowledge about such structure, defined symbolically, into training by minimizing the network's violation of such dependencies, steering the network towards predicting distributions satisfying the underlying structure. At the same time, it is agnostic to the arrangement of the symbols, and depends only on the semantics expressed thereby, while also enabling efficient end-to-end training and inference. We also discuss key improvements and applications of the semantic loss. One limitations of the semantic loss is that it does not exploit the association of every data point with certain features certifying its membership in a target class. We should therefore prefer minimum-entropy distributions over valid structures, which we obtain by additionally minimizing the neuro-symbolic entropy. We empirically demonstrate the benefits of this more refined formulation. Moreover, the semantic loss is designed to be modular and can be combined with both discriminative and generative neural models. This is illustrated by integrating it into generative adversarial networks, yielding constrained adversarial networks, a novel class of deep generative models able to efficiently synthesize complex objects obeying the structure of the underlying domain.

A Pseudo-Semantic Loss for Autoregressive Models with Logical Constraints

Neuro-symbolic AI bridges the gap between purely symbolic and neural approaches to learning. This often requires maximizing the likelihood of a symbolic constraint w.r.t the neural network's output distribution. Such output distributions are typically assumed to be fully-factorized. This limits the applicability of neuro-symbolic learning to the more expressive autoregressive distributions, e.g., transformers. Under such distributions, computing the likelihood of even simple constraints is #P-hard. Instead of attempting to enforce the constraint on the entire output distribution, we propose to do so on a random, local approximation thereof. More precisely, we optimize the likelihood of the constraint under a pseudolikelihood-based approximation centered around a model sample. Our approximation is factorized, allowing the reuse of solutions to sub-problems, a main tenet for efficiently computing neuro-symbolic losses. Moreover, it is a local, high-fidelity approximation of the likelihood, exhibiting low entropy and KL-divergence around the model sample. We evaluate our approach on Sudoku and shortest-path prediction cast as autoregressive generation, and observe that we greatly improve upon the base model's ability to predict logically-consistent outputs. We also evaluate on the task of detoxifying large language models. Using a simple constraint disallowing a list of toxic words, we are able to steer the model's outputs away from toxic generations, achieving SoTA detoxification compared to previous approaches.

A Unified Approach to Count-Based Weakly-Supervised Learning

High-quality labels are often very scarce, whereas unlabeled data with inferred weak labels occurs more naturally. In many cases, these weak labels dictate the frequency of each respective class over a set of instances. In this paper, we develop a unified approach to learning from such weakly-labeled data, which we call count-based weakly-supervised learning. At the heart of our approach is the ability to compute the probability of exactly k out of n outputs being set to true. This computation is differentiable, exact, and efficient. Building upon the previous computation, we derive a count loss penalizing the model for deviations in its distribution from an arithmetic constraint defined over label counts. We evaluate our approach on three common weakly-supervised learning paradigms and observe that our proposed approach achieves state-of-the-art or highly competitive results across all three of the paradigms.

Probabilistically Rewired Message-Passing Neural Networks

Message-passing graph neural networks (MPNNs) emerged as powerful tools for processing graph-structured input. However, they operate on a fixed input graph structure, ignoring potential noise and missing information. Furthermore, their local aggregation mechanism can lead to problems such as over-squashing and limited expressive power in capturing relevant graph structures. Existing solutions to these challenges have primarily relied on heuristic methods, often disregarding the underlying data distribution. Hence, devising principled approaches for learning to infer graph structures relevant to the given prediction task remains an open challenge. In this work, leveraging recent progress in exact and differentiable $k$-subset sampling, we devise probabilistically rewired MPNNs (PR-MPNNs), which learn to add relevant edges while omitting less beneficial ones. For the first time, our theoretical analysis explores how PR-MPNNs enhance expressive power, and we identify precise conditions under which they outperform purely randomized approaches. Empirically, we demonstrate that our approach effectively mitigates issues like over-squashing and under-reaching. In addition, on established real-world datasets, our method exhibits competitive or superior predictive performance compared to traditional MPNN models and recent graph transformer architectures.

Semantic Strengthening of Neuro-Symbolic Learning

Numerous neuro-symbolic approaches have recently been proposed typically with the goal of adding symbolic knowledge to the output layer of a neural network. Ideally, such losses maximize the probability that the neural network's predictions satisfy the underlying domain. Unfortunately, this type of probabilistic inference is often computationally infeasible. Neuro-symbolic approaches therefore commonly resort to fuzzy approximations of this probabilistic objective, sacrificing sound probabilistic semantics, or to sampling which is very seldom feasible. We approach the problem by first assuming the constraint decomposes conditioned on the features learned by the network. We iteratively strengthen our approximation, restoring the dependence between the constraints most responsible for degrading the quality of the approximation. This corresponds to computing the mutual information between pairs of constraints conditioned on the network's learned features, and may be construed as a measure of how well aligned the gradients of two distributions are. We show how to compute this efficiently for tractable circuits. We test our approach on three tasks: predicting a minimum-cost path in Warcraft, predicting a minimum-cost perfect matching, and solving Sudoku puzzles, observing that it improves upon the baselines while sidestepping intractability.

SIMPLE: A Gradient Estimator for $k$-Subset Sampling

$k$-subset sampling is ubiquitous in machine learning, enabling regularization and interpretability through sparsity. The challenge lies in rendering $k$-subset sampling amenable to end-to-end learning. This has typically involved relaxing the reparameterized samples to allow for backpropagation, with the risk of introducing high bias and high variance. In this work, we fall back to discrete $k$-subset sampling on the forward pass. This is coupled with using the gradient with respect to the exact marginals, computed efficiently, as a proxy for the true gradient. We show that our gradient estimator, SIMPLE, exhibits lower bias and variance compared to state-of-the-art estimators, including the straight-through Gumbel estimator when $k = 1$. Empirical results show improved performance on learning to explain and sparse linear regression. We provide an algorithm for computing the exact ELBO for the $k$-subset distribution, obtaining significantly lower loss compared to SOTA.