Lizeth Gonzalez-Carabarin
Dynamic Probabilistic Pruning: A general framework for hardware-constrained pruning at different granularities
May 26, 2021

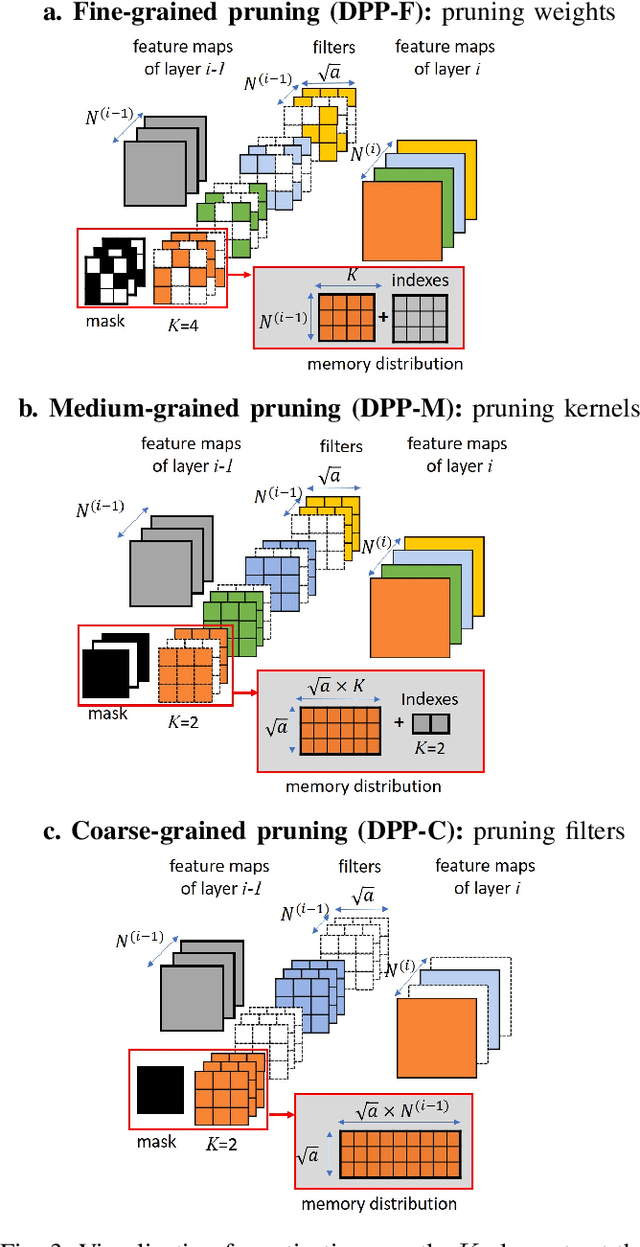
Abstract:Unstructured neural network pruning algorithms have achieved impressive compression rates. However, the resulting - typically irregular - sparse matrices hamper efficient hardware implementations, leading to additional memory usage and complex control logic that diminishes the benefits of unstructured pruning. This has spurred structured coarse-grained pruning solutions that prune entire filters or even layers, enabling efficient implementation at the expense of reduced flexibility. Here we propose a flexible new pruning mechanism that facilitates pruning at different granularities (weights, kernels, filters/feature maps), while retaining efficient memory organization (e.g. pruning exactly k-out-of-n weights for every output neuron, or pruning exactly k-out-of-n kernels for every feature map). We refer to this algorithm as Dynamic Probabilistic Pruning (DPP). DPP leverages the Gumbel-softmax relaxation for differentiable k-out-of-n sampling, facilitating end-to-end optimization. We show that DPP achieves competitive compression rates and classification accuracy when pruning common deep learning models trained on different benchmark datasets for image classification. Relevantly, the non-magnitude-based nature of DPP allows for joint optimization of pruning and weight quantization in order to even further compress the network, which we show as well. Finally, we propose novel information theoretic metrics that show the confidence and pruning diversity of pruning masks within a layer.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge