EconEvals: Benchmarks and Litmus Tests for LLM Agents in Unknown Environments

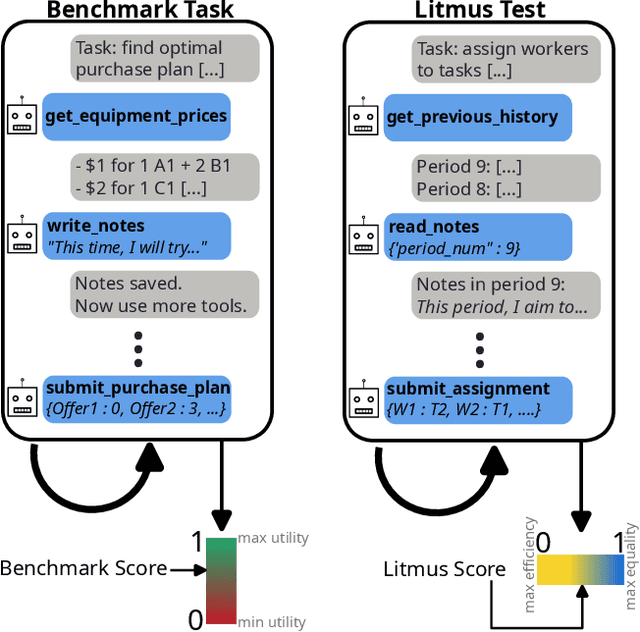
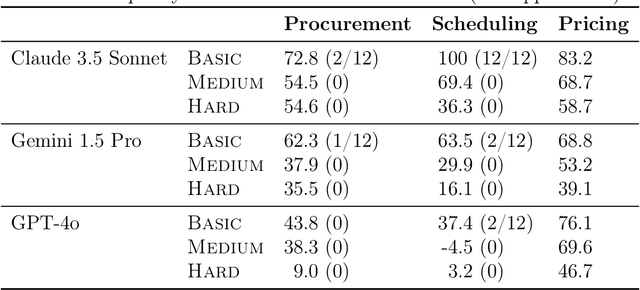
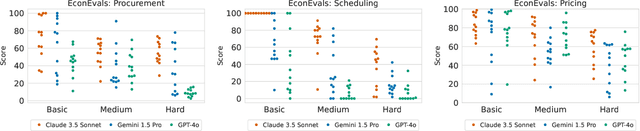
We develop benchmarks for LLM agents that act in, learn from, and strategize in unknown environments, the specifications of which the LLM agent must learn over time from deliberate exploration. Our benchmarks consist of decision-making tasks derived from key problems in economics. To forestall saturation, the benchmark tasks are synthetically generated with scalable difficulty levels. Additionally, we propose litmus tests, a new kind of quantitative measure for LLMs and LLM agents. Unlike benchmarks, litmus tests quantify differences in character, values, and tendencies of LLMs and LLM agents, by considering their behavior when faced with tradeoffs (e.g., efficiency versus equality) where there is no objectively right or wrong behavior. Overall, our benchmarks and litmus tests assess the abilities and tendencies of LLM agents in tackling complex economic problems in diverse settings spanning procurement, scheduling, task allocation, and pricing -- applications that should grow in importance as such agents are further integrated into the economy.

Algorithmic Collusion by Large Language Models

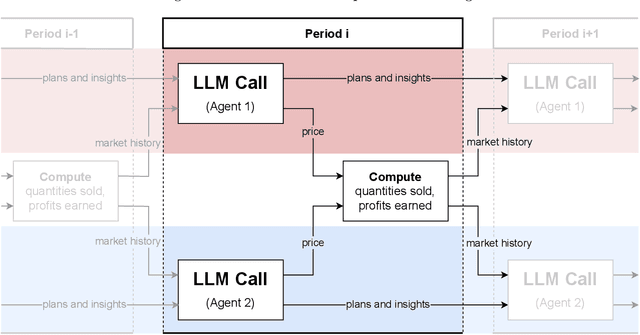
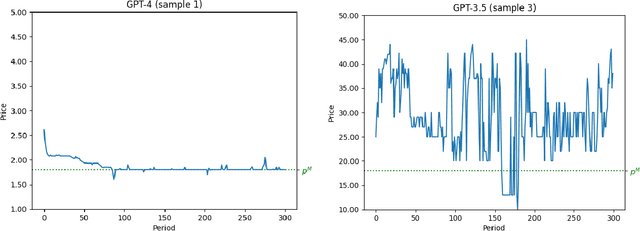
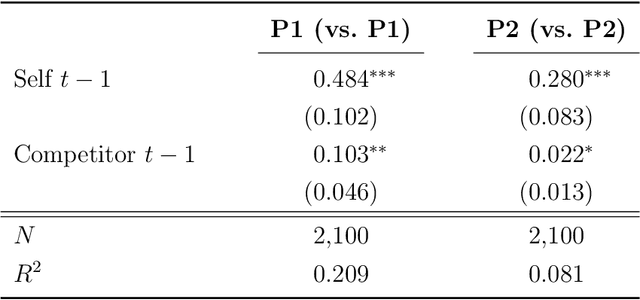
The rise of algorithmic pricing raises concerns of algorithmic collusion. We conduct experiments with algorithmic pricing agents based on Large Language Models (LLMs), and specifically GPT-4. We find that (1) LLM-based agents are adept at pricing tasks, (2) LLM-based pricing agents autonomously collude in oligopoly settings to the detriment of consumers, and (3) variation in seemingly innocuous phrases in LLM instructions ("prompts") may increase collusion. These results extend to auction settings. Our findings underscore the need for antitrust regulation regarding algorithmic pricing, and uncover regulatory challenges unique to LLM-based pricing agents.

The Distortion of Binomial Voting Defies Expectation

In computational social choice, the distortion of a voting rule quantifies the degree to which the rule overcomes limited preference information to select a socially desirable outcome. This concept has been investigated extensively, but only through a worst-case lens. Instead, we study the expected distortion of voting rules with respect to an underlying distribution over voter utilities. Our main contribution is the design and analysis of a novel and intuitive rule, binomial voting, which provides strong expected distortion guarantees for all distributions.

The Complexity of Interactively Learning a Stable Matching by Trial and Error

In a stable matching setting, we consider a query model that allows for an interactive learning algorithm to make precisely one type of query: proposing a matching, the response to which is either that the proposed matching is stable, or a blocking pair (chosen adversarially) indicating that this matching is unstable. For one-to-one matching markets, our main result is an essentially tight upper bound of $O(n^2\log n)$ on the deterministic query complexity of interactively learning a stable matching in this coarse query model, along with an efficient randomized algorithm that achieves this query complexity with high probability. For many-to-many matching markets in which participants have responsive preferences, we first give an interactive learning algorithm whose query complexity and running time are polynomial in the size of the market if the maximum quota of each agent is bounded; our main result for many-to-many markets is that the deterministic query complexity can be made polynomial (more specifically, $O(n^3 \log n)$) in the size of the market even for arbitrary (e.g., linear in the market size) quotas.

The Sample Complexity of Up-to-$\varepsilon$ Multi-Dimensional Revenue Maximization

We consider the sample complexity of revenue maximization for multiple bidders in unrestricted multi-dimensional settings. Specifically, we study the standard model of $n$ additive bidders whose values for $m$ heterogeneous items are drawn independently. For any such instance and any $\varepsilon>0$, we show that it is possible to learn an $\varepsilon$-Bayesian Incentive Compatible auction whose expected revenue is within $\varepsilon$ of the optimal $\varepsilon$-BIC auction from only polynomially many samples. Our approach is based on ideas that hold quite generally, and completely sidestep the difficulty of characterizing optimal (or near-optimal) auctions for these settings. Therefore, our results easily extend to general multi-dimensional settings, including valuations that aren't necessarily even subadditive, and arbitrary allocation constraints. For the cases of a single bidder and many goods, or a single parameter (good) and many bidders, our analysis yields exact incentive compatibility (and for the latter also computational efficiency). Although the single-parameter case is already well-understood, our corollary for this case extends slightly the state-of-the-art.

Submultiplicative Glivenko-Cantelli and Uniform Convergence of Revenues

In this work we derive a variant of the classic Glivenko-Cantelli Theorem, which asserts uniform convergence of the empirical Cumulative Distribution Function (CDF) to the CDF of the underlying distribution. Our variant allows for tighter convergence bounds for extreme values of the CDF. We apply our bound in the context of revenue learning, which is a well-studied problem in economics and algorithmic game theory. We derive sample-complexity bounds on the uniform convergence rate of the empirical revenues to the true revenues, assuming a bound on the $k$th moment of the valuations, for any (possibly fractional) $k>1$. For uniform convergence in the limit, we give a complete characterization and a zero-one law: if the first moment of the valuations is finite, then uniform convergence almost surely occurs; conversely, if the first moment is infinite, then uniform convergence almost never occurs.