Eylon Yogev
Adversarial Laws of Large Numbers and Optimal Regret in Online Classification
Jan 22, 2021
Abstract:Laws of large numbers guarantee that given a large enough sample from some population, the measure of any fixed sub-population is well-estimated by its frequency in the sample. We study laws of large numbers in sampling processes that can affect the environment they are acting upon and interact with it. Specifically, we consider the sequential sampling model proposed by Ben-Eliezer and Yogev (2020), and characterize the classes which admit a uniform law of large numbers in this model: these are exactly the classes that are \emph{online learnable}. Our characterization may be interpreted as an online analogue to the equivalence between learnability and uniform convergence in statistical (PAC) learning. The sample-complexity bounds we obtain are tight for many parameter regimes, and as an application, we determine the optimal regret bounds in online learning, stated in terms of \emph{Littlestone's dimension}, thus resolving the main open question from Ben-David, P\'al, and Shalev-Shwartz (2009), which was also posed by Rakhlin, Sridharan, and Tewari (2015).
The Deep Journey from Content to Collaborative Filtering
Nov 01, 2016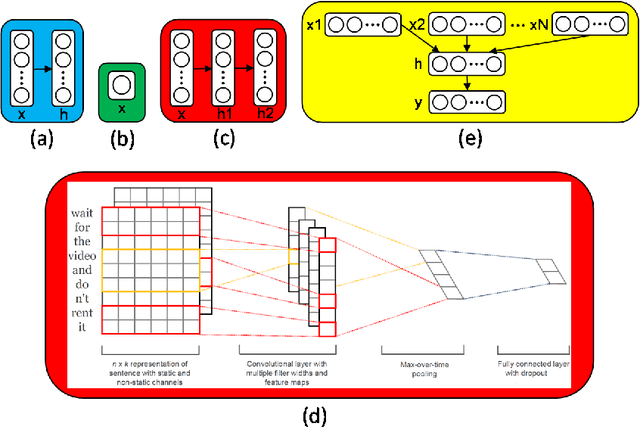
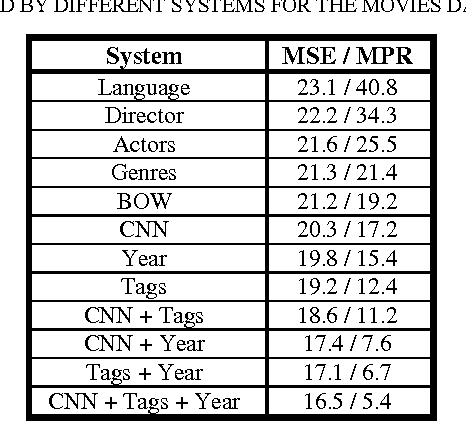

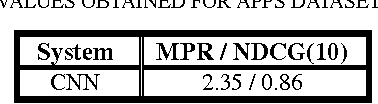
Abstract:In Recommender Systems research, algorithms are often characterized as either Collaborative Filtering (CF) or Content Based (CB). CF algorithms are trained using a dataset of user explicit or implicit preferences while CB algorithms are typically based on item profiles. These approaches harness very different data sources hence the resulting recommended items are generally also very different. This paper presents a novel model that serves as a bridge from items content into their CF representations. We introduce a multiple input deep regression model to predict the CF latent embedding vectors of items based on their textual description and metadata. We showcase the effectiveness of the proposed model by predicting the CF vectors of movies and apps based on their textual descriptions. Finally, we show that the model can be further improved by incorporating metadata such as the movie release year and tags which contribute to a higher accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge