Active Learning Polynomial Threshold Functions

We initiate the study of active learning polynomial threshold functions (PTFs). While traditional lower bounds imply that even univariate quadratics cannot be non-trivially actively learned, we show that allowing the learner basic access to the derivatives of the underlying classifier circumvents this issue and leads to a computationally efficient algorithm for active learning degree-$d$ univariate PTFs in $\tilde{O}(d^3\log(1/\varepsilon\delta))$ queries. We also provide near-optimal algorithms and analyses for active learning PTFs in several average case settings. Finally, we prove that access to derivatives is insufficient for active learning multivariate PTFs, even those of just two variables.

What is Learned in Knowledge Graph Embeddings?

A knowledge graph (KG) is a data structure which represents entities and relations as the vertices and edges of a directed graph with edge types. KGs are an important primitive in modern machine learning and artificial intelligence. Embedding-based models, such as the seminal TransE [Bordes et al., 2013] and the recent PairRE [Chao et al., 2020] are among the most popular and successful approaches for representing KGs and inferring missing edges (link completion). Their relative success is often credited in the literature to their ability to learn logical rules between the relations. In this work, we investigate whether learning rules between relations is indeed what drives the performance of embedding-based methods. We define motif learning and two alternative mechanisms, network learning (based only on the connectivity of the KG, ignoring the relation types), and unstructured statistical learning (ignoring the connectivity of the graph). Using experiments on synthetic KGs, we show that KG models can learn motifs and how this ability is degraded by non-motif (noise) edges. We propose tests to distinguish the contributions of the three mechanisms to performance, and apply them to popular KG benchmarks. We also discuss an issue with the standard performance testing protocol and suggest an improvement. To appear in the proceedings of Complex Networks 2021.

Learning Multimodal Affinities for Textual Editing in Images

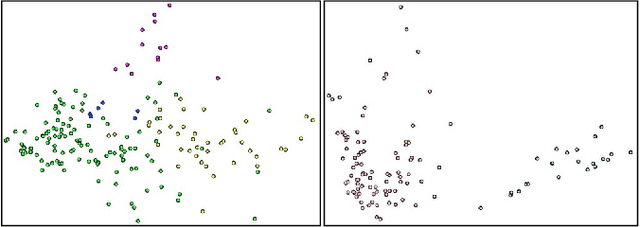
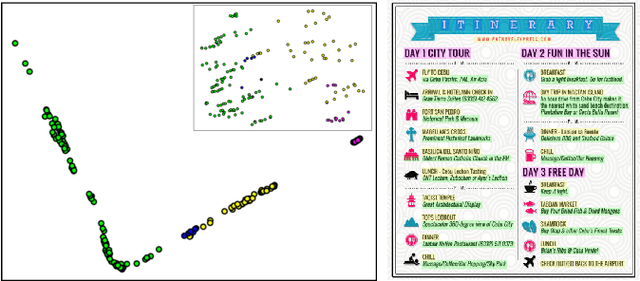
Nowadays, as cameras are rapidly adopted in our daily routine, images of documents are becoming both abundant and prevalent. Unlike natural images that capture physical objects, document-images contain a significant amount of text with critical semantics and complicated layouts. In this work, we devise a generic unsupervised technique to learn multimodal affinities between textual entities in a document-image, considering their visual style, the content of their underlying text and their geometric context within the image. We then use these learned affinities to automatically cluster the textual entities in the image into different semantic groups. The core of our approach is a deep optimization scheme dedicated for an image provided by the user that detects and leverages reliable pairwise connections in the multimodal representation of the textual elements in order to properly learn the affinities. We show that our technique can operate on highly varying images spanning a wide range of documents and demonstrate its applicability for various editing operations manipulating the content, appearance and geometry of the image.

Adversarial Laws of Large Numbers and Optimal Regret in Online Classification

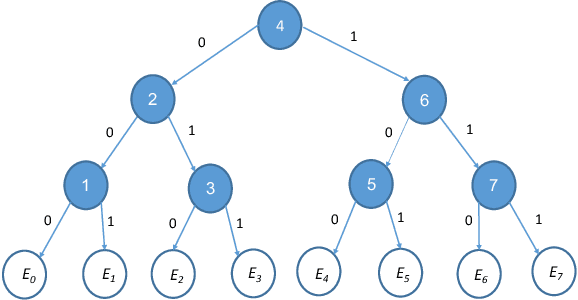
Laws of large numbers guarantee that given a large enough sample from some population, the measure of any fixed sub-population is well-estimated by its frequency in the sample. We study laws of large numbers in sampling processes that can affect the environment they are acting upon and interact with it. Specifically, we consider the sequential sampling model proposed by Ben-Eliezer and Yogev (2020), and characterize the classes which admit a uniform law of large numbers in this model: these are exactly the classes that are \emph{online learnable}. Our characterization may be interpreted as an online analogue to the equivalence between learnability and uniform convergence in statistical (PAC) learning. The sample-complexity bounds we obtain are tight for many parameter regimes, and as an application, we determine the optimal regret bounds in online learning, stated in terms of \emph{Littlestone's dimension}, thus resolving the main open question from Ben-David, P\'al, and Shalev-Shwartz (2009), which was also posed by Rakhlin, Sridharan, and Tewari (2015).

READ: Recursive Autoencoders for Document Layout Generation

Layout is a fundamental component of any graphic design. Creating large varieties of plausible document layouts can be a tedious task, requiring numerous constraints to be satisfied, including local ones relating different semantic elements and global constraints on the general appearance and spacing. In this paper, we present a novel framework, coined READ, for REcursive Autoencoders for Document layout generation, to generate plausible 2D layouts of documents in large quantities and varieties. First, we devise an exploratory recursive method to extract a structural decomposition of a single document. Leveraging a dataset of documents annotated with labeled bounding boxes, our recursive neural network learns to map the structural representation, given in the form of a simple hierarchy, to a compact code, the space of which is approximated by a Gaussian distribution. Novel hierarchies can be sampled from this space, obtaining new document layouts. Moreover, we introduce a combinatorial metric to measure structural similarity among document layouts. We deploy it to show that our method is able to generate highly variable and realistic layouts. We further demonstrate the utility of our generated layouts in the context of standard detection tasks on documents, showing that detection performance improves when the training data is augmented with generated documents whose layouts are produced by READ.

Deleting and Testing Forbidden Patterns in Multi-Dimensional Arrays

Understanding the local behaviour of structured multi-dimensional data is a fundamental problem in various areas of computer science. As the amount of data is often huge, it is desirable to obtain sublinear time algorithms, and specifically property testers, to understand local properties of the data. We focus on the natural local problem of testing pattern freeness: given a large $d$-dimensional array $A$ and a fixed $d$-dimensional pattern $P$ over a finite alphabet, we say that $A$ is $P$-free if it does not contain a copy of the forbidden pattern $P$ as a consecutive subarray. The distance of $A$ to $P$-freeness is the fraction of entries of $A$ that need to be modified to make it $P$-free. For any $\epsilon \in [0,1]$ and any large enough pattern $P$ over any alphabet, other than a very small set of exceptional patterns, we design a tolerant tester that distinguishes between the case that the distance is at least $\epsilon$ and the case that it is at most $a_d \epsilon$, with query complexity and running time $c_d \epsilon^{-1}$, where $a_d < 1$ and $c_d$ depend only on $d$. To analyze the testers we establish several combinatorial results, including the following $d$-dimensional modification lemma, which might be of independent interest: for any large enough pattern $P$ over any alphabet (excluding a small set of exceptional patterns for the binary case), and any array $A$ containing a copy of $P$, one can delete this copy by modifying one of its locations without creating new $P$-copies in $A$. Our results address an open question of Fischer and Newman, who asked whether there exist efficient testers for properties related to tight substructures in multi-dimensional structured data. They serve as a first step towards a general understanding of local properties of multi-dimensional arrays, as any such property can be characterized by a fixed family of forbidden patterns.