Fundamental Limitations on Subquadratic Alternatives to Transformers

The Transformer architecture is widely deployed in many popular and impactful Large Language Models. At its core is the attention mechanism for calculating correlations between pairs of tokens. Performing an attention computation takes quadratic time in the input size, and had become the time bottleneck for transformer operations. In order to circumvent this, researchers have used a variety of approaches, including designing heuristic algorithms for performing attention computations faster, and proposing alternatives to the attention mechanism which can be computed more quickly. For instance, state space models such as Mamba were designed to replace attention with an almost linear time alternative. In this paper, we prove that any such approach cannot perform important tasks that Transformer is able to perform (assuming a popular conjecture from fine-grained complexity theory). We focus on document similarity tasks, where one is given as input many documents and would like to find a pair which is (approximately) the most similar. We prove that Transformer is able to perform this task, and we prove that this task cannot be performed in truly subquadratic time by any algorithm. Thus, any model which can be evaluated in subquadratic time - whether because of subquadratic-time heuristics for attention, faster attention replacements like Mamba, or any other reason - cannot perform this task. In other words, in order to perform tasks that (implicitly or explicitly) involve document similarity, one may as well use Transformer and cannot avoid its quadratic running time.

Robust Empirical Risk Minimization with Tolerance

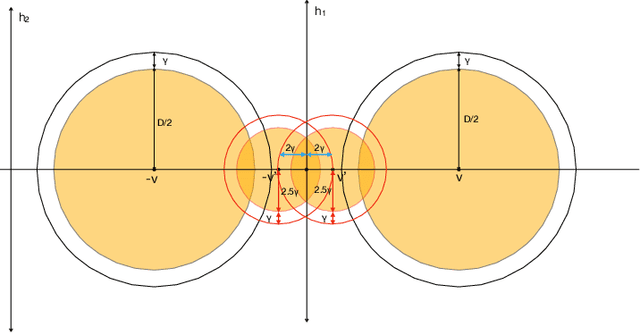
Developing simple, sample-efficient learning algorithms for robust classification is a pressing issue in today's tech-dominated world, and current theoretical techniques requiring exponential sample complexity and complicated improper learning rules fall far from answering the need. In this work we study the fundamental paradigm of (robust) $\textit{empirical risk minimization}$ (RERM), a simple process in which the learner outputs any hypothesis minimizing its training error. RERM famously fails to robustly learn VC classes (Montasser et al., 2019a), a bound we show extends even to `nice' settings such as (bounded) halfspaces. As such, we study a recent relaxation of the robust model called $\textit{tolerant}$ robust learning (Ashtiani et al., 2022) where the output classifier is compared to the best achievable error over slightly larger perturbation sets. We show that under geometric niceness conditions, a natural tolerant variant of RERM is indeed sufficient for $\gamma$-tolerant robust learning VC classes over $\mathbb{R}^d$, and requires only $\tilde{O}\left( \frac{VC(H)d\log \frac{D}{\gamma\delta}}{\epsilon^2}\right)$ samples for robustness regions of (maximum) diameter $D$.

Active Learning Polynomial Threshold Functions

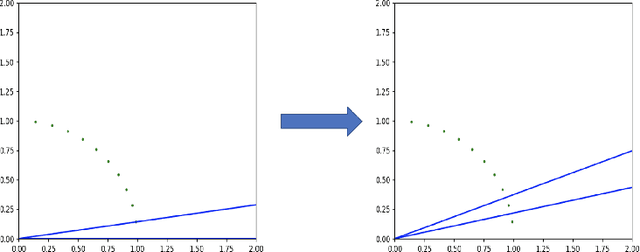
We initiate the study of active learning polynomial threshold functions (PTFs). While traditional lower bounds imply that even univariate quadratics cannot be non-trivially actively learned, we show that allowing the learner basic access to the derivatives of the underlying classifier circumvents this issue and leads to a computationally efficient algorithm for active learning degree-$d$ univariate PTFs in $\tilde{O}(d^3\log(1/\varepsilon\delta))$ queries. We also provide near-optimal algorithms and analyses for active learning PTFs in several average case settings. Finally, we prove that access to derivatives is insufficient for active learning multivariate PTFs, even those of just two variables.