From Generative to Episodic: Sample-Efficient Replicable Reinforcement Learning

The epidemic failure of replicability across empirical science and machine learning has recently motivated the formal study of replicable learning algorithms [Impagliazzo et al. (2022)]. In batch settings where data comes from a fixed i.i.d. source (e.g., hypothesis testing, supervised learning), the design of data-efficient replicable algorithms is now more or less understood. In contrast, there remain significant gaps in our knowledge for control settings like reinforcement learning where an agent must interact directly with a shifting environment. Karbasi et. al show that with access to a generative model of an environment with $S$ states and $A$ actions (the RL 'batch setting'), replicably learning a near-optimal policy costs only $\tilde{O}(S^2A^2)$ samples. On the other hand, the best upper bound without a generative model jumps to $\tilde{O}(S^7 A^7)$ [Eaton et al. (2024)] due to the substantial difficulty of environment exploration. This gap raises a key question in the broader theory of replicability: Is replicable exploration inherently more expensive than batch learning? Is sample-efficient replicable RL even possible? In this work, we (nearly) resolve this problem (for low-horizon tabular MDPs): exploration is not a significant barrier to replicable learning! Our main result is a replicable RL algorithm on $\tilde{O}(S^2A)$ samples, bridging the gap between the generative and episodic settings. We complement this with a matching $\tilde{\Omega}(S^2A)$ lower bound in the generative setting (under the common parallel sampling assumption) and an unconditional lower bound in the episodic setting of $\tilde{\Omega}(S^2)$ showcasing the near-optimality of our algorithm with respect to the state space $S$.

The Role of Randomness in Stability

Stability is a central property in learning and statistics promising the output of an algorithm $A$ does not change substantially when applied to similar datasets $S$ and $S'$. It is an elementary fact that any sufficiently stable algorithm (e.g.\ one returning the same result with high probability, satisfying privacy guarantees, etc.) must be randomized. This raises a natural question: can we quantify how much randomness is needed for algorithmic stability? We study the randomness complexity of two influential notions of stability in learning: replicability, which promises $A$ usually outputs the same result when run over samples from the same distribution (and shared random coins), and differential privacy, which promises the output distribution of $A$ remains similar under neighboring datasets. The randomness complexity of these notions was studied recently in (Dixon et al. ICML 2024) and (Cannone et al. ITCS 2024) for basic $d$-dimensional tasks (e.g. estimating the bias of $d$ coins), but little is known about the measures more generally or in complex settings like classification. Toward this end, we prove a `weak-to-strong' boosting theorem for stability: the randomness complexity of a task $M$ (either under replicability or DP) is tightly controlled by the best replication probability of any deterministic algorithm solving the task, a weak measure called `global stability' that is universally capped at $\frac{1}{2}$ (Chase et al. FOCS 2023). Using this, we characterize the randomness complexity of PAC Learning: a class has bounded randomness complexity iff it has finite Littlestone dimension, and moreover scales at worst logarithmically in the excess error of the learner. This resolves a question of (Chase et al. STOC 2024) who asked for such a characterization in the equivalent language of (error-dependent) `list-replicability'.

Replicability in High Dimensional Statistics

The replicability crisis is a major issue across nearly all areas of empirical science, calling for the formal study of replicability in statistics. Motivated in this context, [Impagliazzo, Lei, Pitassi, and Sorrell STOC 2022] introduced the notion of replicable learning algorithms, and gave basic procedures for $1$-dimensional tasks including statistical queries. In this work, we study the computational and statistical cost of replicability for several fundamental high dimensional statistical tasks, including multi-hypothesis testing and mean estimation. Our main contribution establishes a computational and statistical equivalence between optimal replicable algorithms and high dimensional isoperimetric tilings. As a consequence, we obtain matching sample complexity upper and lower bounds for replicable mean estimation of distributions with bounded covariance, resolving an open problem of [Bun, Gaboardi, Hopkins, Impagliazzo, Lei, Pitassi, Sivakumar, and Sorrell, STOC2023] and for the $N$-Coin Problem, resolving a problem of [Karbasi, Velegkas, Yang, and Zhou, NeurIPS2023] up to log factors. While our equivalence is computational, allowing us to shave log factors in sample complexity from the best known efficient algorithms, efficient isoperimetric tilings are not known. To circumvent this, we introduce several relaxed paradigms that do allow for sample and computationally efficient algorithms, including allowing pre-processing, adaptivity, and approximate replicability. In these cases we give efficient algorithms matching or beating the best known sample complexity for mean estimation and the coin problem, including a generic procedure that reduces the standard quadratic overhead of replicability to linear in expectation.

Stability is Stable: Connections between Replicability, Privacy, and Adaptive Generalization

The notion of replicable algorithms was introduced in Impagliazzo et al. [STOC '22] to describe randomized algorithms that are stable under the resampling of their inputs. More precisely, a replicable algorithm gives the same output with high probability when its randomness is fixed and it is run on a new i.i.d. sample drawn from the same distribution. Using replicable algorithms for data analysis can facilitate the verification of published results by ensuring that the results of an analysis will be the same with high probability, even when that analysis is performed on a new data set. In this work, we establish new connections and separations between replicability and standard notions of algorithmic stability. In particular, we give sample-efficient algorithmic reductions between perfect generalization, approximate differential privacy, and replicability for a broad class of statistical problems. Conversely, we show any such equivalence must break down computationally: there exist statistical problems that are easy under differential privacy, but that cannot be solved replicably without breaking public-key cryptography. Furthermore, these results are tight: our reductions are statistically optimal, and we show that any computational separation between DP and replicability must imply the existence of one-way functions. Our statistical reductions give a new algorithmic framework for translating between notions of stability, which we instantiate to answer several open questions in replicability and privacy. This includes giving sample-efficient replicable algorithms for various PAC learning, distribution estimation, and distribution testing problems, algorithmic amplification of $\delta$ in approximate DP, conversions from item-level to user-level privacy, and the existence of private agnostic-to-realizable learning reductions under structured distributions.

Do PAC-Learners Learn the Marginal Distribution?

We study a foundational variant of Valiant and Vapnik and Chervonenkis' Probably Approximately Correct (PAC)-Learning in which the adversary is restricted to a known family of marginal distributions $\mathscr{P}$. In particular, we study how the PAC-learnability of a triple $(\mathscr{P},X,H)$ relates to the learners ability to infer \emph{distributional} information about the adversary's choice of $D \in \mathscr{P}$. To this end, we introduce the `unsupervised' notion of \emph{TV-Learning}, which, given a class $(\mathscr{P},X,H)$, asks the learner to approximate $D$ from unlabeled samples with respect to a natural class-conditional total variation metric. In the classical distribution-free setting, we show that TV-learning is \emph{equivalent} to PAC-Learning: in other words, any learner must infer near-maximal information about $D$. On the other hand, we show this characterization breaks down for general $\mathscr{P}$, where PAC-Learning is strictly sandwiched between two approximate variants we call `Strong' and `Weak' TV-learning, roughly corresponding to unsupervised learners that estimate most relevant distances in $D$ with respect to $H$, but differ in whether the learner \emph{knows} the set of well-estimated events. Finally, we observe that TV-learning is in fact equivalent to the classical notion of \emph{uniform estimation}, and thereby give a strong refutation of the uniform convergence paradigm in supervised learning.

Robust Empirical Risk Minimization with Tolerance

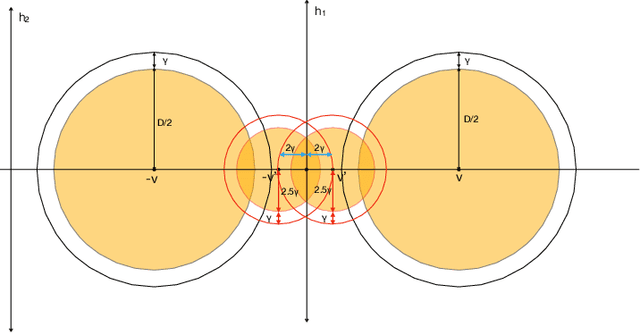
Developing simple, sample-efficient learning algorithms for robust classification is a pressing issue in today's tech-dominated world, and current theoretical techniques requiring exponential sample complexity and complicated improper learning rules fall far from answering the need. In this work we study the fundamental paradigm of (robust) $\textit{empirical risk minimization}$ (RERM), a simple process in which the learner outputs any hypothesis minimizing its training error. RERM famously fails to robustly learn VC classes (Montasser et al., 2019a), a bound we show extends even to `nice' settings such as (bounded) halfspaces. As such, we study a recent relaxation of the robust model called $\textit{tolerant}$ robust learning (Ashtiani et al., 2022) where the output classifier is compared to the best achievable error over slightly larger perturbation sets. We show that under geometric niceness conditions, a natural tolerant variant of RERM is indeed sufficient for $\gamma$-tolerant robust learning VC classes over $\mathbb{R}^d$, and requires only $\tilde{O}\left( \frac{VC(H)d\log \frac{D}{\gamma\delta}}{\epsilon^2}\right)$ samples for robustness regions of (maximum) diameter $D$.

Active Learning Polynomial Threshold Functions

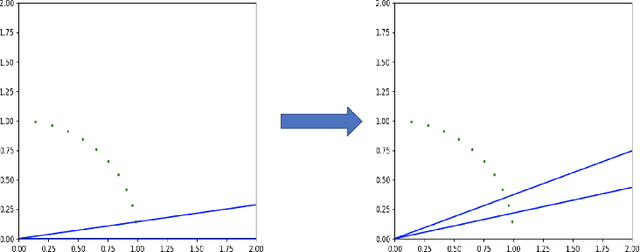
We initiate the study of active learning polynomial threshold functions (PTFs). While traditional lower bounds imply that even univariate quadratics cannot be non-trivially actively learned, we show that allowing the learner basic access to the derivatives of the underlying classifier circumvents this issue and leads to a computationally efficient algorithm for active learning degree-$d$ univariate PTFs in $\tilde{O}(d^3\log(1/\varepsilon\delta))$ queries. We also provide near-optimal algorithms and analyses for active learning PTFs in several average case settings. Finally, we prove that access to derivatives is insufficient for active learning multivariate PTFs, even those of just two variables.

Realizable Learning is All You Need

The equivalence of realizable and agnostic learnability is a fundamental phenomenon in learning theory. With variants ranging from classical settings like PAC learning and regression to recent trends such as adversarially robust and private learning, it's surprising that we still lack a unified theory; traditional proofs of the equivalence tend to be disparate, and rely on strong model-specific assumptions like uniform convergence and sample compression. In this work, we give the first model-independent framework explaining the equivalence of realizable and agnostic learnability: a three-line blackbox reduction that simplifies, unifies, and extends our understanding across a wide variety of settings. This includes models with no known characterization of learnability such as learning with arbitrary distributional assumptions or general loss, as well as a host of other popular settings such as robust learning, partial learning, fair learning, and the statistical query model. More generally, we argue that the equivalence of realizable and agnostic learning is actually a special case of a broader phenomenon we call property generalization: any desirable property of a learning algorithm (e.g.\ noise tolerance, privacy, stability) that can be satisfied over finite hypothesis classes extends (possibly in some variation) to any learnable hypothesis class.

Bounded Memory Active Learning through Enriched Queries

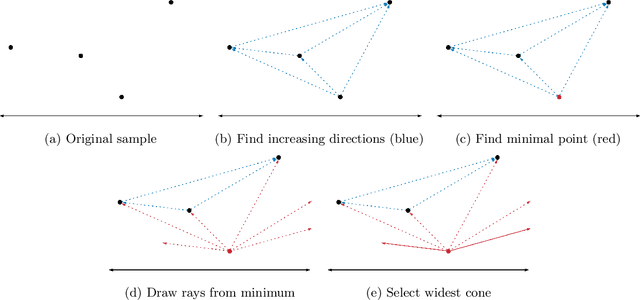
The explosive growth of easily-accessible unlabeled data has lead to growing interest in active learning, a paradigm in which data-hungry learning algorithms adaptively select informative examples in order to lower prohibitively expensive labeling costs. Unfortunately, in standard worst-case models of learning, the active setting often provides no improvement over non-adaptive algorithms. To combat this, a series of recent works have considered a model in which the learner may ask enriched queries beyond labels. While such models have seen success in drastically lowering label costs, they tend to come at the expense of requiring large amounts of memory. In this work, we study what families of classifiers can be learned in bounded memory. To this end, we introduce a novel streaming-variant of enriched-query active learning along with a natural combinatorial parameter called lossless sample compression that is sufficient for learning not only with bounded memory, but in a query-optimal and computationally efficient manner as well. Finally, we give three fundamental examples of classifier families with small, easy to compute lossless compression schemes when given access to basic enriched queries: axis-aligned rectangles, decision trees, and halfspaces in two dimensions.

Point Location and Active Learning: Learning Halfspaces Almost Optimally

Given a finite set $X \subset \mathbb{R}^d$ and a binary linear classifier $c: \mathbb{R}^d \to \{0,1\}$, how many queries of the form $c(x)$ are required to learn the label of every point in $X$? Known as \textit{point location}, this problem has inspired over 35 years of research in the pursuit of an optimal algorithm. Building on the prior work of Kane, Lovett, and Moran (ICALP 2018), we provide the first nearly optimal solution, a randomized linear decision tree of depth $\tilde{O}(d\log(|X|))$, improving on the previous best of $\tilde{O}(d^2\log(|X|))$ from Ezra and Sharir (Discrete and Computational Geometry, 2019). As a corollary, we also provide the first nearly optimal algorithm for actively learning halfspaces in the membership query model. En route to these results, we prove a novel characterization of Barthe's Theorem (Inventiones Mathematicae, 1998) of independent interest. In particular, we show that $X$ may be transformed into approximate isotropic position if and only if there exists no $k$-dimensional subspace with more than a $k/d$-fraction of $X$, and provide a similar characterization for exact isotropic position.