Poly-attention: a general scheme for higher-order self-attention

The self-attention mechanism, at the heart of the Transformer model, is able to effectively model pairwise interactions between tokens. However, numerous recent works have shown that it is unable to perform basic tasks involving detecting triples of correlated tokens, or compositional tasks where multiple input tokens need to be referenced to generate a result. Some higher-dimensional alternatives to self-attention have been proposed to address this, including higher-order attention and Strassen attention, which can perform some of these polyadic tasks in exchange for slower, superquadratic running times. In this work, we define a vast class of generalizations of self-attention, which we call poly-attention mechanisms. Our mechanisms can incorporate arbitrary higher-order (tensor) computations as well as arbitrary relationship structures between the input tokens, and they include the aforementioned alternatives as special cases. We then systematically study their computational complexity and representational strength, including giving new algorithms and matching complexity-theoretic lower bounds on the time complexity of computing the attention matrix exactly as well as approximately, and tightly determining which polyadic tasks they can each perform. Our results give interesting trade-offs between different desiderata for these mechanisms, including a tight relationship between how expressive a mechanism is, and how large the coefficients in the model may be so that the mechanism can be approximated in almost-linear time. Notably, we give a new attention mechanism which can be computed exactly in quadratic time, and which can perform function composition for any fixed number of functions. Prior mechanisms, even for just composing two functions, could only be computed in superquadratic time, and our new lower bounds show that faster algorithms for them are not possible.

Every Bit Counts: A Theoretical Study of Precision-Expressivity Tradeoffs in Quantized Transformers

Quantization reduces the numerical precision of Transformer computations and is widely used to accelerate inference, yet its effect on expressivity remains poorly characterized. We demonstrate a fine-grained theoretical tradeoff between expressivity and precision: For every p we exhibit a function Γ, inspired by the equality function, and prove that a one-layer softmax Transformer can compute Γ, with p bits of precision, but not with p-1 bits of precision. This result concretely explains the widely observed phenomenon of empirical loss of expressivity when quantization is used. Practically, it suggests that tasks requiring equality-like comparisons (exact match, membership, etc.) are especially sensitive to quantization. Dropping even one bit can cross a threshold where the model cannot represent the needed comparison reliably. Thus, it paves the way for developing heuristics that will help practitioners choose how much quantization is possible: the precision should be chosen as a function of the length of equality to be checked for the specific task. Our proofs combine explicit finite-precision Transformer constructions with communication-complexity lower bounds, yielding a tight "one-bit" threshold.

Replay Can Provably Increase Forgetting

Continual learning seeks to enable machine learning systems to solve an increasing corpus of tasks sequentially. A critical challenge for continual learning is forgetting, where the performance on previously learned tasks decreases as new tasks are introduced. One of the commonly used techniques to mitigate forgetting, sample replay, has been shown empirically to reduce forgetting by retaining some examples from old tasks and including them in new training episodes. In this work, we provide a theoretical analysis of sample replay in an over-parameterized continual linear regression setting, where each task is given by a linear subspace and with enough replay samples, one would be able to eliminate forgetting. Our analysis focuses on sample replay and highlights the role of the replayed samples and the relationship between task subspaces. Surprisingly, we find that, even in a noiseless setting, forgetting can be non-monotonic with respect to the number of replay samples. We present tasks where replay can be harmful with respect to worst-case settings, and also in distributional settings where replay of randomly selected samples increases forgetting in expectation. We also give empirical evidence that harmful replay is not limited to training with linear models by showing similar behavior for a neural networks equipped with SGD. Through experiments on a commonly used benchmark, we provide additional evidence that, even in seemingly benign scenarios, performance of the replay heavily depends on the choice of replay samples and the relationship between tasks.

Improving Predictor Reliability with Selective Recalibration

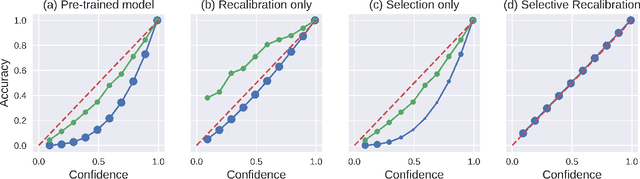
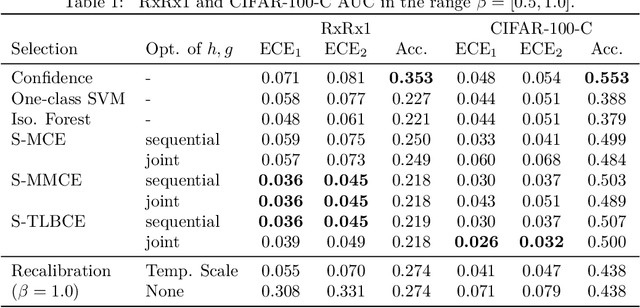
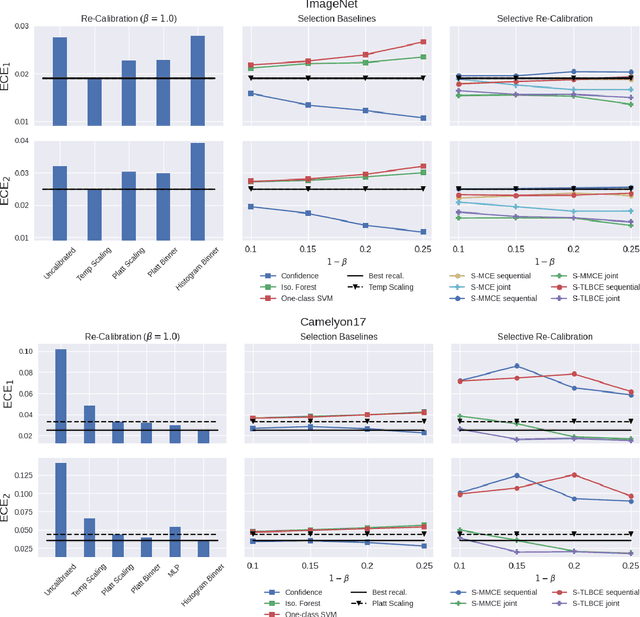
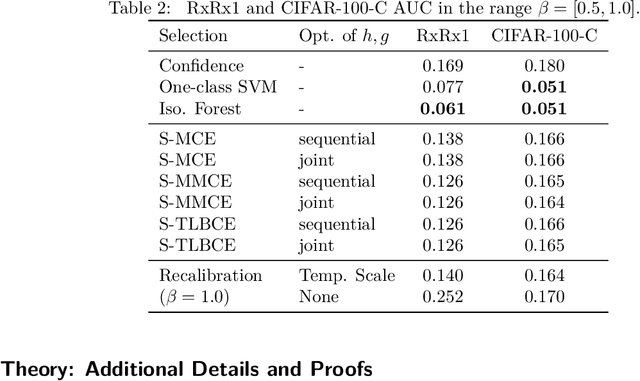
A reliable deep learning system should be able to accurately express its confidence with respect to its predictions, a quality known as calibration. One of the most effective ways to produce reliable confidence estimates with a pre-trained model is by applying a post-hoc recalibration method. Popular recalibration methods like temperature scaling are typically fit on a small amount of data and work in the model's output space, as opposed to the more expressive feature embedding space, and thus usually have only one or a handful of parameters. However, the target distribution to which they are applied is often complex and difficult to fit well with such a function. To this end we propose \textit{selective recalibration}, where a selection model learns to reject some user-chosen proportion of the data in order to allow the recalibrator to focus on regions of the input space that can be well-captured by such a model. We provide theoretical analysis to motivate our algorithm, and test our method through comprehensive experiments on difficult medical imaging and zero-shot classification tasks. Our results show that selective recalibration consistently leads to significantly lower calibration error than a wide range of selection and recalibration baselines.

Prompt Risk Control: A Rigorous Framework for Responsible Deployment of Large Language Models

The recent explosion in the capabilities of large language models has led to a wave of interest in how best to prompt a model to perform a given task. While it may be tempting to simply choose a prompt based on average performance on a validation set, this can lead to a deployment where unexpectedly poor responses are generated, especially for the worst-off users. To mitigate this prospect, we propose Prompt Risk Control, a lightweight framework for selecting a prompt based on rigorous upper bounds on families of informative risk measures. We offer methods for producing bounds on a diverse set of metrics, including quantities that measure worst-case responses and disparities in generation quality across the population of users. In addition, we extend the underlying statistical bounding techniques to accommodate the possibility of distribution shifts in deployment. Experiments on applications such as open-ended chat, medical question summarization, and code generation highlight how such a framework can foster responsible deployment by reducing the risk of the worst outcomes.

Distribution-Free Statistical Dispersion Control for Societal Applications

Explicit finite-sample statistical guarantees on model performance are an important ingredient in responsible machine learning. Previous work has focused mainly on bounding either the expected loss of a predictor or the probability that an individual prediction will incur a loss value in a specified range. However, for many high-stakes applications, it is crucial to understand and control the dispersion of a loss distribution, or the extent to which different members of a population experience unequal effects of algorithmic decisions. We initiate the study of distribution-free control of statistical dispersion measures with societal implications and propose a simple yet flexible framework that allows us to handle a much richer class of statistical functionals beyond previous work. Our methods are verified through experiments in toxic comment detection, medical imaging, and film recommendation.

Stability is Stable: Connections between Replicability, Privacy, and Adaptive Generalization

The notion of replicable algorithms was introduced in Impagliazzo et al. [STOC '22] to describe randomized algorithms that are stable under the resampling of their inputs. More precisely, a replicable algorithm gives the same output with high probability when its randomness is fixed and it is run on a new i.i.d. sample drawn from the same distribution. Using replicable algorithms for data analysis can facilitate the verification of published results by ensuring that the results of an analysis will be the same with high probability, even when that analysis is performed on a new data set. In this work, we establish new connections and separations between replicability and standard notions of algorithmic stability. In particular, we give sample-efficient algorithmic reductions between perfect generalization, approximate differential privacy, and replicability for a broad class of statistical problems. Conversely, we show any such equivalence must break down computationally: there exist statistical problems that are easy under differential privacy, but that cannot be solved replicably without breaking public-key cryptography. Furthermore, these results are tight: our reductions are statistically optimal, and we show that any computational separation between DP and replicability must imply the existence of one-way functions. Our statistical reductions give a new algorithmic framework for translating between notions of stability, which we instantiate to answer several open questions in replicability and privacy. This includes giving sample-efficient replicable algorithms for various PAC learning, distribution estimation, and distribution testing problems, algorithmic amplification of $\delta$ in approximate DP, conversions from item-level to user-level privacy, and the existence of private agnostic-to-realizable learning reductions under structured distributions.

Quantile Risk Control: A Flexible Framework for Bounding the Probability of High-Loss Predictions

Rigorous guarantees about the performance of predictive algorithms are necessary in order to ensure their responsible use. Previous work has largely focused on bounding the expected loss of a predictor, but this is not sufficient in many risk-sensitive applications where the distribution of errors is important. In this work, we propose a flexible framework to produce a family of bounds on quantiles of the loss distribution incurred by a predictor. Our method takes advantage of the order statistics of the observed loss values rather than relying on the sample mean alone. We show that a quantile is an informative way of quantifying predictive performance, and that our framework applies to a variety of quantile-based metrics, each targeting important subsets of the data distribution. We analyze the theoretical properties of our proposed method and demonstrate its ability to rigorously control loss quantiles on several real-world datasets.

Learning versus Refutation in Noninteractive Local Differential Privacy

We study two basic statistical tasks in non-interactive local differential privacy (LDP): learning and refutation. Learning requires finding a concept that best fits an unknown target function (from labelled samples drawn from a distribution), whereas refutation requires distinguishing between data distributions that are well-correlated with some concept in the class, versus distributions where the labels are random. Our main result is a complete characterization of the sample complexity of agnostic PAC learning for non-interactive LDP protocols. We show that the optimal sample complexity for any concept class is captured by the approximate $\gamma_2$~norm of a natural matrix associated with the class. Combined with previous work [Edmonds, Nikolov and Ullman, 2019] this gives an equivalence between learning and refutation in the agnostic setting.

Reproducibility in Learning

We introduce the notion of a reproducible algorithm in the context of learning. A reproducible learning algorithm is resilient to variations in its samples -- with high probability, it returns the exact same output when run on two samples from the same underlying distribution. We begin by unpacking the definition, clarifying how randomness is instrumental in balancing accuracy and reproducibility. We initiate a theory of reproducible algorithms, showing how reproducibility implies desirable properties such as data reuse and efficient testability. Despite the exceedingly strong demand of reproducibility, there are efficient reproducible algorithms for several fundamental problems in statistics and learning. First, we show that any statistical query algorithm can be made reproducible with a modest increase in sample complexity, and we use this to construct reproducible algorithms for finding approximate heavy-hitters and medians. Using these ideas, we give the first reproducible algorithm for learning halfspaces via a reproducible weak learner and a reproducible boosting algorithm. Finally, we initiate the study of lower bounds and inherent tradeoffs for reproducible algorithms, giving nearly tight sample complexity upper and lower bounds for reproducible versus nonreproducible SQ algorithms.