Replicable Reinforcement Learning with Linear Function Approximation

Replication of experimental results has been a challenge faced by many scientific disciplines, including the field of machine learning. Recent work on the theory of machine learning has formalized replicability as the demand that an algorithm produce identical outcomes when executed twice on different samples from the same distribution. Provably replicable algorithms are especially interesting for reinforcement learning (RL), where algorithms are known to be unstable in practice. While replicable algorithms exist for tabular RL settings, extending these guarantees to more practical function approximation settings has remained an open problem. In this work, we make progress by developing replicable methods for linear function approximation in RL. We first introduce two efficient algorithms for replicable random design regression and uncentered covariance estimation, each of independent interest. We then leverage these tools to provide the first provably efficient replicable RL algorithms for linear Markov decision processes in both the generative model and episodic settings. Finally, we evaluate our algorithms experimentally and show how they can inspire more consistent neural policies.

Sensitivity of Stability: Theoretical & Empirical Analysis of Replicability for Adaptive Data Selection in Transfer Learning

The widespread adoption of transfer learning has revolutionized machine learning by enabling efficient adaptation of pre-trained models to new domains. However, the reliability of these adaptations remains poorly understood, particularly when using adaptive data selection strategies that dynamically prioritize training examples. We present a comprehensive theoretical and empirical analysis of replicability in transfer learning, introducing a mathematical framework that quantifies the fundamental trade-off between adaptation effectiveness and result consistency. Our key contribution is the formalization of selection sensitivity ($\Delta_Q$), a measure that captures how adaptive selection strategies respond to perturbations in training data. We prove that replicability failure probability: the likelihood that two independent training runs produce models differing in performance by more than a threshold, increases quadratically with selection sensitivity while decreasing exponentially with sample size. Through extensive experiments on the MultiNLI corpus using six adaptive selection strategies - ranging from uniform sampling to gradient-based selection - we demonstrate that this theoretical relationship holds precisely in practice. Our results reveal that highly adaptive strategies like gradient-based and curriculum learning achieve superior task performance but suffer from high replicability failure rates, while less adaptive approaches maintain failure rates below 7%. Crucially, we show that source domain pretraining provides a powerful mitigation mechanism, reducing failure rates by up to 30% while preserving performance gains. These findings establish principled guidelines for practitioners to navigate the performance-replicability trade-off and highlight the need for replicability-aware design in modern transfer learning systems.

Intersectional Fairness in Reinforcement Learning with Large State and Constraint Spaces

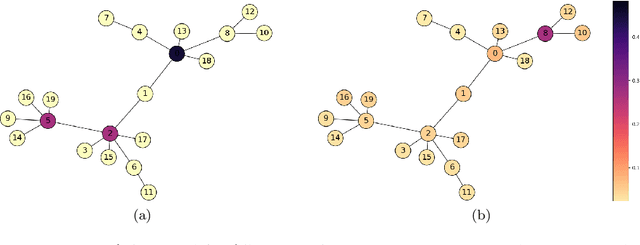
In traditional reinforcement learning (RL), the learner aims to solve a single objective optimization problem: find the policy that maximizes expected reward. However, in many real-world settings, it is important to optimize over multiple objectives simultaneously. For example, when we are interested in fairness, states might have feature annotations corresponding to multiple (intersecting) demographic groups to whom reward accrues, and our goal might be to maximize the reward of the group receiving the minimal reward. In this work, we consider a multi-objective optimization problem in which each objective is defined by a state-based reweighting of a single scalar reward function. This generalizes the problem of maximizing the reward of the minimum reward group. We provide oracle-efficient algorithms to solve these multi-objective RL problems even when the number of objectives is exponentially large-for tabular MDPs, as well as for large MDPs when the group functions have additional structure. Finally, we experimentally validate our theoretical results and demonstrate applications on a preferential attachment graph MDP.

The Cost of Replicability in Active Learning

Active learning aims to reduce the required number of labeled data for machine learning algorithms by selectively querying the labels of initially unlabeled data points. Ensuring the replicability of results, where an algorithm consistently produces the same outcome across different runs, is essential for the reliability of machine learning models but often increases sample complexity. This report investigates the cost of replicability in active learning using the CAL algorithm, a classical disagreement-based active learning method. By integrating replicable statistical query subroutines and random thresholding techniques, we propose two versions of a replicable CAL algorithm. Our theoretical analysis demonstrates that while replicability does increase label complexity, the CAL algorithm can still achieve significant savings in label complexity even with the replicability constraint. These findings offer valuable insights into balancing efficiency and robustness in machine learning models.

Oracle-Efficient Reinforcement Learning for Max Value Ensembles

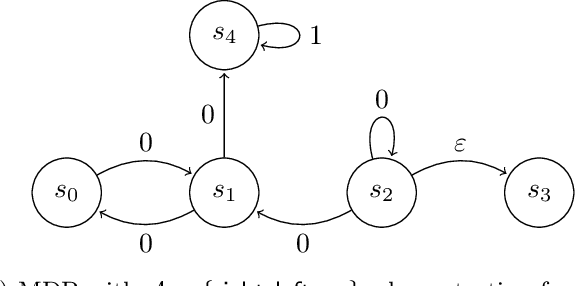
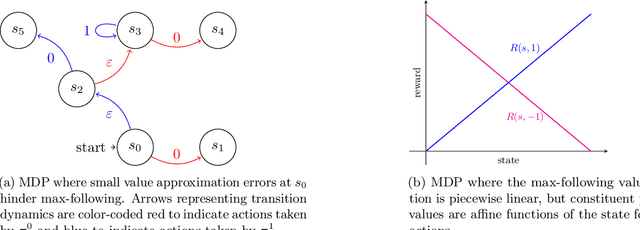
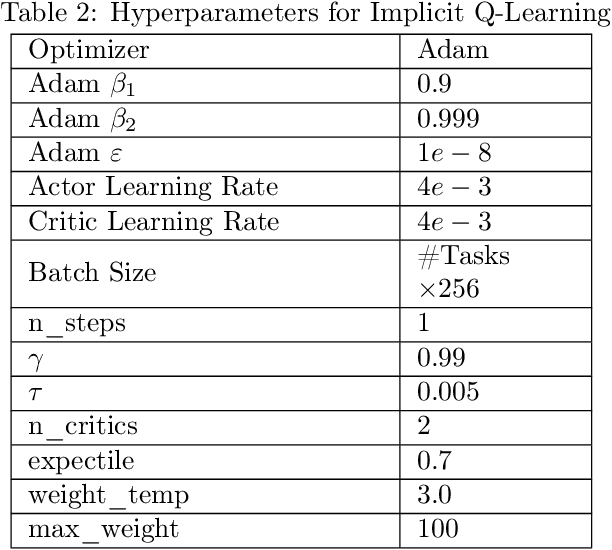
Reinforcement learning (RL) in large or infinite state spaces is notoriously challenging, both theoretically (where worst-case sample and computational complexities must scale with state space cardinality) and experimentally (where function approximation and policy gradient techniques often scale poorly and suffer from instability and high variance). One line of research attempting to address these difficulties makes the natural assumption that we are given a collection of heuristic base or $\textit{constituent}$ policies upon which we would like to improve in a scalable manner. In this work we aim to compete with the $\textit{max-following policy}$, which at each state follows the action of whichever constituent policy has the highest value. The max-following policy is always at least as good as the best constituent policy, and may be considerably better. Our main result is an efficient algorithm that learns to compete with the max-following policy, given only access to the constituent policies (but not their value functions). In contrast to prior work in similar settings, our theoretical results require only the minimal assumption of an ERM oracle for value function approximation for the constituent policies (and not the global optimal policy or the max-following policy itself) on samplable distributions. We illustrate our algorithm's experimental effectiveness and behavior on several robotic simulation testbeds.

Replicable Reinforcement Learning

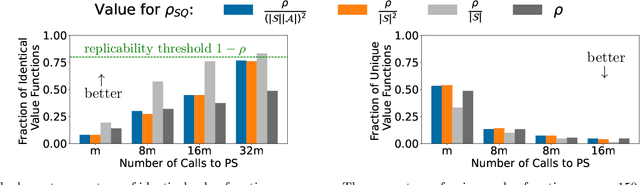
The replicability crisis in the social, behavioral, and data sciences has led to the formulation of algorithm frameworks for replicability -- i.e., a requirement that an algorithm produce identical outputs (with high probability) when run on two different samples from the same underlying distribution. While still in its infancy, provably replicable algorithms have been developed for many fundamental tasks in machine learning and statistics, including statistical query learning, the heavy hitters problem, and distribution testing. In this work we initiate the study of replicable reinforcement learning, providing a provably replicable algorithm for parallel value iteration, and a provably replicable version of R-max in the episodic setting. These are the first formal replicability results for control problems, which present different challenges for replication than batch learning settings.

Stability is Stable: Connections between Replicability, Privacy, and Adaptive Generalization

The notion of replicable algorithms was introduced in Impagliazzo et al. [STOC '22] to describe randomized algorithms that are stable under the resampling of their inputs. More precisely, a replicable algorithm gives the same output with high probability when its randomness is fixed and it is run on a new i.i.d. sample drawn from the same distribution. Using replicable algorithms for data analysis can facilitate the verification of published results by ensuring that the results of an analysis will be the same with high probability, even when that analysis is performed on a new data set. In this work, we establish new connections and separations between replicability and standard notions of algorithmic stability. In particular, we give sample-efficient algorithmic reductions between perfect generalization, approximate differential privacy, and replicability for a broad class of statistical problems. Conversely, we show any such equivalence must break down computationally: there exist statistical problems that are easy under differential privacy, but that cannot be solved replicably without breaking public-key cryptography. Furthermore, these results are tight: our reductions are statistically optimal, and we show that any computational separation between DP and replicability must imply the existence of one-way functions. Our statistical reductions give a new algorithmic framework for translating between notions of stability, which we instantiate to answer several open questions in replicability and privacy. This includes giving sample-efficient replicable algorithms for various PAC learning, distribution estimation, and distribution testing problems, algorithmic amplification of $\delta$ in approximate DP, conversions from item-level to user-level privacy, and the existence of private agnostic-to-realizable learning reductions under structured distributions.

Multicalibration as Boosting for Regression

We study the connection between multicalibration and boosting for squared error regression. First we prove a useful characterization of multicalibration in terms of a ``swap regret'' like condition on squared error. Using this characterization, we give an exceedingly simple algorithm that can be analyzed both as a boosting algorithm for regression and as a multicalibration algorithm for a class H that makes use only of a standard squared error regression oracle for H. We give a weak learning assumption on H that ensures convergence to Bayes optimality without the need to make any realizability assumptions -- giving us an agnostic boosting algorithm for regression. We then show that our weak learning assumption on H is both necessary and sufficient for multicalibration with respect to H to imply Bayes optimality. We also show that if H satisfies our weak learning condition relative to another class C then multicalibration with respect to H implies multicalibration with respect to C. Finally we investigate the empirical performance of our algorithm experimentally using an open source implementation that we make available. Our code repository can be found at https://github.com/Declancharrison/Level-Set-Boosting.

Reproducibility in Learning

We introduce the notion of a reproducible algorithm in the context of learning. A reproducible learning algorithm is resilient to variations in its samples -- with high probability, it returns the exact same output when run on two samples from the same underlying distribution. We begin by unpacking the definition, clarifying how randomness is instrumental in balancing accuracy and reproducibility. We initiate a theory of reproducible algorithms, showing how reproducibility implies desirable properties such as data reuse and efficient testability. Despite the exceedingly strong demand of reproducibility, there are efficient reproducible algorithms for several fundamental problems in statistics and learning. First, we show that any statistical query algorithm can be made reproducible with a modest increase in sample complexity, and we use this to construct reproducible algorithms for finding approximate heavy-hitters and medians. Using these ideas, we give the first reproducible algorithm for learning halfspaces via a reproducible weak learner and a reproducible boosting algorithm. Finally, we initiate the study of lower bounds and inherent tradeoffs for reproducible algorithms, giving nearly tight sample complexity upper and lower bounds for reproducible versus nonreproducible SQ algorithms.

Boosting in the Presence of Massart Noise

We study the problem of boosting the accuracy of a weak learner in the (distribution-independent) PAC model with Massart noise. In the Massart noise model, the label of each example $x$ is independently misclassified with probability $\eta(x) \leq \eta$, where $\eta<1/2$. The Massart model lies between the random classification noise model and the agnostic model. Our main positive result is the first computationally efficient boosting algorithm in the presence of Massart noise that achieves misclassification error arbitrarily close to $\eta$. Prior to our work, no non-trivial booster was known in this setting. Moreover, we show that this error upper bound is best possible for polynomial-time black-box boosters, under standard cryptographic assumptions. Our upper and lower bounds characterize the complexity of boosting in the distribution-independent PAC model with Massart noise. As a simple application of our positive result, we give the first efficient Massart learner for unions of high-dimensional rectangles.