Oracle-Efficient Reinforcement Learning for Max Value Ensembles
Paper and Code
May 27, 2024
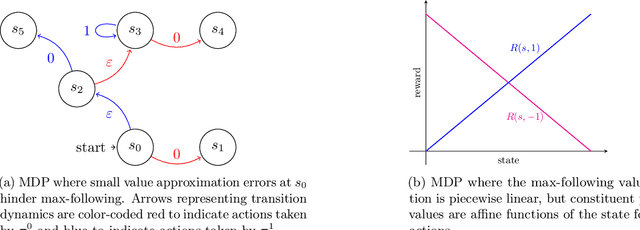
Reinforcement learning (RL) in large or infinite state spaces is notoriously challenging, both theoretically (where worst-case sample and computational complexities must scale with state space cardinality) and experimentally (where function approximation and policy gradient techniques often scale poorly and suffer from instability and high variance). One line of research attempting to address these difficulties makes the natural assumption that we are given a collection of heuristic base or $\textit{constituent}$ policies upon which we would like to improve in a scalable manner. In this work we aim to compete with the $\textit{max-following policy}$, which at each state follows the action of whichever constituent policy has the highest value. The max-following policy is always at least as good as the best constituent policy, and may be considerably better. Our main result is an efficient algorithm that learns to compete with the max-following policy, given only access to the constituent policies (but not their value functions). In contrast to prior work in similar settings, our theoretical results require only the minimal assumption of an ERM oracle for value function approximation for the constituent policies (and not the global optimal policy or the max-following policy itself) on samplable distributions. We illustrate our algorithm's experimental effectiveness and behavior on several robotic simulation testbeds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge