Two heads are better than one: simulating large transformers with small ones

The quadratic complexity of self-attention prevents transformers from scaling effectively to long input sequences. On the other hand, modern GPUs and other specialized hardware accelerators are well-optimized for processing small input sequences in transformers during both training and inference. A natural question arises: can we take advantage of the efficiency of small transformers to deal with long input sequences? In this paper, we show that transformers with long input sequences (large transformers) can be efficiently simulated by transformers that can only take short input sequences (small transformers). Specifically, we prove that any transformer with input length $N$ can be efficiently simulated by only $O((N/M)^2)$ transformers with input length $M \ll N$, and that this cannot be improved in the worst case. However, we then prove that in various natural scenarios including average-case inputs, sliding window masking and attention sinks, the optimal number $O(N/M)$ of small transformers suffice.

Only Large Weights (And Not Skip Connections) Can Prevent the Perils of Rank Collapse

Attention mechanisms lie at the heart of modern large language models (LLMs). Straightforward algorithms for forward and backward (gradient) computation take quadratic time, and a line of work initiated by [Alman and Song NeurIPS 2023] and [Alman and Song NeurIPS 2024] has shown that quadratic time is necessary unless the model weights are small, in which case almost linear time algorithms are possible. In this paper, we show that large weights are necessary to avoid a strong preclusion to representational strength we call layer collapse, which means that the entire network can be approximated well by a network with only a single layer. Thus, the quadratic running time of attention is unavoidable for expressive transformers. The notion of layer collapse that we introduce is a variant on the notion of rank collapse from the work of [Dong, Cordonnier, and Loukas ICML 2021]. They showed that in Self Attention Networks with small weights and with skip connections, rank collapse must occur. This is typically interpreted as justifying the necessity of skip connections in expressive networks. However, our result shows that even with skip connections, if the weights are small, then layer collapse still occurs. Thus, only large weights, and not skip connections, can prevent these representational weaknesses.

Fast RoPE Attention: Combining the Polynomial Method and Fast Fourier Transform

The transformer architecture has been widely applied to many machine learning tasks. A main bottleneck in the time to perform transformer computations is a task called attention computation. [Alman and Song, NeurIPS 2023] have shown that in the bounded entry regime, there is an almost linear time algorithm to approximate the attention computation. They also proved that the bounded entry assumption is necessary for a fast algorithm assuming the popular Strong Exponential Time Hypothesis. A new version of transformer which uses position embeddings has recently been very successful. At a high level, position embedding enables the model to capture the correlations between tokens while taking into account their position in the sequence. Perhaps the most popular and effective version is Rotary Position Embedding (RoPE), which was proposed by [Su, Lu, Pan, Murtadha, Wen, and Liu, Neurocomputing 2024]. A main downside of RoPE is that it complicates the attention computation problem, so that previous techniques for designing almost linear time algorithms no longer seem to work. In this paper, we show how to overcome this issue, and give a new algorithm to compute the RoPE attention in almost linear time in the bounded entry regime. (Again, known lower bounds imply that bounded entries are necessary.) Our new algorithm combines two techniques in a novel way: the polynomial method, which was used in prior fast attention algorithms, and the Fast Fourier Transform.

Fundamental Limitations on Subquadratic Alternatives to Transformers

The Transformer architecture is widely deployed in many popular and impactful Large Language Models. At its core is the attention mechanism for calculating correlations between pairs of tokens. Performing an attention computation takes quadratic time in the input size, and had become the time bottleneck for transformer operations. In order to circumvent this, researchers have used a variety of approaches, including designing heuristic algorithms for performing attention computations faster, and proposing alternatives to the attention mechanism which can be computed more quickly. For instance, state space models such as Mamba were designed to replace attention with an almost linear time alternative. In this paper, we prove that any such approach cannot perform important tasks that Transformer is able to perform (assuming a popular conjecture from fine-grained complexity theory). We focus on document similarity tasks, where one is given as input many documents and would like to find a pair which is (approximately) the most similar. We prove that Transformer is able to perform this task, and we prove that this task cannot be performed in truly subquadratic time by any algorithm. Thus, any model which can be evaluated in subquadratic time - whether because of subquadratic-time heuristics for attention, faster attention replacements like Mamba, or any other reason - cannot perform this task. In other words, in order to perform tasks that (implicitly or explicitly) involve document similarity, one may as well use Transformer and cannot avoid its quadratic running time.

The Fine-Grained Complexity of Gradient Computation for Training Large Language Models

Large language models (LLMs) have made fundamental contributions over the last a few years. To train an LLM, one needs to alternatingly run `forward' computations and `backward' computations. The forward computation can be viewed as attention function evaluation, and the backward computation can be viewed as a gradient computation. In previous work by [Alman and Song, NeurIPS 2023], it was proved that the forward step can be performed in almost-linear time in certain parameter regimes, but that there is no truly sub-quadratic time algorithm in the remaining parameter regimes unless the popular hypothesis SETH is false. In this work, we show nearly identical results for the harder-seeming problem of computing the gradient of loss function of one layer attention network, and thus for the entire process of LLM training. This completely characterizes the fine-grained complexity of every step of LLM training.

How to Capture Higher-order Correlations? Generalizing Matrix Softmax Attention to Kronecker Computation

In the classical transformer attention scheme, we are given three $n \times d$ size matrices $Q, K, V$ (the query, key, and value tokens), and the goal is to compute a new $n \times d$ size matrix $D^{-1} \exp(QK^\top) V$ where $D = \mathrm{diag}( \exp(QK^\top) {\bf 1}_n )$. In this work, we study a generalization of attention which captures triple-wise correlations. This generalization is able to solve problems about detecting triple-wise connections that were shown to be impossible for transformers. The potential downside of this generalization is that it appears as though computations are even more difficult, since the straightforward algorithm requires cubic time in $n$. However, we show that in the bounded-entry setting (which arises in practice, and which is well-studied in both theory and practice), there is actually a near-linear time algorithm. More precisely, we show that bounded entries are both necessary and sufficient for quickly performing generalized computations: $\bullet$ On the positive side, if all entries of the input matrices are bounded above by $o(\sqrt[3]{\log n})$ then we show how to approximate the ``tensor-type'' attention matrix in $n^{1+o(1)}$ time. $\bullet$ On the negative side, we show that if the entries of the input matrices may be as large as $\Omega(\sqrt[3]{\log n})$, then there is no algorithm that runs faster than $n^{3-o(1)}$ (assuming the Strong Exponential Time Hypothesis from fine-grained complexity theory). We also show that our construction, algorithms, and lower bounds naturally generalize to higher-order tensors and correlations. Interestingly, the higher the order of the tensors, the lower the bound on the entries needs to be for an efficient algorithm. Our results thus yield a natural tradeoff between the boundedness of the entries, and order of the tensor one may use for more expressive, efficient attention computation.

Fast Attention Requires Bounded Entries

In modern machine learning, inner product attention computation is a fundamental task for training large language models such as Transformer, GPT-1, BERT, GPT-2, GPT-3 and ChatGPT. Formally, in this problem, one is given as input three matrices $Q, K, V \in [-B,B]^{n \times d}$, and the goal is to construct the matrix $\mathrm{Att}(Q,K,V) := \mathrm{diag}(A {\bf 1}_n)^{-1} A V \in \mathbb{R}^{n \times d}$, where $A = \exp(QK^\top/d)$ is the `attention matrix', and $\exp$ is applied entry-wise. Straightforward methods for this problem explicitly compute the $n \times n$ attention matrix $A$, and hence require time $\Omega(n^2)$ even when $d = n^{o(1)}$ is small. In this paper, we investigate whether faster algorithms are possible by implicitly making use of the matrix $A$. We present two results, showing that there is a sharp transition at $B = \Theta(\sqrt{\log n})$. $\bullet$ If $d = O(\log n)$ and $B = o(\sqrt{\log n})$, there is an $n^{1+o(1)}$ time algorithm to approximate $\mathrm{Att}(Q,K,V)$ up to $1/\mathrm{poly}(n)$ additive error. $\bullet$ If $d = O(\log n)$ and $B = \Theta (\sqrt{\log n})$, assuming the Strong Exponential Time Hypothesis from fine-grained complexity theory, it is impossible to approximate $\mathrm{Att}(Q,K,V)$ up to $1/\mathrm{poly}(n)$ additive error in truly subquadratic time $n^{2 - \Omega(1)}$. This gives a theoretical explanation for the phenomenon observed in practice that attention computation is much more efficient when the input matrices have smaller entries.

Bypass Exponential Time Preprocessing: Fast Neural Network Training via Weight-Data Correlation Preprocessing

Over the last decade, deep neural networks have transformed our society, and they are already widely applied in various machine learning applications. State-of-art deep neural networks are becoming larger in size every year to deliver increasing model accuracy, and as a result, model training consumes substantial computing resources and will only consume more in the future. Using current training methods, in each iteration, to process a data point $x \in \mathbb{R}^d$ in a layer, we need to spend $\Theta(md)$ time to evaluate all the $m$ neurons in the layer. This means processing the entire layer takes $\Theta(nmd)$ time for $n$ data points. Recent work [Song, Yang and Zhang, NeurIPS 2021] reduces this time per iteration to $o(nmd)$, but requires exponential time to preprocess either the data or the neural network weights, making it unlikely to have practical usage. In this work, we present a new preprocessing method that simply stores the weight-data correlation in a tree data structure in order to quickly, dynamically detect which neurons fire at each iteration. Our method requires only $O(nmd)$ time in preprocessing and still achieves $o(nmd)$ time per iteration. We complement our new algorithm with a lower bound, proving that assuming a popular conjecture from complexity theory, one could not substantially speed up our algorithm for dynamic detection of firing neurons.

Algorithms and Hardness for Linear Algebra on Geometric Graphs

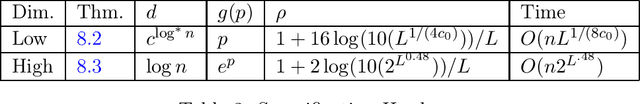
For a function $\mathsf{K} : \mathbb{R}^{d} \times \mathbb{R}^{d} \to \mathbb{R}_{\geq 0}$, and a set $P = \{ x_1, \ldots, x_n\} \subset \mathbb{R}^d$ of $n$ points, the $\mathsf{K}$ graph $G_P$ of $P$ is the complete graph on $n$ nodes where the weight between nodes $i$ and $j$ is given by $\mathsf{K}(x_i, x_j)$. In this paper, we initiate the study of when efficient spectral graph theory is possible on these graphs. We investigate whether or not it is possible to solve the following problems in $n^{1+o(1)}$ time for a $\mathsf{K}$-graph $G_P$ when $d < n^{o(1)}$: $\bullet$ Multiply a given vector by the adjacency matrix or Laplacian matrix of $G_P$ $\bullet$ Find a spectral sparsifier of $G_P$ $\bullet$ Solve a Laplacian system in $G_P$'s Laplacian matrix For each of these problems, we consider all functions of the form $\mathsf{K}(u,v) = f(\|u-v\|_2^2)$ for a function $f:\mathbb{R} \rightarrow \mathbb{R}$. We provide algorithms and comparable hardness results for many such $\mathsf{K}$, including the Gaussian kernel, Neural tangent kernels, and more. For example, in dimension $d = \Omega(\log n)$, we show that there is a parameter associated with the function $f$ for which low parameter values imply $n^{1+o(1)}$ time algorithms for all three of these problems and high parameter values imply the nonexistence of subquadratic time algorithms assuming Strong Exponential Time Hypothesis ($\mathsf{SETH}$), given natural assumptions on $f$. As part of our results, we also show that the exponential dependence on the dimension $d$ in the celebrated fast multipole method of Greengard and Rokhlin cannot be improved, assuming $\mathsf{SETH}$, for a broad class of functions $f$. To the best of our knowledge, this is the first formal limitation proven about fast multipole methods.