Self-Evolution Fine-Tuning for Policy Optimization

The alignment of large language models (LLMs) is crucial not only for unlocking their potential in specific tasks but also for ensuring that responses meet human expectations and adhere to safety and ethical principles. Current alignment methodologies face considerable challenges. For instance, supervised fine-tuning (SFT) requires extensive, high-quality annotated samples, while reinforcement learning from human feedback (RLHF) is complex and often unstable. In this paper, we introduce self-evolution fine-tuning (SEFT) for policy optimization, with the aim of eliminating the need for annotated samples while retaining the stability and efficiency of SFT. SEFT first trains an adaptive reviser to elevate low-quality responses while maintaining high-quality ones. The reviser then gradually guides the policy's optimization by fine-tuning it with enhanced responses. One of the prominent features of this method is its ability to leverage unlimited amounts of unannotated data for policy optimization through supervised fine-tuning. Our experiments on AlpacaEval 2.0 and MT-Bench demonstrate the effectiveness of SEFT. We also provide a comprehensive analysis of its advantages over existing alignment techniques.

A Faster $k$-means++ Algorithm

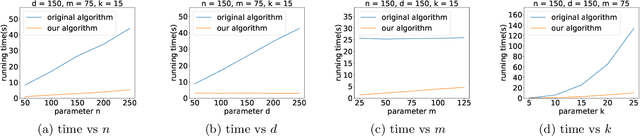
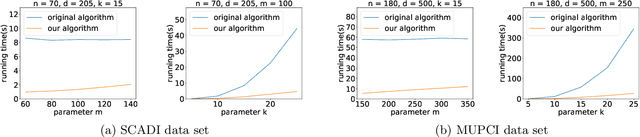
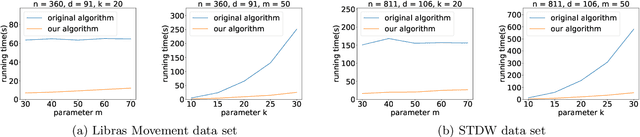
K-means++ is an important algorithm to choose initial cluster centers for the k-means clustering algorithm. In this work, we present a new algorithm that can solve the $k$-means++ problem with near optimal running time. Given $n$ data points in $\mathbb{R}^d$, the current state-of-the-art algorithm runs in $\widetilde{O}(k )$ iterations, and each iteration takes $\widetilde{O}(nd k)$ time. The overall running time is thus $\widetilde{O}(n d k^2)$. We propose a new algorithm \textsc{FastKmeans++} that only takes in $\widetilde{O}(nd + nk^2)$ time, in total.

Bypass Exponential Time Preprocessing: Fast Neural Network Training via Weight-Data Correlation Preprocessing

Over the last decade, deep neural networks have transformed our society, and they are already widely applied in various machine learning applications. State-of-art deep neural networks are becoming larger in size every year to deliver increasing model accuracy, and as a result, model training consumes substantial computing resources and will only consume more in the future. Using current training methods, in each iteration, to process a data point $x \in \mathbb{R}^d$ in a layer, we need to spend $\Theta(md)$ time to evaluate all the $m$ neurons in the layer. This means processing the entire layer takes $\Theta(nmd)$ time for $n$ data points. Recent work [Song, Yang and Zhang, NeurIPS 2021] reduces this time per iteration to $o(nmd)$, but requires exponential time to preprocess either the data or the neural network weights, making it unlikely to have practical usage. In this work, we present a new preprocessing method that simply stores the weight-data correlation in a tree data structure in order to quickly, dynamically detect which neurons fire at each iteration. Our method requires only $O(nmd)$ time in preprocessing and still achieves $o(nmd)$ time per iteration. We complement our new algorithm with a lower bound, proving that assuming a popular conjecture from complexity theory, one could not substantially speed up our algorithm for dynamic detection of firing neurons.

Dynamic Maintenance of Kernel Density Estimation Data Structure: From Practice to Theory

Kernel density estimation (KDE) stands out as a challenging task in machine learning. The problem is defined in the following way: given a kernel function $f(x,y)$ and a set of points $\{x_1, x_2, \cdots, x_n \} \subset \mathbb{R}^d$, we would like to compute $\frac{1}{n}\sum_{i=1}^{n} f(x_i,y)$ for any query point $y \in \mathbb{R}^d$. Recently, there has been a growing trend of using data structures for efficient KDE. However, the proposed KDE data structures focus on static settings. The robustness of KDE data structures over dynamic changing data distributions is not addressed. In this work, we focus on the dynamic maintenance of KDE data structures with robustness to adversarial queries. Especially, we provide a theoretical framework of KDE data structures. In our framework, the KDE data structures only require subquadratic spaces. Moreover, our data structure supports the dynamic update of the dataset in sublinear time. Furthermore, we can perform adaptive queries with the potential adversary in sublinear time.