Chenbo Yin
Fast and Efficient Matching Algorithm with Deadline Instances
May 15, 2023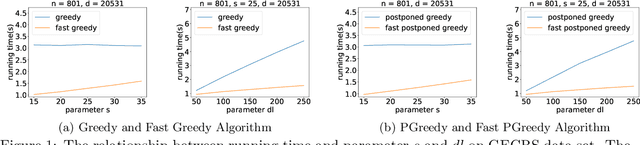

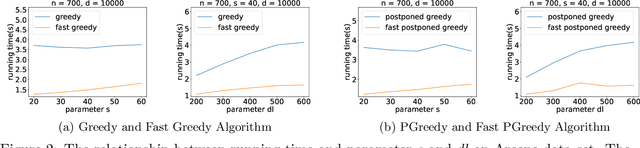

Abstract:Online weighted matching problem is a fundamental problem in machine learning due to its numerous applications. Despite many efforts in this area, existing algorithms are either too slow or don't take $\mathrm{deadline}$ (the longest time a node can be matched) into account. In this paper, we introduce a market model with $\mathrm{deadline}$ first. Next, we present our two optimized algorithms (\textsc{FastGreedy} and \textsc{FastPostponedGreedy}) and offer theoretical proof of the time complexity and correctness of our algorithms. In \textsc{FastGreedy} algorithm, we have already known if a node is a buyer or a seller. But in \textsc{FastPostponedGreedy} algorithm, the status of each node is unknown at first. Then, we generalize a sketching matrix to run the original and our algorithms on both real data sets and synthetic data sets. Let $\epsilon \in (0,0.1)$ denote the relative error of the real weight of each edge. The competitive ratio of original \textsc{Greedy} and \textsc{PostponedGreedy} is $\frac{1}{2}$ and $\frac{1}{4}$ respectively. Based on these two original algorithms, we proposed \textsc{FastGreedy} and \textsc{FastPostponedGreedy} algorithms and the competitive ratio of them is $\frac{1 - \epsilon}{2}$ and $\frac{1 - \epsilon}{4}$ respectively. At the same time, our algorithms run faster than the original two algorithms. Given $n$ nodes in $\mathbb{R} ^ d$, we decrease the time complexity from $O(nd)$ to $\widetilde{O}(\epsilon^{-2} \cdot (n + d))$.
A Faster $k$-means++ Algorithm
Nov 28, 2022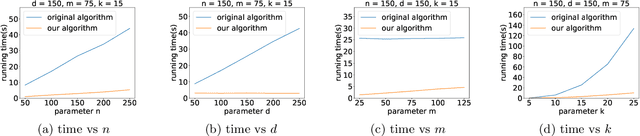

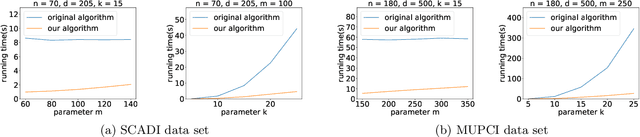
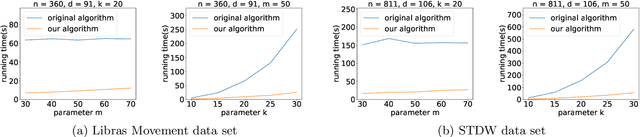
Abstract:K-means++ is an important algorithm to choose initial cluster centers for the k-means clustering algorithm. In this work, we present a new algorithm that can solve the $k$-means++ problem with near optimal running time. Given $n$ data points in $\mathbb{R}^d$, the current state-of-the-art algorithm runs in $\widetilde{O}(k )$ iterations, and each iteration takes $\widetilde{O}(nd k)$ time. The overall running time is thus $\widetilde{O}(n d k^2)$. We propose a new algorithm \textsc{FastKmeans++} that only takes in $\widetilde{O}(nd + nk^2)$ time, in total.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge