The Balanced-Pairwise-Affinities Feature Transform

The Balanced-Pairwise-Affinities (BPA) feature transform is designed to upgrade the features of a set of input items to facilitate downstream matching or grouping related tasks. The transformed set encodes a rich representation of high order relations between the input features. A particular min-cost-max-flow fractional matching problem, whose entropy regularized version can be approximated by an optimal transport (OT) optimization, leads to a transform which is efficient, differentiable, equivariant, parameterless and probabilistically interpretable. While the Sinkhorn OT solver has been adapted extensively in many contexts, we use it differently by minimizing the cost between a set of features to $itself$ and using the transport plan's $rows$ as the new representation. Empirically, the transform is highly effective and flexible in its use and consistently improves networks it is inserted into, in a variety of tasks and training schemes. We demonstrate state-of-the-art results in few-shot classification, unsupervised image clustering and person re-identification. Code is available at \url{github.com/DanielShalam/BPA}.

SeaThru-NeRF: Neural Radiance Fields in Scattering Media

Research on neural radiance fields (NeRFs) for novel view generation is exploding with new models and extensions. However, a question that remains unanswered is what happens in underwater or foggy scenes where the medium strongly influences the appearance of objects. Thus far, NeRF and its variants have ignored these cases. However, since the NeRF framework is based on volumetric rendering, it has inherent capability to account for the medium's effects, once modeled appropriately. We develop a new rendering model for NeRFs in scattering media, which is based on the SeaThru image formation model, and suggest a suitable architecture for learning both scene information and medium parameters. We demonstrate the strength of our method using simulated and real-world scenes, correctly rendering novel photorealistic views underwater. Even more excitingly, we can render clear views of these scenes, removing the medium between the camera and the scene and reconstructing the appearance and depth of far objects, which are severely occluded by the medium. Our code and unique datasets are available on the project's website.

NAN: Noise-Aware NeRFs for Burst-Denoising

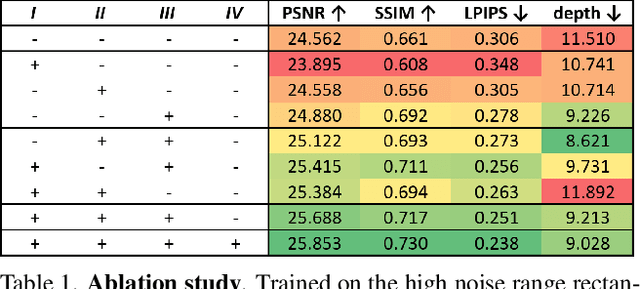
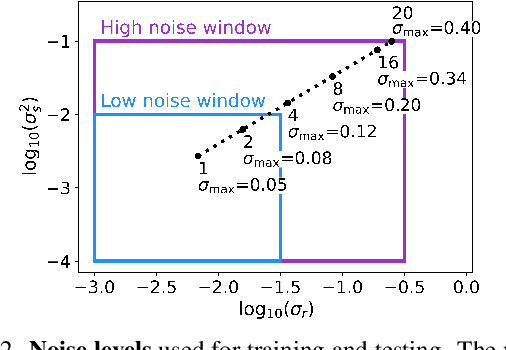
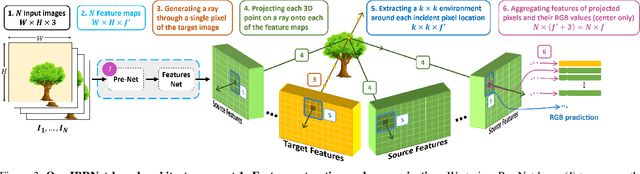
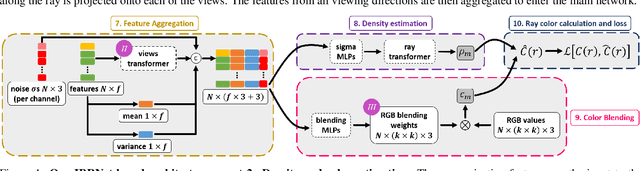
Burst denoising is now more relevant than ever, as computational photography helps overcome sensitivity issues inherent in mobile phones and small cameras. A major challenge in burst-denoising is in coping with pixel misalignment, which was so far handled with rather simplistic assumptions of simple motion, or the ability to align in pre-processing. Such assumptions are not realistic in the presence of large motion and high levels of noise. We show that Neural Radiance Fields (NeRFs), originally suggested for physics-based novel-view rendering, can serve as a powerful framework for burst denoising. NeRFs have an inherent capability of handling noise as they integrate information from multiple images, but they are limited in doing so, mainly since they build on pixel-wise operations which are suitable to ideal imaging conditions. Our approach, termed NAN, leverages inter-view and spatial information in NeRFs to better deal with noise. It achieves state-of-the-art results in burst denoising and is especially successful in coping with large movement and occlusions, under very high levels of noise. With the rapid advances in accelerating NeRFs, it could provide a powerful platform for denoising in challenging environments.

The Self-Optimal-Transport Feature Transform

The Self-Optimal-Transport (SOT) feature transform is designed to upgrade the set of features of a data instance to facilitate downstream matching or grouping related tasks. The transformed set encodes a rich representation of high order relations between the instance features. Distances between transformed features capture their direct original similarity and their third party agreement regarding similarity to other features in the set. A particular min-cost-max-flow fractional matching problem, whose entropy regularized version can be approximated by an optimal transport (OT) optimization, results in our transductive transform which is efficient, differentiable, equivariant, parameterless and probabilistically interpretable. Empirically, the transform is highly effective and flexible in its use, consistently improving networks it is inserted into, in a variety of tasks and training schemes. We demonstrate its merits through the problem of unsupervised clustering and its efficiency and wide applicability for few-shot-classification, with state-of-the-art results, and large-scale person re-identification.

Stabilization of generative adversarial networks via noisy scale-space

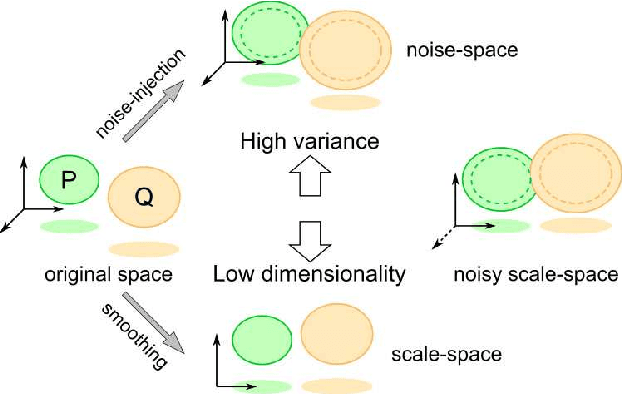
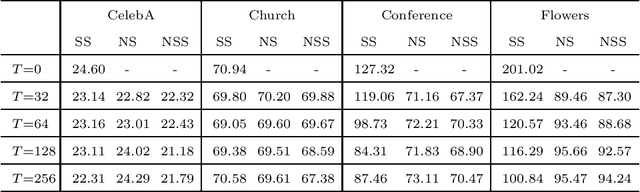
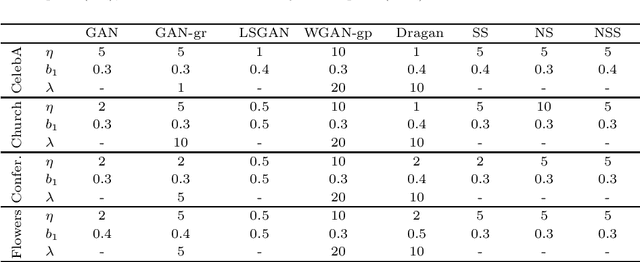
Generative adversarial networks (GAN) is a framework for generating fake data based on given reals but is unstable in the optimization. In order to stabilize GANs, the noise enlarges the overlap of the real and fake distributions at the cost of significant variance. The data smoothing may reduce the dimensionality of data but suppresses the capability of GANs to learn high-frequency information. Based on these observations, we propose a data representation for GANs, called noisy scale-space, that recursively applies the smoothing with noise to data in order to preserve the data variance while replacing high-frequency information by random data, leading to a coarse-to-fine training of GANs. We also present a synthetic data-set using the Hadamard bases that enables us to visualize the true distribution of data. We experiment with a DCGAN with the noise scale-space (NSS-GAN) using major data-sets in which NSS-GAN overtook state-of-the-arts in most cases independent of the image content.

Latent RANSAC

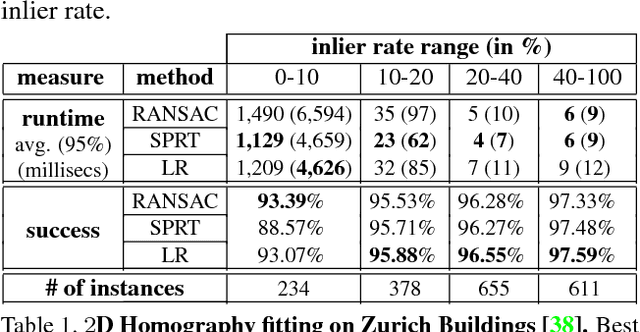
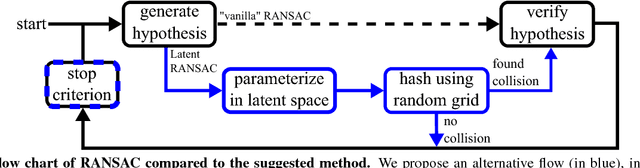
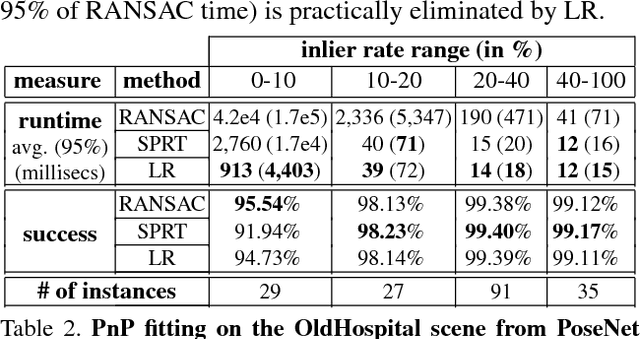
We present a method that can evaluate a RANSAC hypothesis in constant time, i.e. independent of the size of the data. A key observation here is that correct hypotheses are tightly clustered together in the latent parameter domain. In a manner similar to the generalized Hough transform we seek to find this cluster, only that we need as few as two votes for a successful detection. Rapidly locating such pairs of similar hypotheses is made possible by adapting the recent "Random Grids" range-search technique. We only perform the usual (costly) hypothesis verification stage upon the discovery of a close pair of hypotheses. We show that this event rarely happens for incorrect hypotheses, enabling a significant speedup of the RANSAC pipeline. The suggested approach is applied and tested on three robust estimation problems: camera localization, 3D rigid alignment and 2D-homography estimation. We perform rigorous testing on both synthetic and real datasets, demonstrating an improvement in efficiency without a compromise in accuracy. Furthermore, we achieve state-of-the-art 3D alignment results on the challenging "Redwood" loop-closure challenge.

OATM: Occlusion Aware Template Matching by Consensus Set Maximization

We present a novel approach to template matching that is efficient, can handle partial occlusions, and comes with provable performance guarantees. A key component of the method is a reduction that transforms the problem of searching a nearest neighbor among $N$ high-dimensional vectors, to searching neighbors among two sets of order $\sqrt{N}$ vectors, which can be found efficiently using range search techniques. This allows for a quadratic improvement in search complexity, and makes the method scalable in handling large search spaces. The second contribution is a hashing scheme based on consensus set maximization, which allows us to handle occlusions. The resulting scheme can be seen as a randomized hypothesize-and-test algorithm, which is equipped with guarantees regarding the number of iterations required for obtaining an optimal solution with high probability. The predicted matching rates are validated empirically and the algorithm shows a significant improvement over the state-of-the-art in both speed and robustness to occlusions.

Deleting and Testing Forbidden Patterns in Multi-Dimensional Arrays

Understanding the local behaviour of structured multi-dimensional data is a fundamental problem in various areas of computer science. As the amount of data is often huge, it is desirable to obtain sublinear time algorithms, and specifically property testers, to understand local properties of the data. We focus on the natural local problem of testing pattern freeness: given a large $d$-dimensional array $A$ and a fixed $d$-dimensional pattern $P$ over a finite alphabet, we say that $A$ is $P$-free if it does not contain a copy of the forbidden pattern $P$ as a consecutive subarray. The distance of $A$ to $P$-freeness is the fraction of entries of $A$ that need to be modified to make it $P$-free. For any $\epsilon \in [0,1]$ and any large enough pattern $P$ over any alphabet, other than a very small set of exceptional patterns, we design a tolerant tester that distinguishes between the case that the distance is at least $\epsilon$ and the case that it is at most $a_d \epsilon$, with query complexity and running time $c_d \epsilon^{-1}$, where $a_d < 1$ and $c_d$ depend only on $d$. To analyze the testers we establish several combinatorial results, including the following $d$-dimensional modification lemma, which might be of independent interest: for any large enough pattern $P$ over any alphabet (excluding a small set of exceptional patterns for the binary case), and any array $A$ containing a copy of $P$, one can delete this copy by modifying one of its locations without creating new $P$-copies in $A$. Our results address an open question of Fischer and Newman, who asked whether there exist efficient testers for properties related to tight substructures in multi-dimensional structured data. They serve as a first step towards a general understanding of local properties of multi-dimensional arrays, as any such property can be characterized by a fixed family of forbidden patterns.