Advancing Compositional Awareness in CLIP with Efficient Fine-Tuning

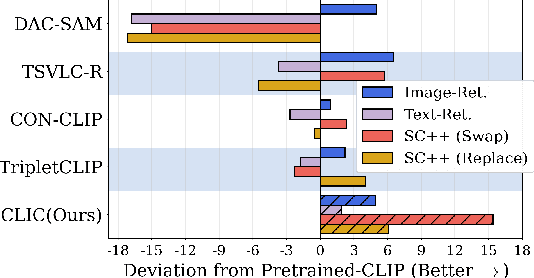
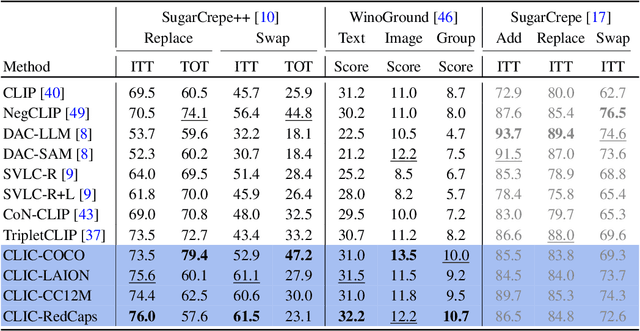
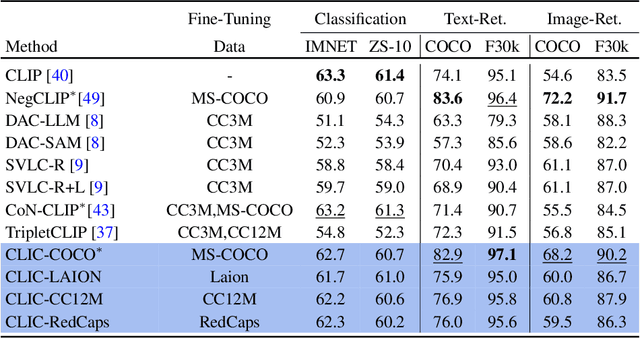
Vision-language models like CLIP have demonstrated remarkable zero-shot capabilities in classification and retrieval. However, these models often struggle with compositional reasoning - the ability to understand the relationships between concepts. A recent benchmark, SugarCrepe++, reveals that previous works on improving compositionality have mainly improved lexical sensitivity but neglected semantic understanding. In addition, downstream retrieval performance often deteriorates, although one would expect that improving compositionality should enhance retrieval. In this work, we introduce CLIC (Compositionally-aware Learning in CLIP), a fine-tuning method based on a novel training technique combining multiple images and their associated captions. CLIC improves compositionality across architectures as well as differently pre-trained CLIP models, both in terms of lexical and semantic understanding, and achieves consistent gains in retrieval performance. This even applies to the recent CLIPS, which achieves SOTA retrieval performance. Nevertheless, the short fine-tuning with CLIC leads to an improvement in retrieval and to the best compositional CLIP model on SugarCrepe++. All our models and code are available at https://clic-compositional-clip.github.io

Bias of Stochastic Gradient Descent or the Architecture: Disentangling the Effects of Overparameterization of Neural Networks

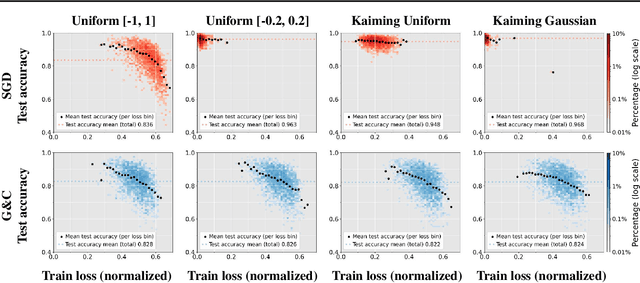
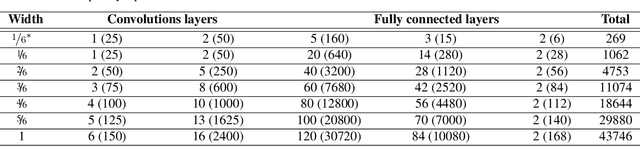
Neural networks typically generalize well when fitting the data perfectly, even though they are heavily overparameterized. Many factors have been pointed out as the reason for this phenomenon, including an implicit bias of stochastic gradient descent (SGD) and a possible simplicity bias arising from the neural network architecture. The goal of this paper is to disentangle the factors that influence generalization stemming from optimization and architectural choices by studying random and SGD-optimized networks that achieve zero training error. We experimentally show, in the low sample regime, that overparameterization in terms of increasing width is beneficial for generalization, and this benefit is due to the bias of SGD and not due to an architectural bias. In contrast, for increasing depth, overparameterization is detrimental for generalization, but random and SGD-optimized networks behave similarly, so this can be attributed to an architectural bias. For more information, see https://bias-sgd-or-architecture.github.io .

SeaThru-NeRF: Neural Radiance Fields in Scattering Media

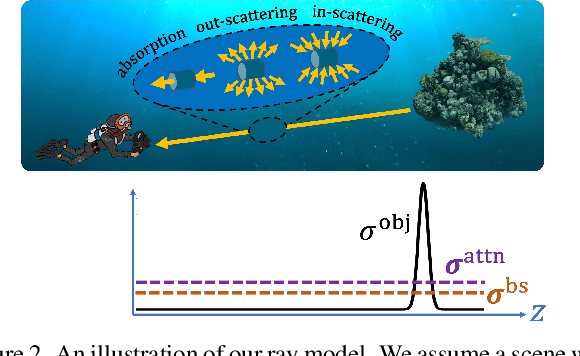
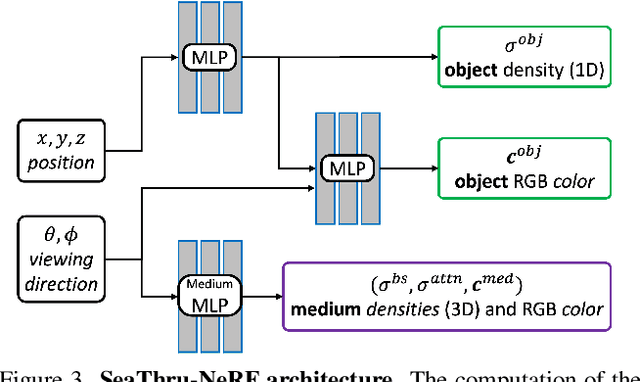
Research on neural radiance fields (NeRFs) for novel view generation is exploding with new models and extensions. However, a question that remains unanswered is what happens in underwater or foggy scenes where the medium strongly influences the appearance of objects. Thus far, NeRF and its variants have ignored these cases. However, since the NeRF framework is based on volumetric rendering, it has inherent capability to account for the medium's effects, once modeled appropriately. We develop a new rendering model for NeRFs in scattering media, which is based on the SeaThru image formation model, and suggest a suitable architecture for learning both scene information and medium parameters. We demonstrate the strength of our method using simulated and real-world scenes, correctly rendering novel photorealistic views underwater. Even more excitingly, we can render clear views of these scenes, removing the medium between the camera and the scene and reconstructing the appearance and depth of far objects, which are severely occluded by the medium. Our code and unique datasets are available on the project's website.

Metalearning Linear Bandits by Prior Update

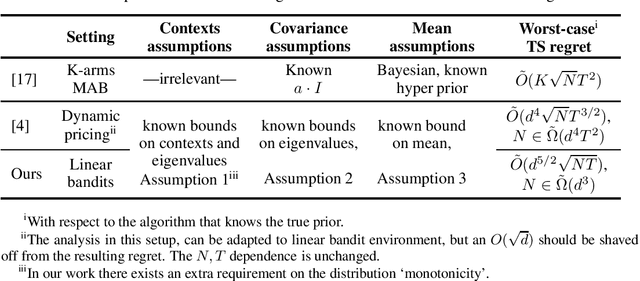
Fully Bayesian approaches to sequential decision-making assume that problem parameters are generated from a known prior, while in practice, such information is often lacking, and needs to be estimated through learning. This problem is exacerbated in decision-making setups with partial information, where using a misspecified prior may lead to poor exploration and inferior performance. In this work we prove, in the context of stochastic linear bandits and Gaussian priors, that as long as the prior estimate is sufficiently close to the true prior, the performance of an algorithm that uses the misspecified prior is close to that of the algorithm that uses the true prior. Next, we address the task of learning the prior through metalearning, where a learner updates its estimate of the prior across multiple task instances in order to improve performance on future tasks. The estimated prior is then updated within each task based on incoming observations, while actions are selected in order to maximize expected reward. In this work we apply this scheme within a linear bandit setting, and provide algorithms and regret bounds, demonstrating its effectiveness, as compared to an algorithm that knows the correct prior. Our results hold for a broad class of algorithms, including, for example, Thompson Sampling and Information Directed Sampling.