Metalearning Linear Bandits by Prior Update
Paper and Code
Jul 12, 2021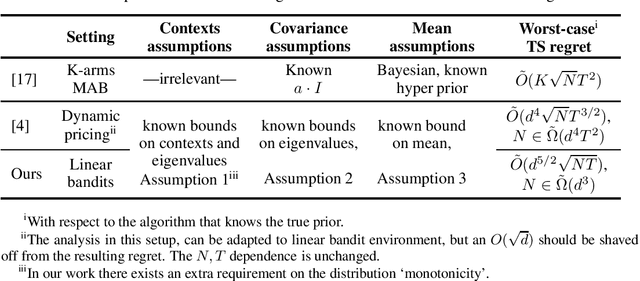
Fully Bayesian approaches to sequential decision-making assume that problem parameters are generated from a known prior, while in practice, such information is often lacking, and needs to be estimated through learning. This problem is exacerbated in decision-making setups with partial information, where using a misspecified prior may lead to poor exploration and inferior performance. In this work we prove, in the context of stochastic linear bandits and Gaussian priors, that as long as the prior estimate is sufficiently close to the true prior, the performance of an algorithm that uses the misspecified prior is close to that of the algorithm that uses the true prior. Next, we address the task of learning the prior through metalearning, where a learner updates its estimate of the prior across multiple task instances in order to improve performance on future tasks. The estimated prior is then updated within each task based on incoming observations, while actions are selected in order to maximize expected reward. In this work we apply this scheme within a linear bandit setting, and provide algorithms and regret bounds, demonstrating its effectiveness, as compared to an algorithm that knows the correct prior. Our results hold for a broad class of algorithms, including, for example, Thompson Sampling and Information Directed Sampling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge