Diffusion Models for Cayley Graphs

We review the problem of finding paths in Cayley graphs of groups and group actions, using the Rubik's cube as an example, and we list several more examples of significant mathematical interest. We then show how to formulate these problems in the framework of diffusion models. The exploration of the graph is carried out by the forward process, while finding the target nodes is done by the inverse backward process. This systematizes the discussion and suggests many generalizations. To improve exploration, we propose a ``reversed score'' ansatz which substantially improves over previous comparable algorithms.

Mathematical Data Science

Can machine learning help discover new mathematical structures? In this article we discuss an approach to doing this which one can call "mathematical data science". In this paradigm, one studies mathematical objects collectively rather than individually, by creating datasets and doing machine learning experiments and interpretations. After an overview, we present two case studies: murmurations in number theory and loadings of partitions related to Kronecker coefficients in representation theory and combinatorics.

Progress in Artificial Intelligence and its Determinants

We study long-run progress in artificial intelligence in a quantitative way. Many measures, including traditional ones such as patents and publications, machine learning benchmarks, and a new Aggregate State of the Art in ML (or ASOTA) Index we have constructed from these, show exponential growth at roughly constant rates over long periods. Production of patents and publications doubles every ten years, by contrast with the growth of computing resources driven by Moore's Law, roughly a doubling every two years. We argue that the input of AI researchers is also crucial and its contribution can be objectively estimated. Consequently, we give a simple argument that explains the 5:1 relation between these two rates. We then discuss the application of this argument to different output measures and compare our analyses with predictions based on machine learning scaling laws proposed in existing literature. Our quantitative framework facilitates understanding, predicting, and modulating the development of these important technologies.

Large Language Models

Artificial intelligence is making spectacular progress, and one of the best examples is the development of large language models (LLMs) such as OpenAI's GPT series. In these lectures, written for readers with a background in mathematics or physics, we give a brief history and survey of the state of the art, and describe the underlying transformer architecture in detail. We then explore some current ideas on how LLMs work and how models trained to predict the next word in a text are able to perform other tasks displaying intelligence.

What is Learned in Knowledge Graph Embeddings?

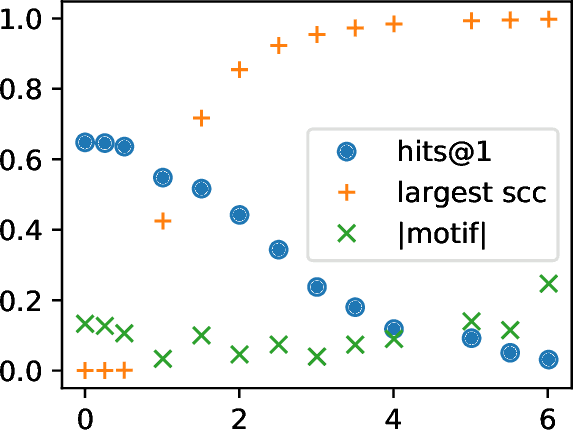
A knowledge graph (KG) is a data structure which represents entities and relations as the vertices and edges of a directed graph with edge types. KGs are an important primitive in modern machine learning and artificial intelligence. Embedding-based models, such as the seminal TransE [Bordes et al., 2013] and the recent PairRE [Chao et al., 2020] are among the most popular and successful approaches for representing KGs and inferring missing edges (link completion). Their relative success is often credited in the literature to their ability to learn logical rules between the relations. In this work, we investigate whether learning rules between relations is indeed what drives the performance of embedding-based methods. We define motif learning and two alternative mechanisms, network learning (based only on the connectivity of the KG, ignoring the relation types), and unstructured statistical learning (ignoring the connectivity of the graph). Using experiments on synthetic KGs, we show that KG models can learn motifs and how this ability is degraded by non-motif (noise) edges. We propose tests to distinguish the contributions of the three mechanisms to performance, and apply them to popular KG benchmarks. We also discuss an issue with the standard performance testing protocol and suggest an improvement. To appear in the proceedings of Complex Networks 2021.