Kyu-Hwan Lee
From Black Box to Bijection: Interpreting Machine Learning to Build a Zeta Map Algorithm
Nov 16, 2025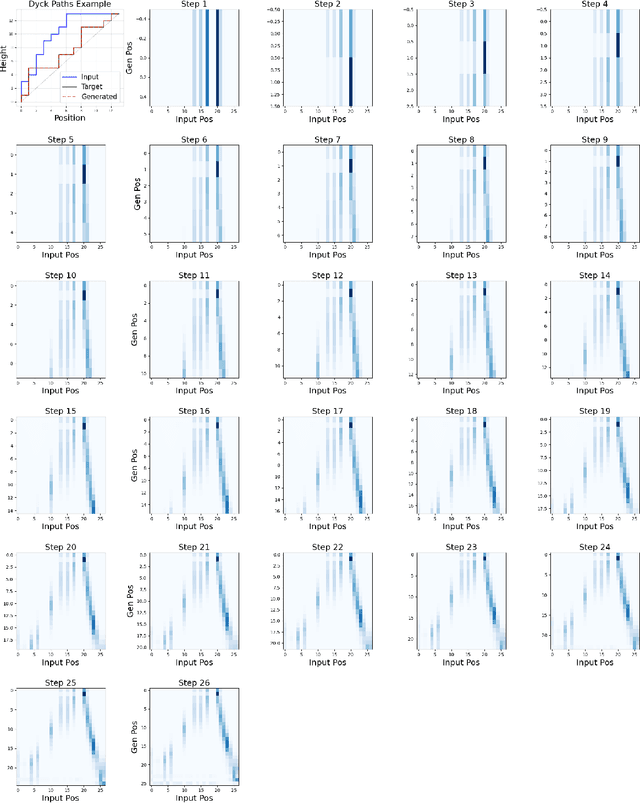
Abstract:There is a large class of problems in algebraic combinatorics which can be distilled into the same challenge: construct an explicit combinatorial bijection. Traditionally, researchers have solved challenges like these by visually inspecting the data for patterns, formulating conjectures, and then proving them. But what is to be done if patterns fail to emerge until the data grows beyond human scale? In this paper, we propose a new workflow for discovering combinatorial bijections via machine learning. As a proof of concept, we train a transformer on paired Dyck paths and use its learned attention patterns to derive a new algorithmic description of the zeta map, which we call the \textit{Scaffolding Map}.
Interpretable Machine Learning for Kronecker Coefficients
Feb 17, 2025Abstract:We analyze the saliency of neural networks and employ interpretable machine learning models to predict whether the Kronecker coefficients of the symmetric group are zero or not. Our models use triples of partitions as input features, as well as b-loadings derived from the principal component of an embedding that captures the differences between partitions. Across all approaches, we achieve an accuracy of approximately 83% and derive explicit formulas for a decision function in terms of b-loadings. Additionally, we develop transformer-based models for prediction, achieving the highest reported accuracy of over 99%.
Mathematical Data Science
Feb 12, 2025Abstract:Can machine learning help discover new mathematical structures? In this article we discuss an approach to doing this which one can call "mathematical data science". In this paradigm, one studies mathematical objects collectively rather than individually, by creating datasets and doing machine learning experiments and interpretations. After an overview, we present two case studies: murmurations in number theory and loadings of partitions related to Kronecker coefficients in representation theory and combinatorics.
Learning Fricke signs from Maass form Coefficients
Jan 03, 2025



Abstract:In this paper, we conduct a data-scientific investigation of Maass forms. We find that averaging the Fourier coefficients of Maass forms with the same Fricke sign reveals patterns analogous to the recently discovered "murmuration" phenomenon, and that these patterns become more pronounced when parity is incorporated as an additional feature. Approximately 43% of the forms in our dataset have an unknown Fricke sign. For the remaining forms, we employ Linear Discriminant Analysis (LDA) to machine learn their Fricke sign, achieving 96% (resp. 94%) accuracy for forms with even (resp. odd) parity. We apply the trained LDA model to forms with unknown Fricke signs to make predictions. The average values based on the predicted Fricke signs are computed and compared to those for forms with known signs to verify the reasonableness of the predictions. Additionally, a subset of these predictions is evaluated against heuristic guesses provided by Hejhal's algorithm, showing a match approximately 95% of the time. We also use neural networks to obtain results comparable to those from the LDA model.
Machine Learning Mutation-Acyclicity of Quivers
Nov 06, 2024


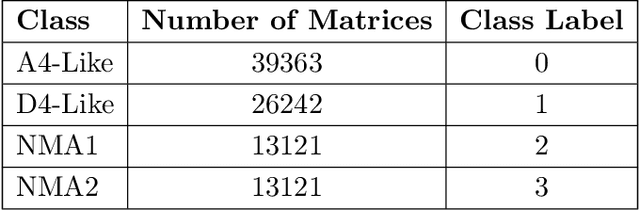
Abstract:Machine learning (ML) has emerged as a powerful tool in mathematical research in recent years. This paper applies ML techniques to the study of quivers--a type of directed multigraph with significant relevance in algebra, combinatorics, computer science, and mathematical physics. Specifically, we focus on the challenging problem of determining the mutation-acyclicity of a quiver on 4 vertices, a property that is pivotal since mutation-acyclicity is often a necessary condition for theorems involving path algebras and cluster algebras. Although this classification is known for quivers with at most 3 vertices, little is known about quivers on more than 3 vertices. We give a computer-assisted proof of a theorem to prove that mutation-acyclicity is decidable for quivers on 4 vertices with edge weight at most 2. By leveraging neural networks (NNs) and support vector machines (SVMs), we then accurately classify more general 4-vertex quivers as mutation-acyclic or non-mutation-acyclic. Our results demonstrate that ML models can efficiently detect mutation-acyclicity, providing a promising computational approach to this combinatorial problem, from which the trained SVM equation provides a starting point to guide future theoretical development.
Machine-Learning Kronecker Coefficients
Jun 07, 2023Abstract:The Kronecker coefficients are the decomposition multiplicities of the tensor product of two irreducible representations of the symmetric group. Unlike the Littlewood--Richardson coefficients, which are the analogues for the general linear group, there is no known combinatorial description of the Kronecker coefficients, and it is an NP-hard problem to decide whether a given Kronecker coefficient is zero or not. In this paper, we show that standard machine-learning algorithms such as Nearest Neighbors, Convolutional Neural Networks and Gradient Boosting Decision Trees may be trained to predict whether a given Kronecker coefficient is zero or not. Our results show that a trained machine can efficiently perform this binary classification with high accuracy ($\approx 0.98$).
Machine Learning Class Numbers of Real Quadratic Fields
Sep 19, 2022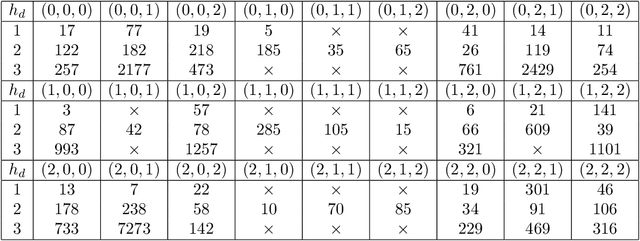
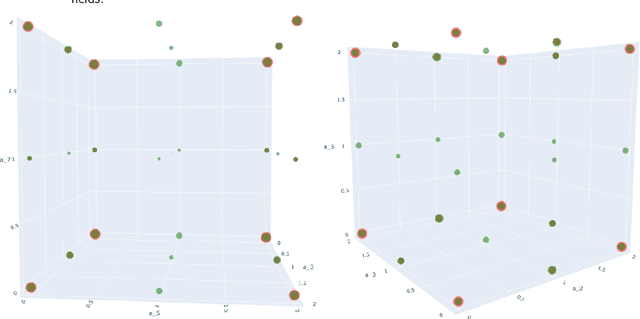
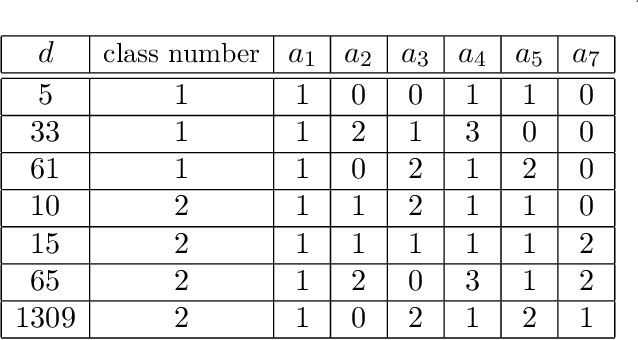
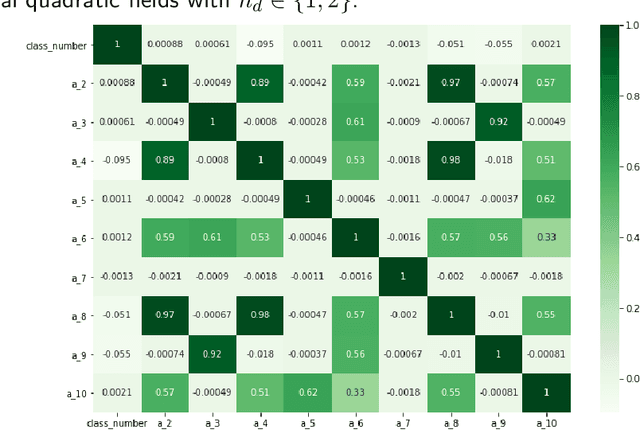
Abstract:We implement and interpret various supervised learning experiments involving real quadratic fields with class numbers 1, 2 and 3. We quantify the relative difficulties in separating class numbers of matching/different parity from a data-scientific perspective, apply the methodology of feature analysis and principal component analysis, and use symbolic classification to develop machine-learned formulas for class numbers 1, 2 and 3 that apply to our dataset.
Murmurations of elliptic curves
Apr 21, 2022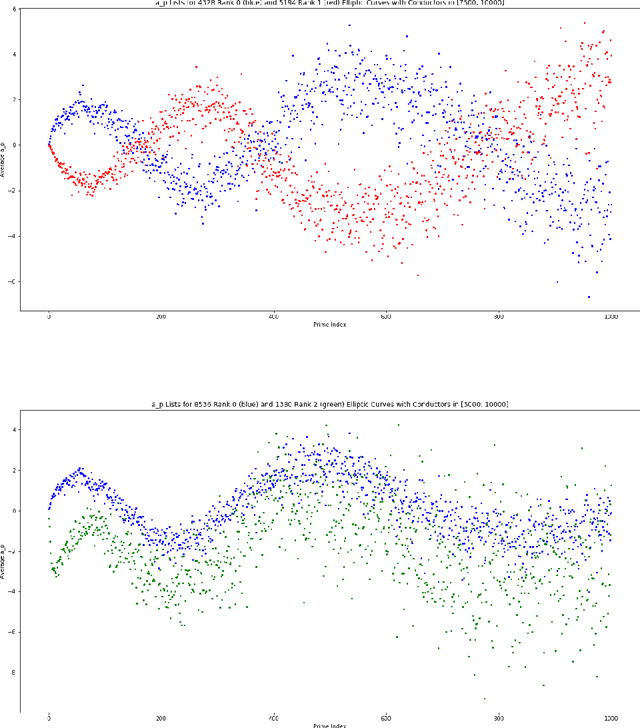
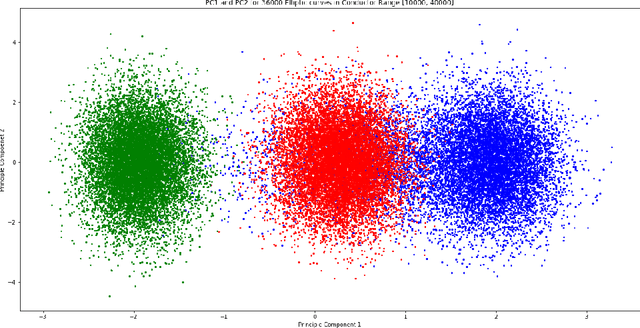
Abstract:We investigate the average value of the $p$th Dirichlet coefficients of elliptic curves for a prime p in a fixed conductor range with given rank. Plotting this average yields a striking oscillating pattern, the details of which vary with the rank. Based on this observation, we perform various data-scientific experiments with the goal of classifying elliptic curves according to their ranks.
Machine-Learning Arithmetic Curves
Dec 07, 2020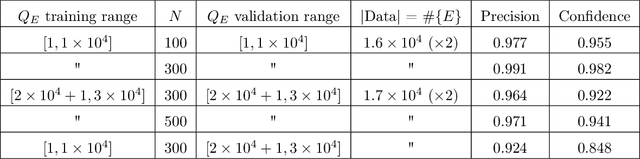
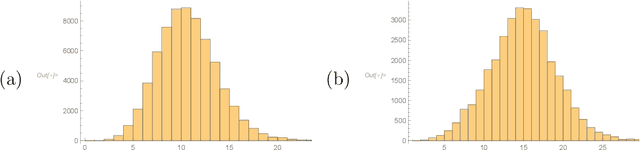
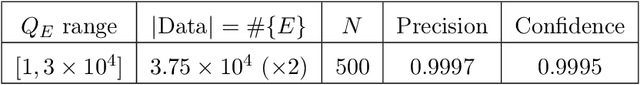
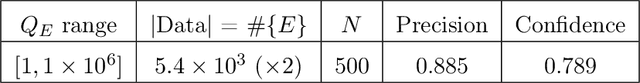
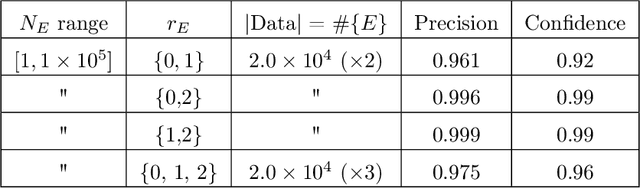
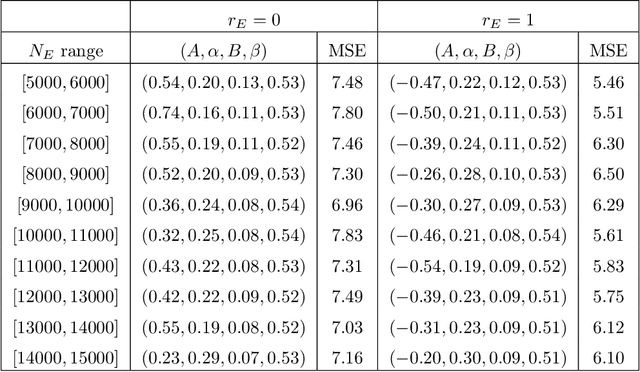
Abstract:We show that standard machine-learning algorithms may be trained to predict certain invariants of low genus arithmetic curves. Using datasets of size around one hundred thousand, we demonstrate the utility of machine-learning in classification problems pertaining to the BSD invariants of an elliptic curve (including its rank and torsion subgroup), and the analogous invariants of a genus 2 curve. Our results show that a trained machine can efficiently classify curves according to these invariants with high accuracies (>0.97). For problems such as distinguishing between torsion orders, and the recognition of integral points, the accuracies can reach 0.998.
Machine-Learning Number Fields
Nov 17, 2020


Abstract:We show that standard machine-learning algorithms may be trained to predict certain invariants of algebraic number fields to high accuracy. A random-forest classifier that is trained on finitely many Dedekind zeta coefficients is able to distinguish between real quadratic fields with class number 1 and 2, to 0.96 precision. Furthermore, the classifier is able to extrapolate to fields with discriminant outside the range of the training data. When trained on the coefficients of defining polynomials for Galois extensions of degrees 2, 6, and 8, a logistic regression classifier can distinguish between Galois groups and predict the ranks of unit groups with precision >0.97.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge