A Triumvirate of AI Driven Theoretical Discovery

Recent years have seen the dramatic rise of the usage of AI algorithms in pure mathematics and fundamental sciences such as theoretical physics. This is perhaps counter-intuitive since mathematical sciences require the rigorous definitions, derivations, and proofs, in contrast to the experimental sciences which rely on the modelling of data with error-bars. In this Perspective, we categorize the approaches to mathematical discovery as "top-down", "bottom-up" and "meta-mathematics", as inspired by historical examples. We review some of the progress over the last few years, comparing and contrasting both the advances and the short-comings in each approach. We argue that while the theorist is in no way in danger of being replaced by AI in the near future, the hybrid of human expertise and AI algorithms will become an integral part of theoretical discovery.

Learning 3-Manifold Triangulations

Real 3-manifold triangulations can be uniquely represented by isomorphism signatures. Databases of these isomorphism signatures are generated for a variety of 3-manifolds and knot complements, using SnapPy and Regina, then these language-like inputs are used to train various machine learning architectures to differentiate the manifolds, as well as their Dehn surgeries, via their triangulations. Gradient saliency analysis then extracts key parts of this language-like encoding scheme from the trained models. The isomorphism signature databases are taken from the 3-manifolds' Pachner graphs, which are also generated in bulk for some selected manifolds of focus and for the subset of the SnapPy orientable cusped census with $<8$ initial tetrahedra. These Pachner graphs are further analysed through the lens of network science to identify new structure in the triangulation representation; in particular for the hyperbolic case, a relation between the length of the shortest geodesic (systole) and the size of the Pachner graph's ball is observed.

Learning to be Simple

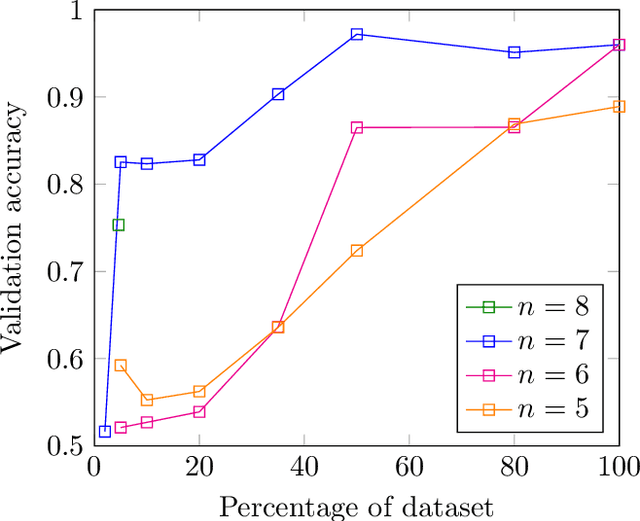
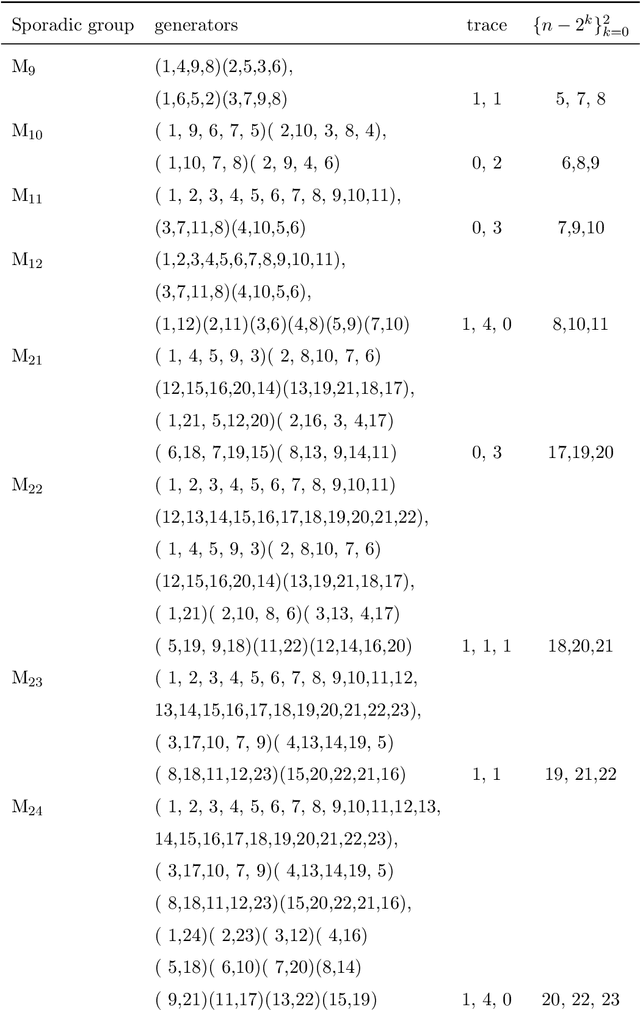
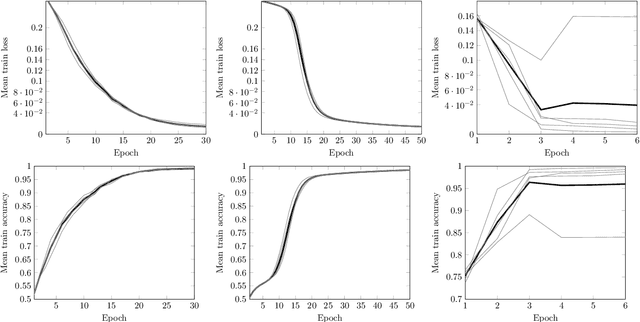
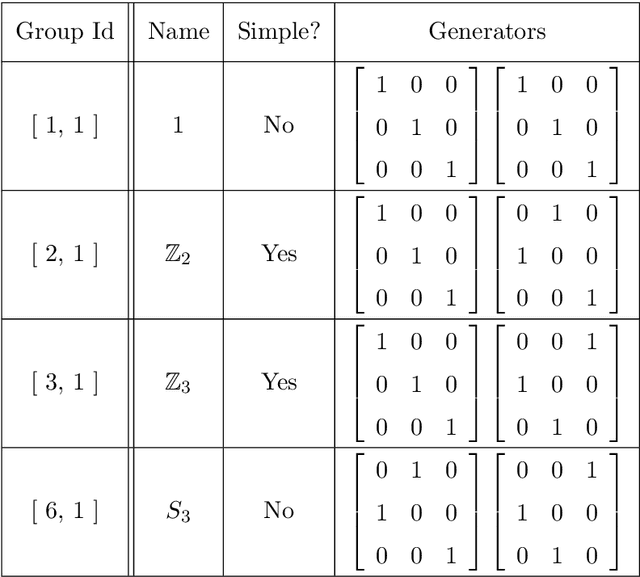
In this work we employ machine learning to understand structured mathematical data involving finite groups and derive a theorem about necessary properties of generators of finite simple groups. We create a database of all 2-generated subgroups of the symmetric group on n-objects and conduct a classification of finite simple groups among them using shallow feed-forward neural networks. We show that this neural network classifier can decipher the property of simplicity with varying accuracies depending on the features. Our neural network model leads to a natural conjecture concerning the generators of a finite simple group. We subsequently prove this conjecture. This new toy theorem comments on the necessary properties of generators of finite simple groups. We show this explicitly for a class of sporadic groups for which the result holds. Our work further makes the case for a machine motivated study of algebraic structures in pure mathematics and highlights the possibility of generating new conjectures and theorems in mathematics with the aid of machine learning.

Machine Learning Clifford invariants of ADE Coxeter elements

There has been recent interest in novel Clifford geometric invariants of linear transformations. This motivates the investigation of such invariants for a certain type of geometric transformation of interest in the context of root systems, reflection groups, Lie groups and Lie algebras: the Coxeter transformations. We perform exhaustive calculations of all Coxeter transformations for $A_8$, $D_8$ and $E_8$ for a choice of basis of simple roots and compute their invariants, using high-performance computing. This computational algebra paradigm generates a dataset that can then be mined using techniques from data science such as supervised and unsupervised machine learning. In this paper we focus on neural network classification and principal component analysis. Since the output -- the invariants -- is fully determined by the choice of simple roots and the permutation order of the corresponding reflections in the Coxeter element, we expect huge degeneracy in the mapping. This provides the perfect setup for machine learning, and indeed we see that the datasets can be machine learned to very high accuracy. This paper is a pump-priming study in experimental mathematics using Clifford algebras, showing that such Clifford algebraic datasets are amenable to machine learning, and shedding light on relationships between these novel and other well-known geometric invariants and also giving rise to analytic results.

Towards Quantum Advantage on Noisy Quantum Computers

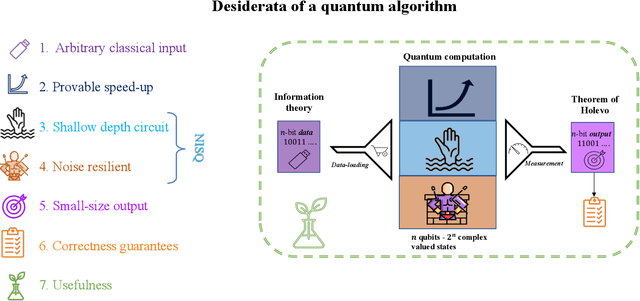
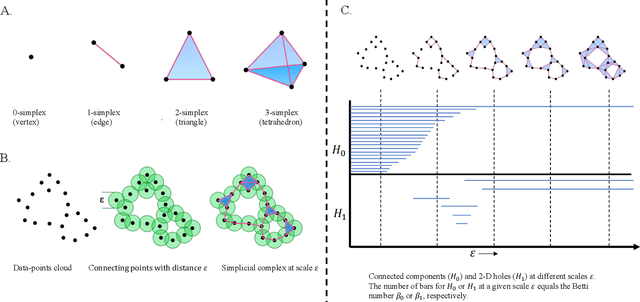
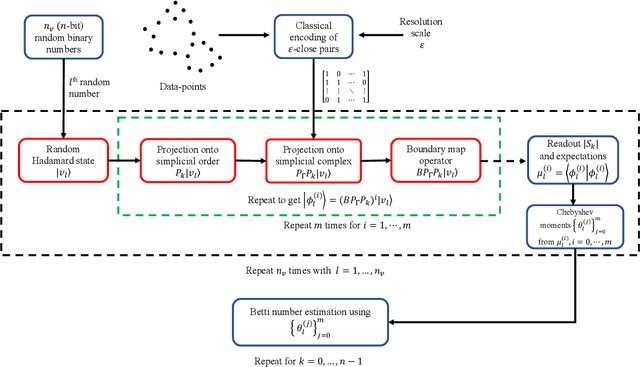
Topological data analysis (TDA) is a powerful technique for extracting complex and valuable shape-related summaries of high-dimensional data. However, the computational demands of classical TDA algorithms are exorbitant, and quickly become impractical for high-order characteristics. Quantum computing promises exponential speedup for certain problems. Yet, many existing quantum algorithms with notable asymptotic speedups require a degree of fault tolerance that is currently unavailable. In this paper, we present NISQ-TDA, the first fully implemented end-to-end quantum machine learning algorithm needing only a linear circuit-depth, that is applicable to non-handcrafted high-dimensional classical data, with potential speedup under stringent conditions. The algorithm neither suffers from the data-loading problem nor does it need to store the input data on the quantum computer explicitly. Our approach includes three key innovations: (a) an efficient realization of the full boundary operator as a sum of Pauli operators; (b) a quantum rejection sampling and projection approach to restrict a uniform superposition to the simplices of the desired order in the complex; and (c) a stochastic rank estimation method to estimate the topological features in the form of approximate Betti numbers. We present theoretical results that establish additive error guarantees for NISQ-TDA, and the circuit and computational time and depth complexities for exponentially scaled output estimates, up to the error tolerance. The algorithm was successfully executed on quantum computing devices, as well as on noisy quantum simulators, applied to small datasets. Preliminary empirical results suggest that the algorithm is robust to noise.

Machine Learning Class Numbers of Real Quadratic Fields

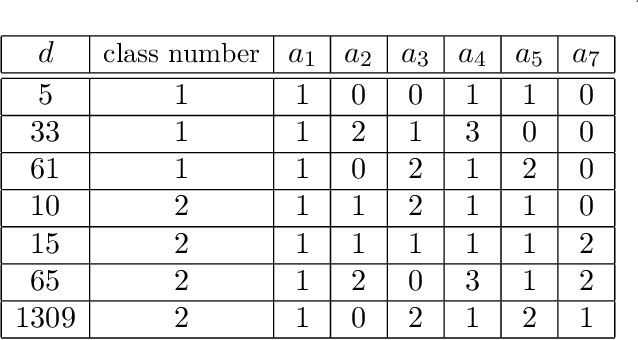
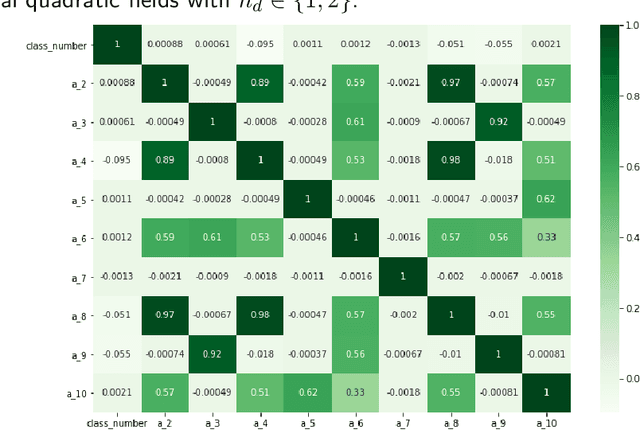
We implement and interpret various supervised learning experiments involving real quadratic fields with class numbers 1, 2 and 3. We quantify the relative difficulties in separating class numbers of matching/different parity from a data-scientific perspective, apply the methodology of feature analysis and principal component analysis, and use symbolic classification to develop machine-learned formulas for class numbers 1, 2 and 3 that apply to our dataset.

Machine Learning Algebraic Geometry for Physics

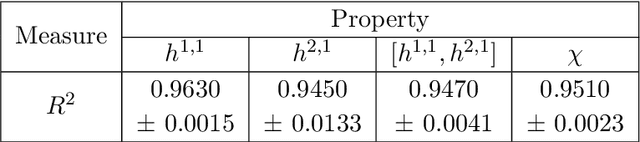
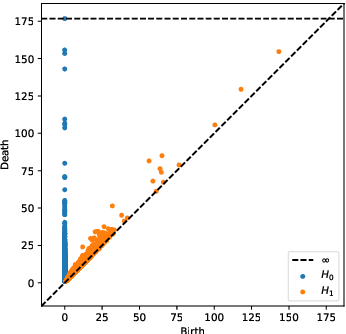
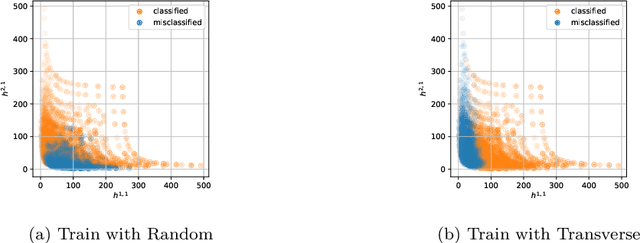
We review some recent applications of machine learning to algebraic geometry and physics. Since problems in algebraic geometry can typically be reformulated as mappings between tensors, this makes them particularly amenable to supervised learning. Additionally, unsupervised methods can provide insight into the structure of such geometrical data. At the heart of this programme is the question of how geometry can be machine learned, and indeed how AI helps one to do mathematics. This is a chapter contribution to the book Machine learning and Algebraic Geometry, edited by A. Kasprzyk et al.

Murmurations of elliptic curves

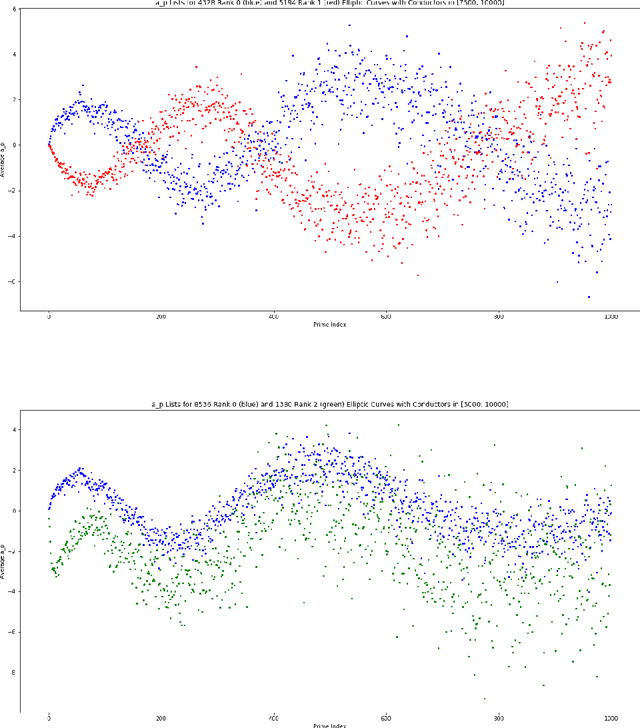
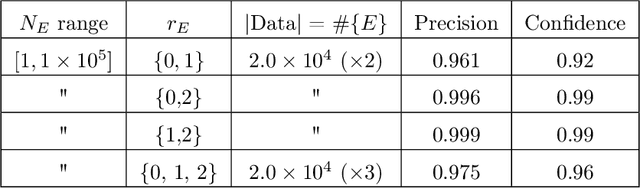
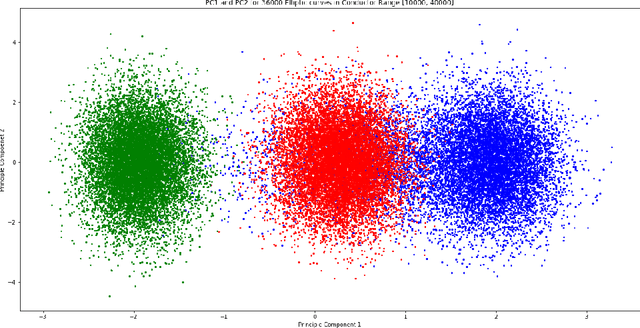
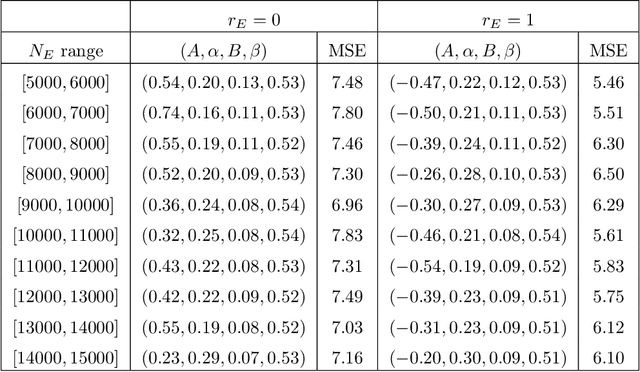
We investigate the average value of the $p$th Dirichlet coefficients of elliptic curves for a prime p in a fixed conductor range with given rank. Plotting this average yields a striking oscillating pattern, the details of which vary with the rank. Based on this observation, we perform various data-scientific experiments with the goal of classifying elliptic curves according to their ranks.

Cluster Algebras: Network Science and Machine Learning

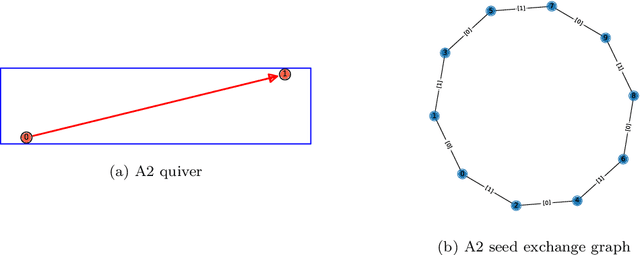
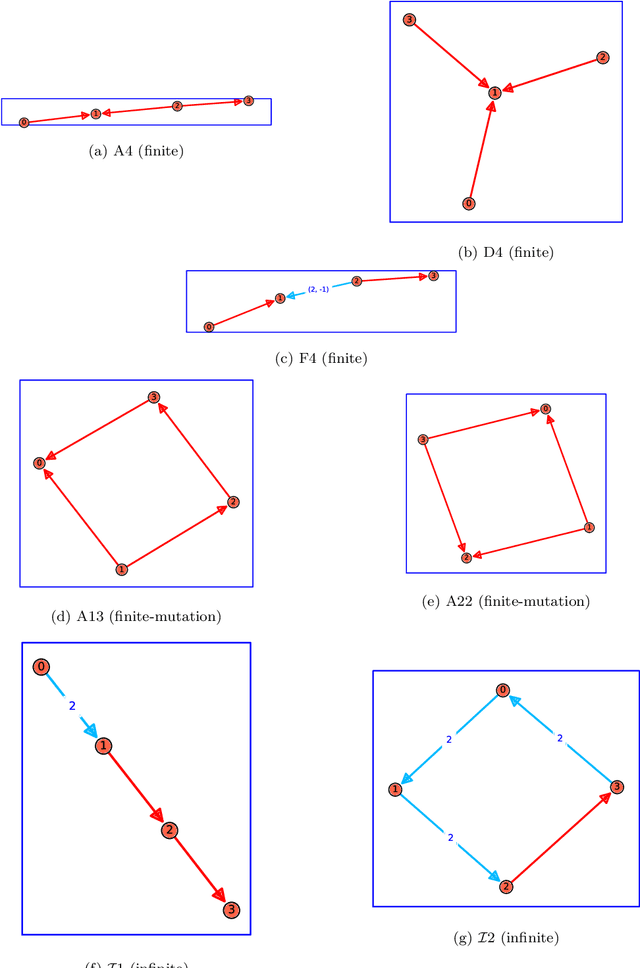
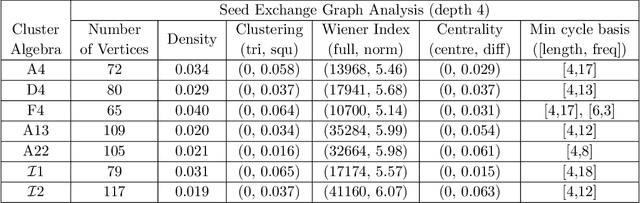
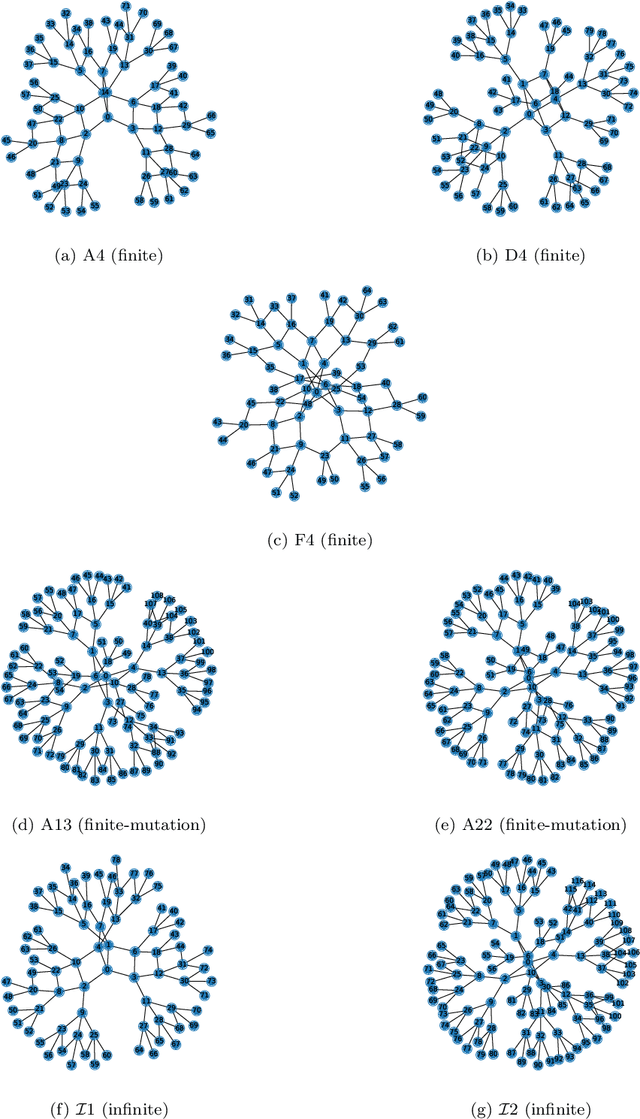
Cluster algebras have recently become an important player in mathematics and physics. In this work, we investigate them through the lens of modern data science, specifically with techniques from network science and machine-learning. Network analysis methods are applied to the exchange graphs for cluster algebras of varying mutation types. The analysis indicates that when the graphs are represented without identifying by permutation equivalence between clusters an elegant symmetry emerges in the quiver exchange graph embedding. The ratio between number of seeds and number of quivers associated to this symmetry is computed for finite Dynkin type algebras up to rank 5, and conjectured for higher ranks. Simple machine learning techniques successfully learn to differentiate cluster algebras from their seeds. The learning performance exceeds 0.9 accuracies between algebras of the same mutation type and between types, as well as relative to artificially generated data.

From the String Landscape to the Mathematical Landscape: a Machine-Learning Outlook

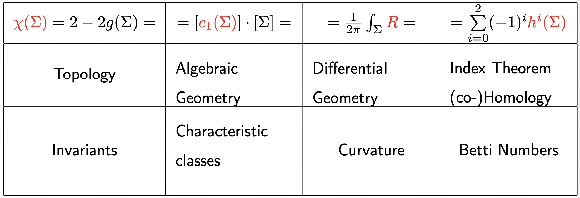
We review the recent programme of using machine-learning to explore the landscape of mathematical problems. With this paradigm as a model for human intuition - complementary to and in contrast with the more formalistic approach of automated theorem proving - we highlight some experiments on how AI helps with conjecture formulation, pattern recognition and computation.