Jiakang Bao
Machine Learning Algebraic Geometry for Physics
Apr 21, 2022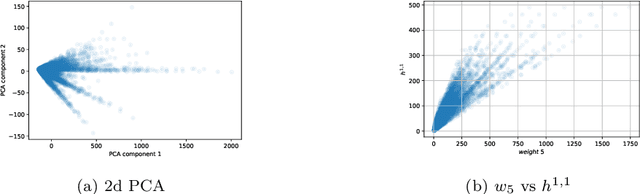
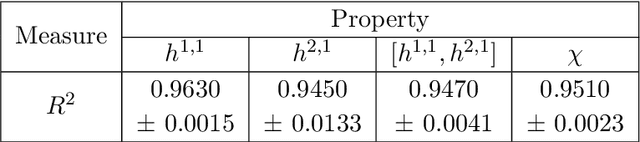
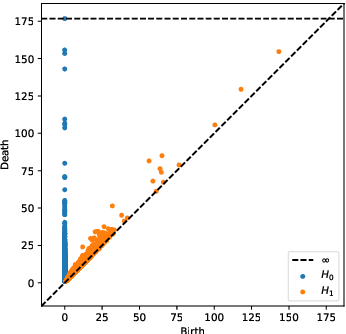
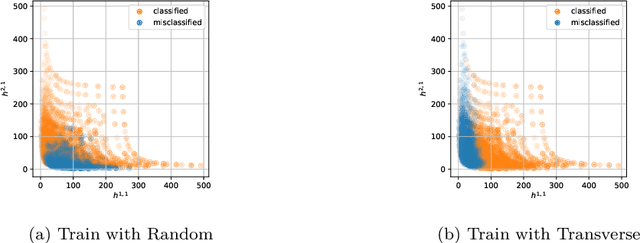
Abstract:We review some recent applications of machine learning to algebraic geometry and physics. Since problems in algebraic geometry can typically be reformulated as mappings between tensors, this makes them particularly amenable to supervised learning. Additionally, unsupervised methods can provide insight into the structure of such geometrical data. At the heart of this programme is the question of how geometry can be machine learned, and indeed how AI helps one to do mathematics. This is a chapter contribution to the book Machine learning and Algebraic Geometry, edited by A. Kasprzyk et al.
Neurons on Amoebae
Jun 07, 2021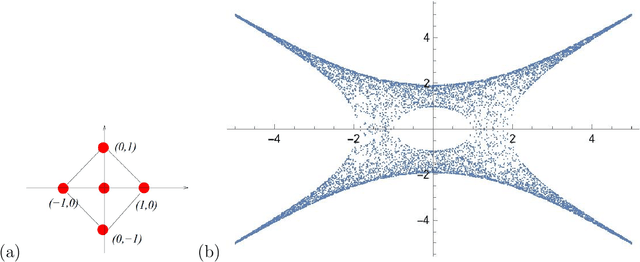

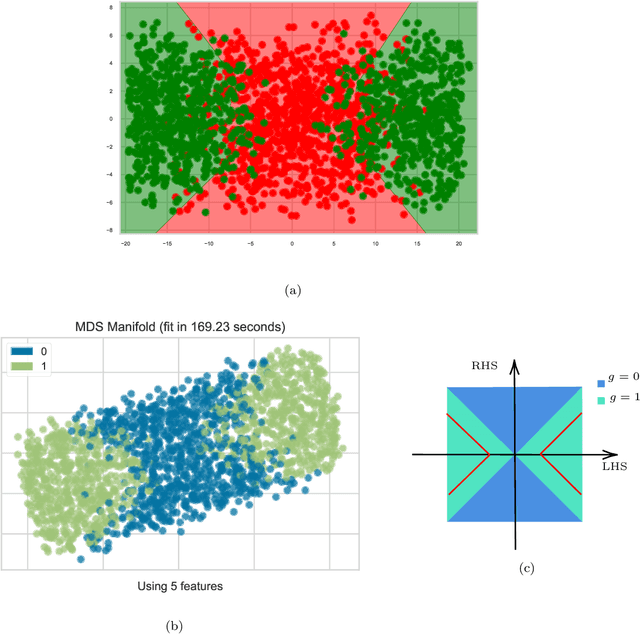

Abstract:We apply methods of machine-learning, such as neural networks, manifold learning and image processing, in order to study amoebae in algebraic geometry and string theory. With the help of embedding manifold projection, we recover complicated conditions obtained from so-called lopsidedness. For certain cases (e.g. lopsided amoeba with positive coefficients for $F_0$), it could even reach $\sim99\%$ accuracy. Using weights and biases, we also find good approximations to determine the genus for an amoeba at lower computational cost. In general, the models could easily predict the genus with over $90\%$ accuracies. With similar techniques, we also investigate the membership problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge