Learning 3-Manifold Triangulations

Real 3-manifold triangulations can be uniquely represented by isomorphism signatures. Databases of these isomorphism signatures are generated for a variety of 3-manifolds and knot complements, using SnapPy and Regina, then these language-like inputs are used to train various machine learning architectures to differentiate the manifolds, as well as their Dehn surgeries, via their triangulations. Gradient saliency analysis then extracts key parts of this language-like encoding scheme from the trained models. The isomorphism signature databases are taken from the 3-manifolds' Pachner graphs, which are also generated in bulk for some selected manifolds of focus and for the subset of the SnapPy orientable cusped census with $<8$ initial tetrahedra. These Pachner graphs are further analysed through the lens of network science to identify new structure in the triangulation representation; in particular for the hyperbolic case, a relation between the length of the shortest geodesic (systole) and the size of the Pachner graph's ball is observed.

Machine Learning Clifford invariants of ADE Coxeter elements

There has been recent interest in novel Clifford geometric invariants of linear transformations. This motivates the investigation of such invariants for a certain type of geometric transformation of interest in the context of root systems, reflection groups, Lie groups and Lie algebras: the Coxeter transformations. We perform exhaustive calculations of all Coxeter transformations for $A_8$, $D_8$ and $E_8$ for a choice of basis of simple roots and compute their invariants, using high-performance computing. This computational algebra paradigm generates a dataset that can then be mined using techniques from data science such as supervised and unsupervised machine learning. In this paper we focus on neural network classification and principal component analysis. Since the output -- the invariants -- is fully determined by the choice of simple roots and the permutation order of the corresponding reflections in the Coxeter element, we expect huge degeneracy in the mapping. This provides the perfect setup for machine learning, and indeed we see that the datasets can be machine learned to very high accuracy. This paper is a pump-priming study in experimental mathematics using Clifford algebras, showing that such Clifford algebraic datasets are amenable to machine learning, and shedding light on relationships between these novel and other well-known geometric invariants and also giving rise to analytic results.

Machine Learning Algebraic Geometry for Physics

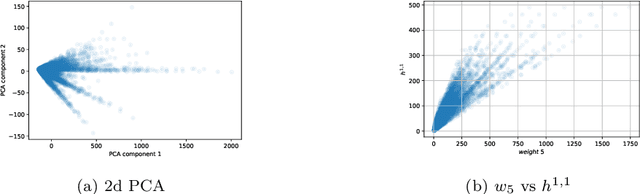
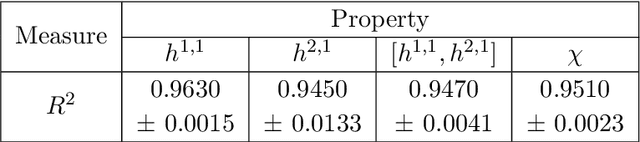
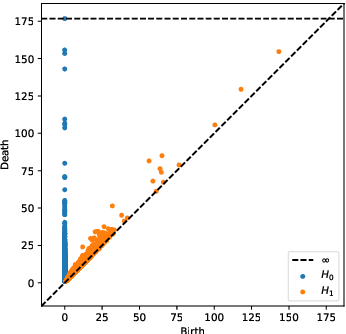
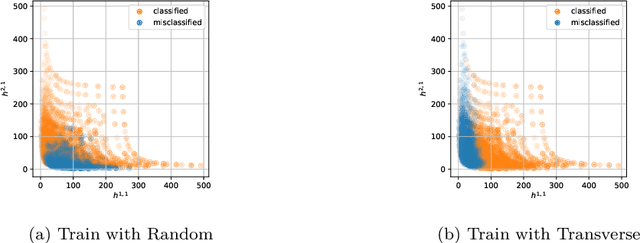
We review some recent applications of machine learning to algebraic geometry and physics. Since problems in algebraic geometry can typically be reformulated as mappings between tensors, this makes them particularly amenable to supervised learning. Additionally, unsupervised methods can provide insight into the structure of such geometrical data. At the heart of this programme is the question of how geometry can be machine learned, and indeed how AI helps one to do mathematics. This is a chapter contribution to the book Machine learning and Algebraic Geometry, edited by A. Kasprzyk et al.

Cluster Algebras: Network Science and Machine Learning

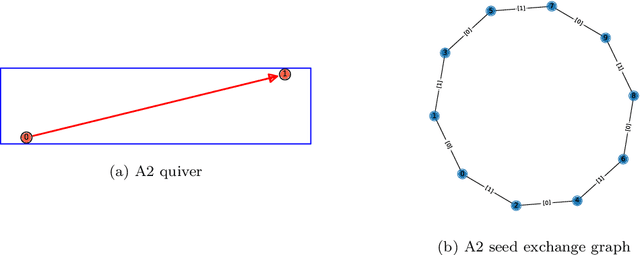
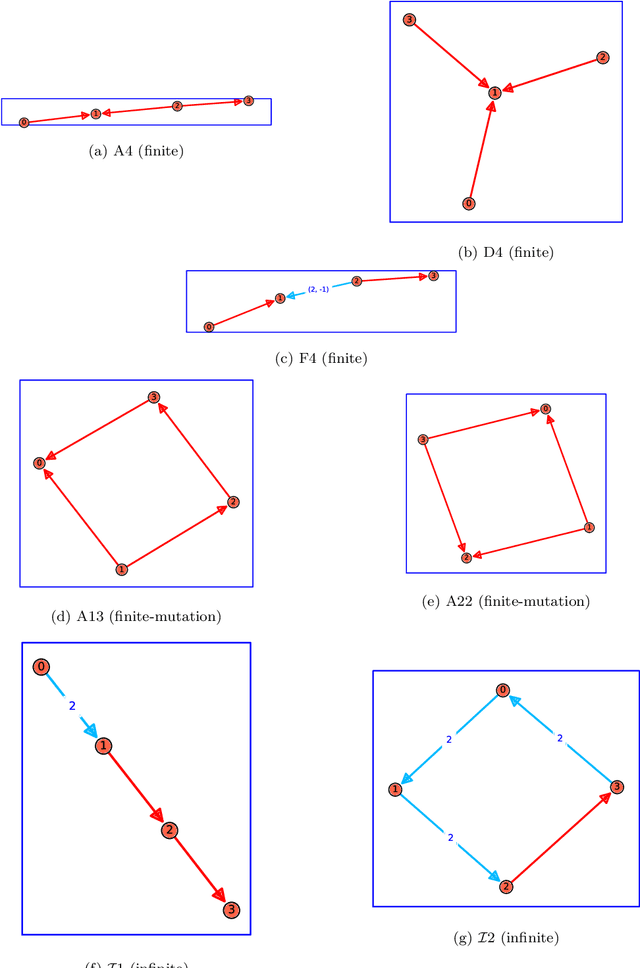
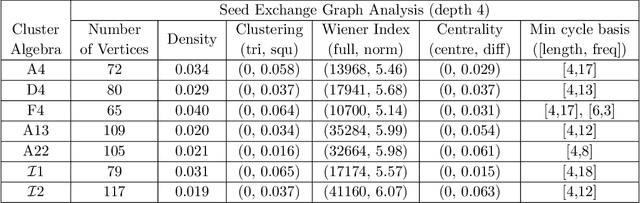
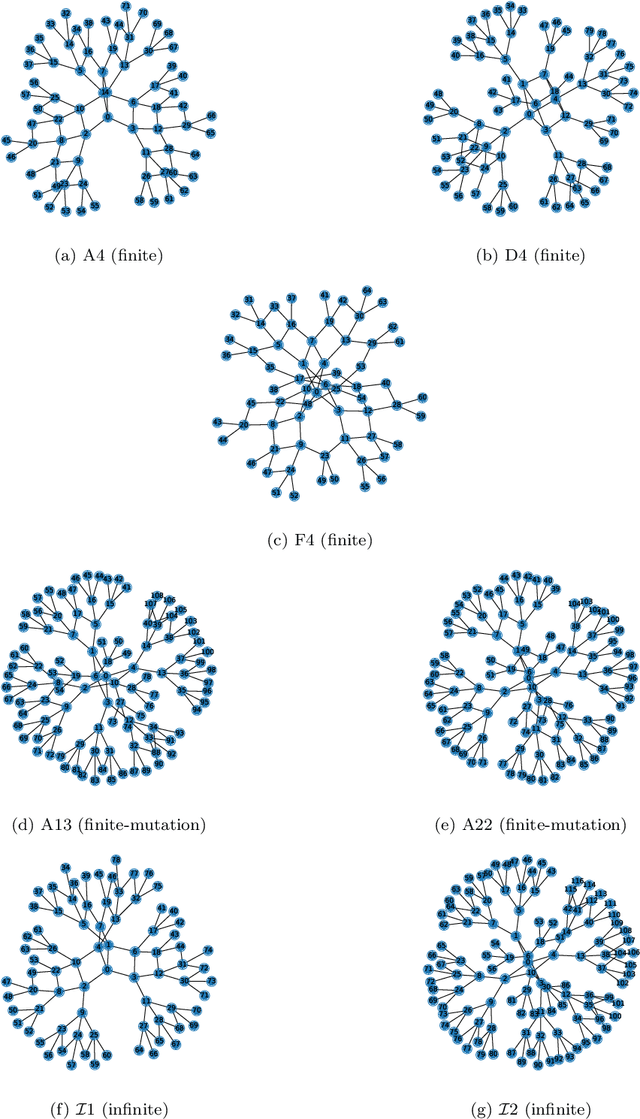
Cluster algebras have recently become an important player in mathematics and physics. In this work, we investigate them through the lens of modern data science, specifically with techniques from network science and machine-learning. Network analysis methods are applied to the exchange graphs for cluster algebras of varying mutation types. The analysis indicates that when the graphs are represented without identifying by permutation equivalence between clusters an elegant symmetry emerges in the quiver exchange graph embedding. The ratio between number of seeds and number of quivers associated to this symmetry is computed for finite Dynkin type algebras up to rank 5, and conjectured for higher ranks. Simple machine learning techniques successfully learn to differentiate cluster algebras from their seeds. The learning performance exceeds 0.9 accuracies between algebras of the same mutation type and between types, as well as relative to artificially generated data.