Edward Hirst
Grokking vs. Learning: Same Features, Different Encodings
Feb 03, 2025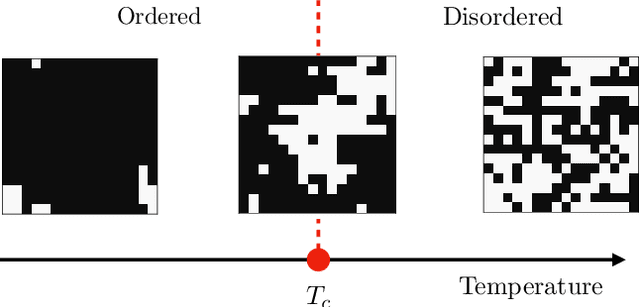
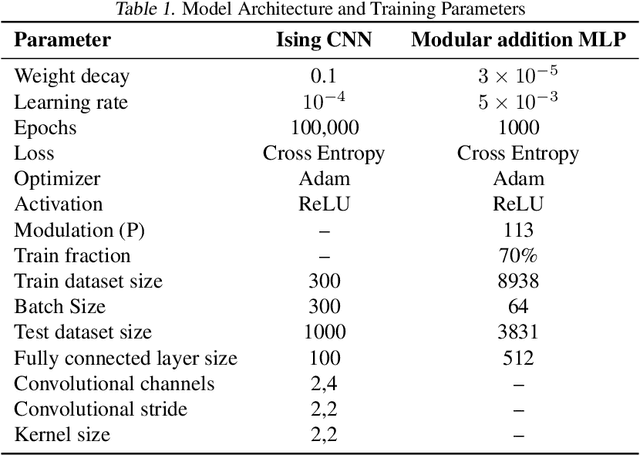
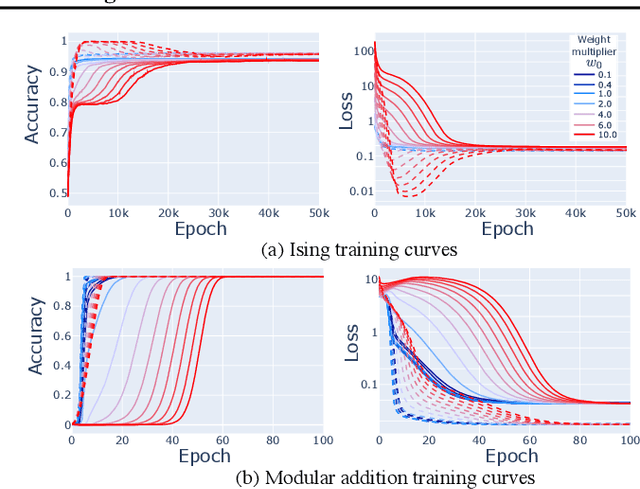
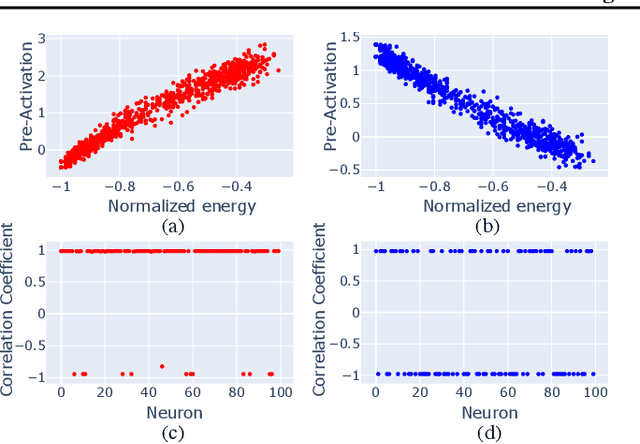
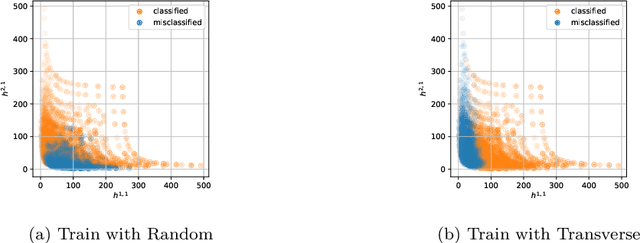
Abstract:Grokking typically achieves similar loss to ordinary, "steady", learning. We ask whether these different learning paths - grokking versus ordinary training - lead to fundamental differences in the learned models. To do so we compare the features, compressibility, and learning dynamics of models trained via each path in two tasks. We find that grokked and steadily trained models learn the same features, but there can be large differences in the efficiency with which these features are encoded. In particular, we find a novel "compressive regime" of steady training in which there emerges a linear trade-off between model loss and compressibility, and which is absent in grokking. In this regime, we can achieve compression factors 25x times the base model, and 5x times the compression achieved in grokking. We then track how model features and compressibility develop through training. We show that model development in grokking is task-dependent, and that peak compressibility is achieved immediately after the grokking plateau. Finally, novel information-geometric measures are introduced which demonstrate that models undergoing grokking follow a straight path in information space.
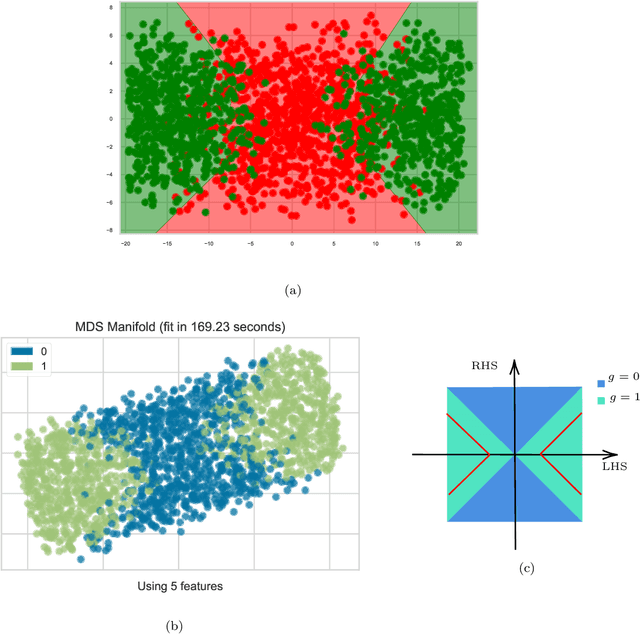
Machine Learning Mutation-Acyclicity of Quivers
Nov 06, 2024


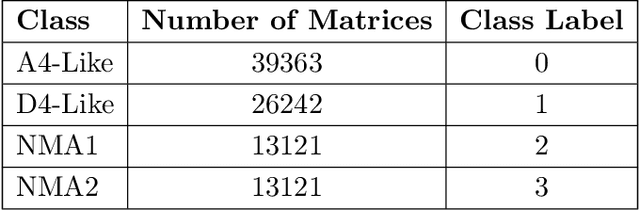
Abstract:Machine learning (ML) has emerged as a powerful tool in mathematical research in recent years. This paper applies ML techniques to the study of quivers--a type of directed multigraph with significant relevance in algebra, combinatorics, computer science, and mathematical physics. Specifically, we focus on the challenging problem of determining the mutation-acyclicity of a quiver on 4 vertices, a property that is pivotal since mutation-acyclicity is often a necessary condition for theorems involving path algebras and cluster algebras. Although this classification is known for quivers with at most 3 vertices, little is known about quivers on more than 3 vertices. We give a computer-assisted proof of a theorem to prove that mutation-acyclicity is decidable for quivers on 4 vertices with edge weight at most 2. By leveraging neural networks (NNs) and support vector machines (SVMs), we then accurately classify more general 4-vertex quivers as mutation-acyclic or non-mutation-acyclic. Our results demonstrate that ML models can efficiently detect mutation-acyclicity, providing a promising computational approach to this combinatorial problem, from which the trained SVM equation provides a starting point to guide future theoretical development.
Learning 3-Manifold Triangulations
May 15, 2024Abstract:Real 3-manifold triangulations can be uniquely represented by isomorphism signatures. Databases of these isomorphism signatures are generated for a variety of 3-manifolds and knot complements, using SnapPy and Regina, then these language-like inputs are used to train various machine learning architectures to differentiate the manifolds, as well as their Dehn surgeries, via their triangulations. Gradient saliency analysis then extracts key parts of this language-like encoding scheme from the trained models. The isomorphism signature databases are taken from the 3-manifolds' Pachner graphs, which are also generated in bulk for some selected manifolds of focus and for the subset of the SnapPy orientable cusped census with $<8$ initial tetrahedra. These Pachner graphs are further analysed through the lens of network science to identify new structure in the triangulation representation; in particular for the hyperbolic case, a relation between the length of the shortest geodesic (systole) and the size of the Pachner graph's ball is observed.
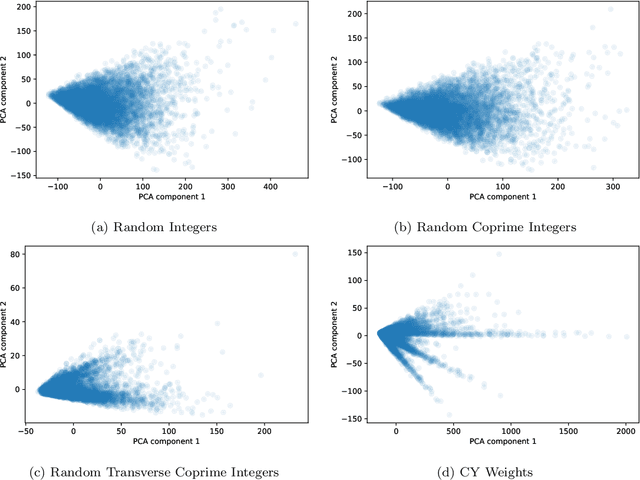
Calabi-Yau Four/Five/Six-folds as $\mathbb{P}^n_\textbf{w}$ Hypersurfaces: Machine Learning, Approximation, and Generation
Nov 28, 2023



Abstract:Calabi-Yau four-folds may be constructed as hypersurfaces in weighted projective spaces of complex dimension 5 defined via weight systems of 6 weights. In this work, neural networks were implemented to learn the Calabi-Yau Hodge numbers from the weight systems, where gradient saliency and symbolic regression then inspired a truncation of the Landau-Ginzburg model formula for the Hodge numbers of any dimensional Calabi-Yau constructed in this way. The approximation always provides a tight lower bound, is shown to be dramatically quicker to compute (with compute times reduced by up to four orders of magnitude), and gives remarkably accurate results for systems with large weights. Additionally, complementary datasets of weight systems satisfying the necessary but insufficient conditions for transversality were constructed, including considerations of the IP, reflexivity, and intradivisibility properties. Overall producing a classification of this weight system landscape, further confirmed with machine learning methods. Using the knowledge of this classification, and the properties of the presented approximation, a novel dataset of transverse weight systems consisting of 7 weights was generated for a sum of weights $\leq 200$; producing a new database of Calabi-Yau five-folds, with their respective topological properties computed. Further to this an equivalent database of candidate Calabi-Yau six-folds was generated with approximated Hodge numbers.
Machine Learning Clifford invariants of ADE Coxeter elements
Sep 29, 2023Abstract:There has been recent interest in novel Clifford geometric invariants of linear transformations. This motivates the investigation of such invariants for a certain type of geometric transformation of interest in the context of root systems, reflection groups, Lie groups and Lie algebras: the Coxeter transformations. We perform exhaustive calculations of all Coxeter transformations for $A_8$, $D_8$ and $E_8$ for a choice of basis of simple roots and compute their invariants, using high-performance computing. This computational algebra paradigm generates a dataset that can then be mined using techniques from data science such as supervised and unsupervised machine learning. In this paper we focus on neural network classification and principal component analysis. Since the output -- the invariants -- is fully determined by the choice of simple roots and the permutation order of the corresponding reflections in the Coxeter element, we expect huge degeneracy in the mapping. This provides the perfect setup for machine learning, and indeed we see that the datasets can be machine learned to very high accuracy. This paper is a pump-priming study in experimental mathematics using Clifford algebras, showing that such Clifford algebraic datasets are amenable to machine learning, and shedding light on relationships between these novel and other well-known geometric invariants and also giving rise to analytic results.
Machine Learning Algebraic Geometry for Physics
Apr 21, 2022
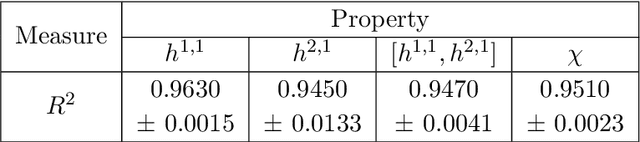
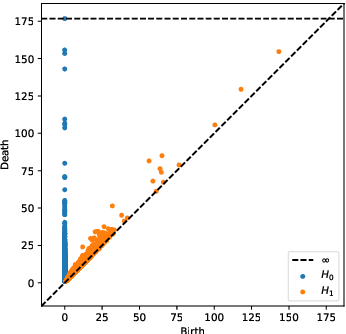
Abstract:We review some recent applications of machine learning to algebraic geometry and physics. Since problems in algebraic geometry can typically be reformulated as mappings between tensors, this makes them particularly amenable to supervised learning. Additionally, unsupervised methods can provide insight into the structure of such geometrical data. At the heart of this programme is the question of how geometry can be machine learned, and indeed how AI helps one to do mathematics. This is a chapter contribution to the book Machine learning and Algebraic Geometry, edited by A. Kasprzyk et al.
Cluster Algebras: Network Science and Machine Learning
Mar 25, 2022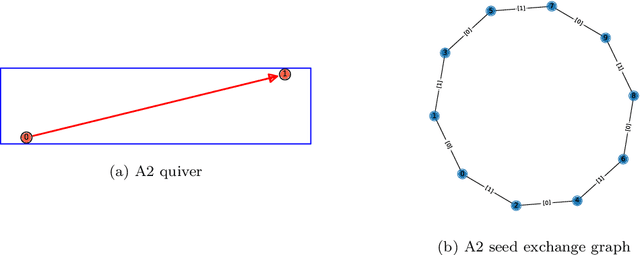
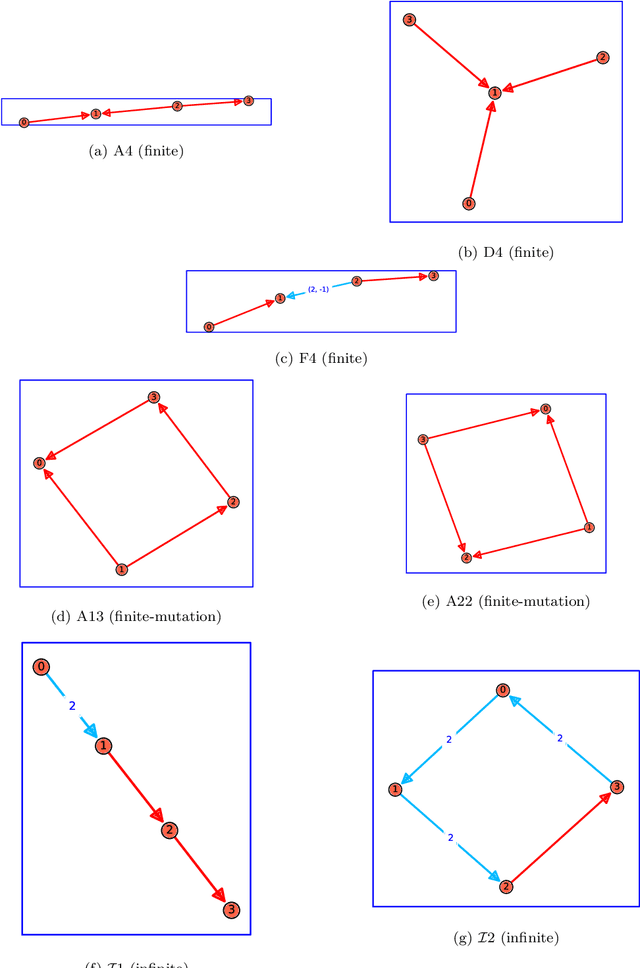
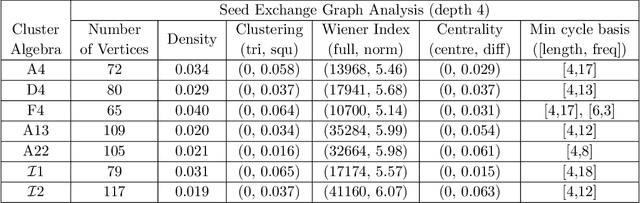
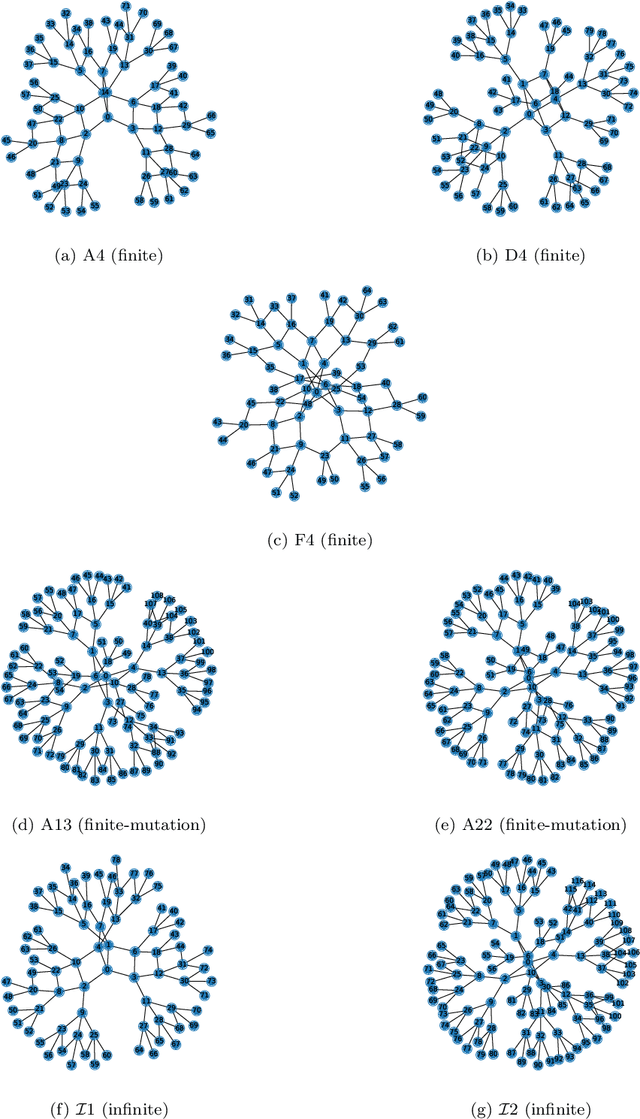
Abstract:Cluster algebras have recently become an important player in mathematics and physics. In this work, we investigate them through the lens of modern data science, specifically with techniques from network science and machine-learning. Network analysis methods are applied to the exchange graphs for cluster algebras of varying mutation types. The analysis indicates that when the graphs are represented without identifying by permutation equivalence between clusters an elegant symmetry emerges in the quiver exchange graph embedding. The ratio between number of seeds and number of quivers associated to this symmetry is computed for finite Dynkin type algebras up to rank 5, and conjectured for higher ranks. Simple machine learning techniques successfully learn to differentiate cluster algebras from their seeds. The learning performance exceeds 0.9 accuracies between algebras of the same mutation type and between types, as well as relative to artificially generated data.
Machine Learning Calabi-Yau Hypersurfaces
Dec 12, 2021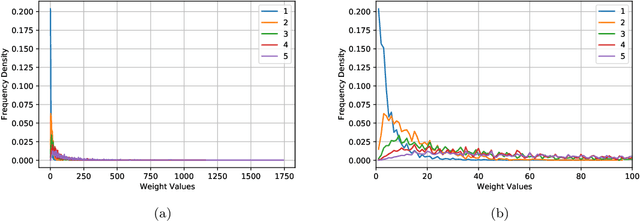
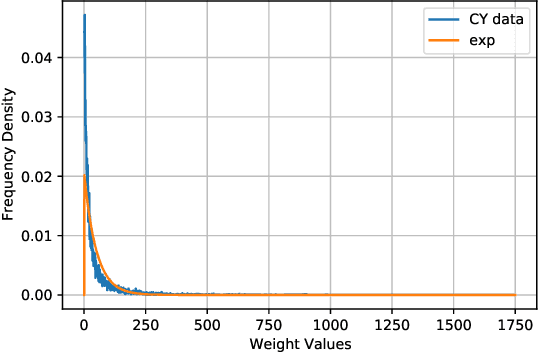
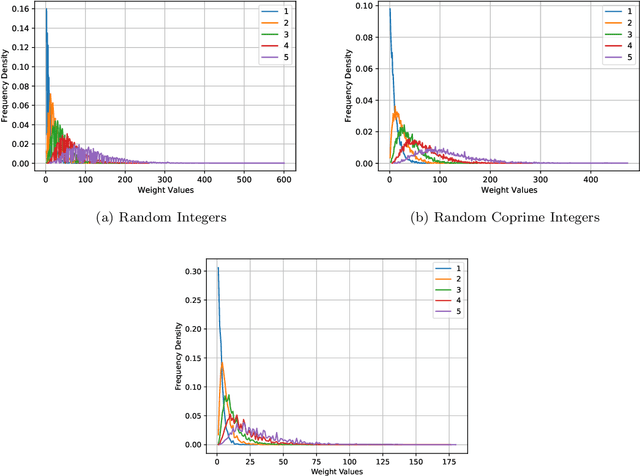
Abstract:We revisit the classic database of weighted-P4s which admit Calabi-Yau 3-fold hypersurfaces equipped with a diverse set of tools from the machine-learning toolbox. Unsupervised techniques identify an unanticipated almost linear dependence of the topological data on the weights. This then allows us to identify a previously unnoticed clustering in the Calabi-Yau data. Supervised techniques are successful in predicting the topological parameters of the hypersurface from its weights with an accuracy of R^2 > 95%. Supervised learning also allows us to identify weighted-P4s which admit Calabi-Yau hypersurfaces to 100% accuracy by making use of partitioning supported by the clustering behaviour.
Neurons on Amoebae
Jun 07, 2021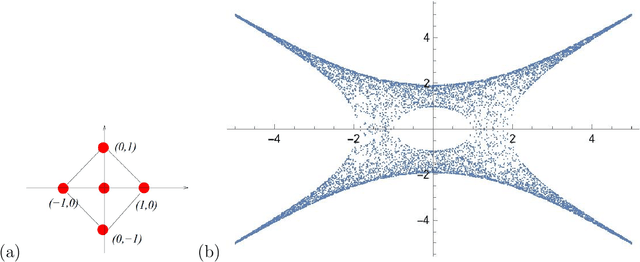


Abstract:We apply methods of machine-learning, such as neural networks, manifold learning and image processing, in order to study amoebae in algebraic geometry and string theory. With the help of embedding manifold projection, we recover complicated conditions obtained from so-called lopsidedness. For certain cases (e.g. lopsided amoeba with positive coefficients for $F_0$), it could even reach $\sim99\%$ accuracy. Using weights and biases, we also find good approximations to determine the genus for an amoeba at lower computational cost. In general, the models could easily predict the genus with over $90\%$ accuracies. With similar techniques, we also investigate the membership problem.
Machine-Learning Dessins d'Enfants: Explorations via Modular and Seiberg-Witten Curves
Apr 22, 2020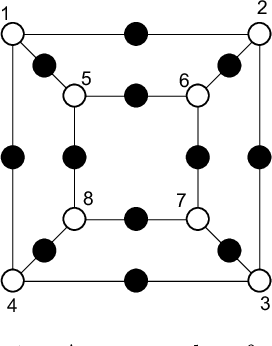


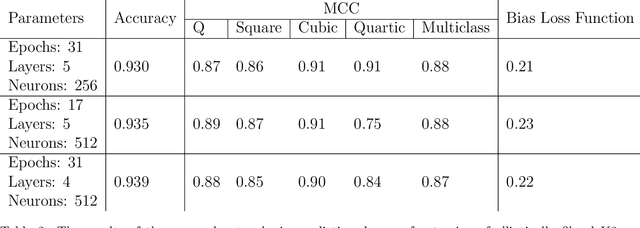
Abstract:We apply machine-learning to the study of dessins d'enfants. Specifically, we investigate a class of dessins which reside at the intersection of the investigations of modular subgroups, Seiberg-Witten curves and extremal elliptic K3 surfaces. A deep feed-forward neural network with simple structure and standard activation functions without prior knowledge of the underlying mathematics is established and imposed onto the classification of extension degree over the rationals, known to be a difficult problem. The classifications exceeded 0.93 accuracy and around 0.9 confidence relatively quickly. The Seiberg-Witten curves for those with rational coefficients are also tabulated.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge