David S. Berman
A path to natural language through tokenisation and transformers
Jan 06, 2026Abstract:Natural languages exhibit striking regularities in their statistical structure, including notably the emergence of Zipf's and Heaps' laws. Despite this, it remains broadly unclear how these properties relate to the modern tokenisation schemes used in contemporary transformer models. In this note, we analyse the information content (as measured by the Shannon entropy) of various corpora under the assumption of a Zipfian frequency distribution, and derive a closed-form expression for the slot entropy expectation value. We then empirically investigate how byte--pair encoding (BPE) transforms corpus statistics, showing that recursive applications of BPE drive token frequencies toward a Zipfian power law while inducing a characteristic growth pattern in empirical entropy. Utilizing the ability of transformers to learn context dependent token probability distributions, we train language models on corpora tokenised at varying BPE depths, revealing that the model predictive entropies increasingly agree with Zipf-derived predictions as the BPE depth increases. Attention-based diagnostics further indicate that deeper tokenisation reduces local token dependencies, bringing the empirical distribution closer to the weakly dependent (near IID) regime. Together, these results clarify how BPE acts not only as a compression mechanism but also as a statistical transform that reconstructs key informational properties of natural language.
Grokking vs. Learning: Same Features, Different Encodings
Feb 03, 2025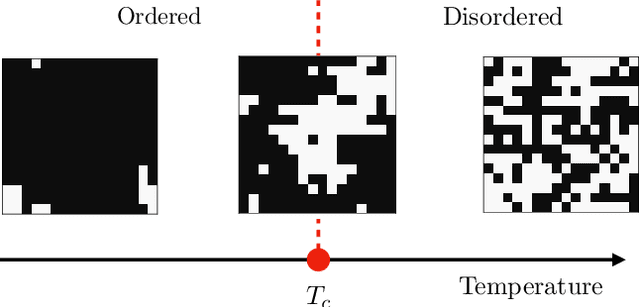
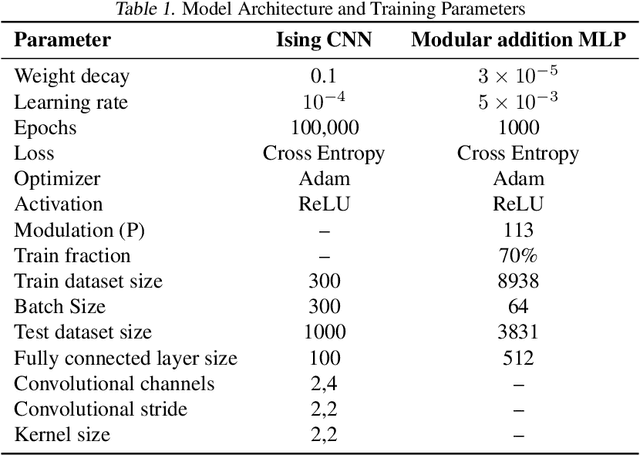
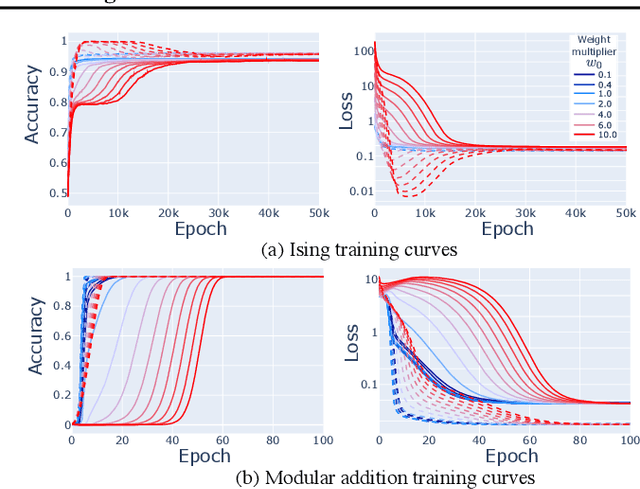
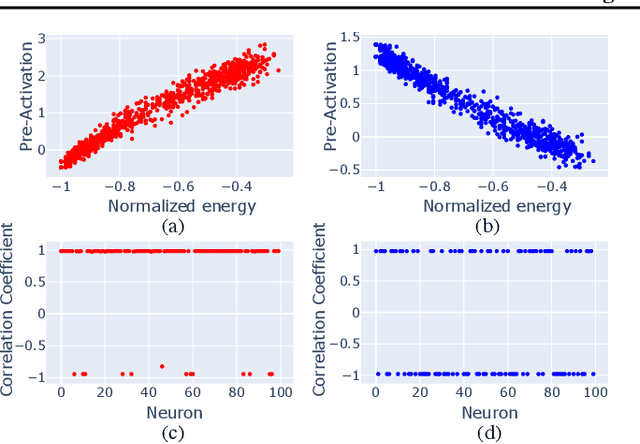
Abstract:Grokking typically achieves similar loss to ordinary, "steady", learning. We ask whether these different learning paths - grokking versus ordinary training - lead to fundamental differences in the learned models. To do so we compare the features, compressibility, and learning dynamics of models trained via each path in two tasks. We find that grokked and steadily trained models learn the same features, but there can be large differences in the efficiency with which these features are encoded. In particular, we find a novel "compressive regime" of steady training in which there emerges a linear trade-off between model loss and compressibility, and which is absent in grokking. In this regime, we can achieve compression factors 25x times the base model, and 5x times the compression achieved in grokking. We then track how model features and compressibility develop through training. We show that model development in grokking is task-dependent, and that peak compressibility is achieved immediately after the grokking plateau. Finally, novel information-geometric measures are introduced which demonstrate that models undergoing grokking follow a straight path in information space.
NCoder -- A Quantum Field Theory approach to encoding data
Feb 01, 2024Abstract:In this paper we present a novel approach to interpretable AI inspired by Quantum Field Theory (QFT) which we call the NCoder. The NCoder is a modified autoencoder neural network whose latent layer is prescribed to be a subset of $n$-point correlation functions. Regarding images as draws from a lattice field theory, this architecture mimics the task of perturbatively constructing the effective action of the theory order by order in an expansion using Feynman diagrams. Alternatively, the NCoder may be regarded as simulating the procedure of statistical inference whereby high dimensional data is first summarized in terms of several lower dimensional summary statistics (here the $n$-point correlation functions), and subsequent out-of-sample data is generated by inferring the data generating distribution from these statistics. In this way the NCoder suggests a fascinating correspondence between perturbative renormalizability and the sufficiency of models. We demonstrate the efficacy of the NCoder by applying it to the generation of MNIST images, and find that generated images can be correctly classified using only information from the first three $n$-point functions of the image distribution.
Bayesian Renormalization
May 17, 2023Abstract:In this note we present a fully information theoretic approach to renormalization inspired by Bayesian statistical inference, which we refer to as Bayesian Renormalization. The main insight of Bayesian Renormalization is that the Fisher metric defines a correlation length that plays the role of an emergent RG scale quantifying the distinguishability between nearby points in the space of probability distributions. This RG scale can be interpreted as a proxy for the maximum number of unique observations that can be made about a given system during a statistical inference experiment. The role of the Bayesian Renormalization scheme is subsequently to prepare an effective model for a given system up to a precision which is bounded by the aforementioned scale. In applications of Bayesian Renormalization to physical systems, the emergent information theoretic scale is naturally identified with the maximum energy that can be probed by current experimental apparatus, and thus Bayesian Renormalization coincides with ordinary renormalization. However, Bayesian Renormalization is sufficiently general to apply even in circumstances in which an immediate physical scale is absent, and thus provides an ideal approach to renormalization in data science contexts. To this end, we provide insight into how the Bayesian Renormalization scheme relates to existing methods for data compression and data generation such as the information bottleneck and the diffusion learning paradigm.
On the Dynamics of Inference and Learning
Apr 19, 2022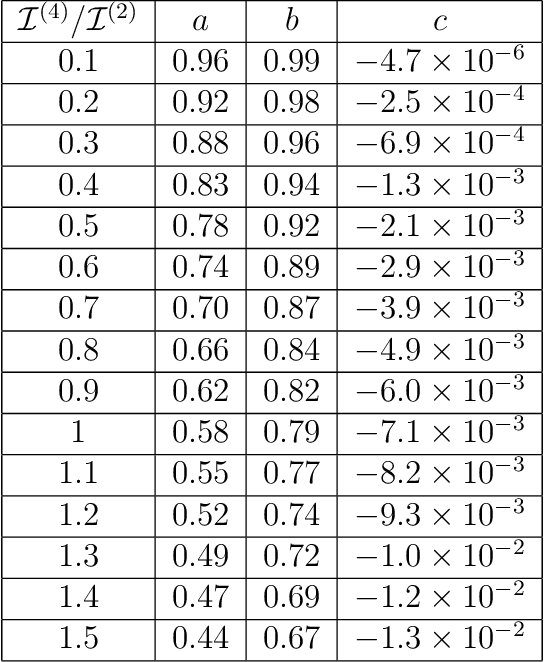


Abstract:Statistical Inference is the process of determining a probability distribution over the space of parameters of a model given a data set. As more data becomes available this probability distribution becomes updated via the application of Bayes' theorem. We present a treatment of this Bayesian updating process as a continuous dynamical system. Statistical inference is then governed by a first order differential equation describing a trajectory or flow in the information geometry determined by a parametric family of models. We solve this equation for some simple models and show that when the Cram\'{e}r-Rao bound is saturated the learning rate is governed by a simple $1/T$ power-law, with $T$ a time-like variable denoting the quantity of data. The presence of hidden variables can be incorporated in this setting, leading to an additional driving term in the resulting flow equation. We illustrate this with both analytic and numerical examples based on Gaussians and Gaussian Random Processes and inference of the coupling constant in the 1D Ising model. Finally we compare the qualitative behaviour exhibited by Bayesian flows to the training of various neural networks on benchmarked data sets such as MNIST and CIFAR10 and show how that for networks exhibiting small final losses the simple power-law is also satisfied.
Machine Learning Calabi-Yau Hypersurfaces
Dec 12, 2021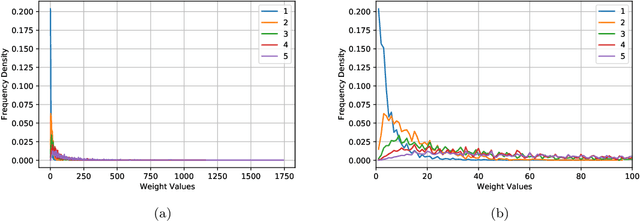
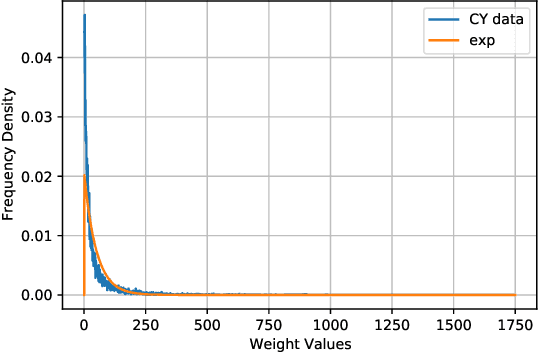
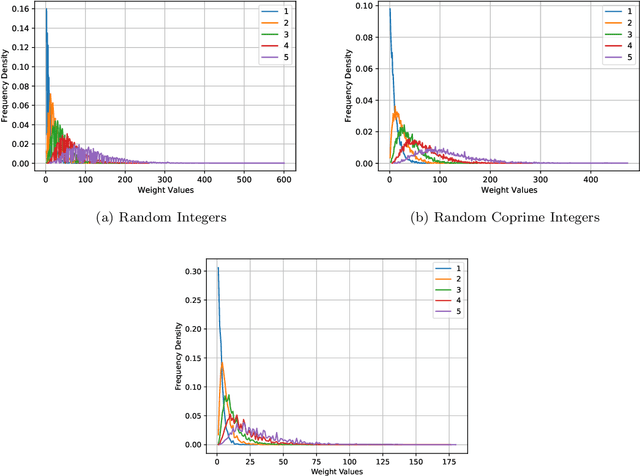
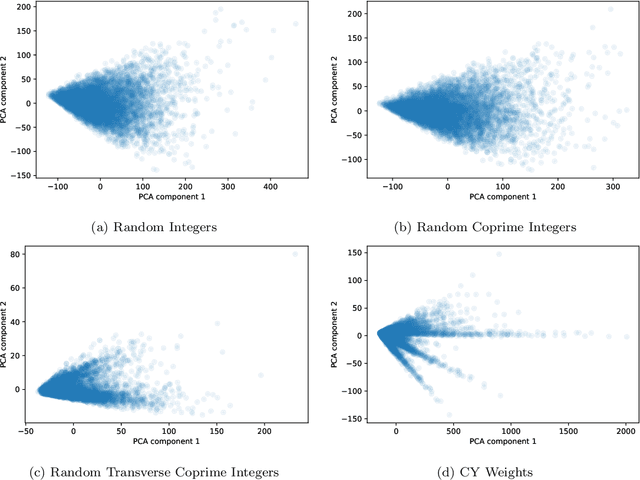
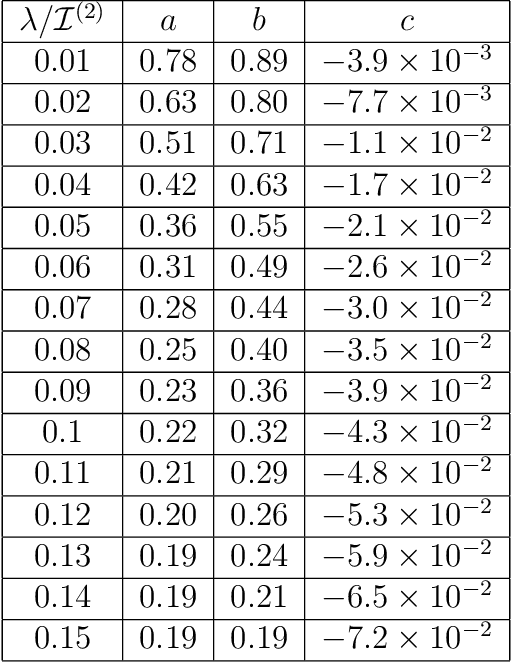
Abstract:We revisit the classic database of weighted-P4s which admit Calabi-Yau 3-fold hypersurfaces equipped with a diverse set of tools from the machine-learning toolbox. Unsupervised techniques identify an unanticipated almost linear dependence of the topological data on the weights. This then allows us to identify a previously unnoticed clustering in the Calabi-Yau data. Supervised techniques are successful in predicting the topological parameters of the hypersurface from its weights with an accuracy of R^2 > 95%. Supervised learning also allows us to identify weighted-P4s which admit Calabi-Yau hypersurfaces to 100% accuracy by making use of partitioning supported by the clustering behaviour.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge