Multi-Camera Visual-Inertial Simultaneous Localization and Mapping for Autonomous Valet Parking

Localization and mapping are key capabilities for self-driving vehicles. This paper describes a visual-inertial SLAM system that estimates an accurate and globally consistent trajectory of the vehicle and reconstructs a dense model of the free space surrounding the car. Towards this goal, we build on Kimera and extend it to use multiple cameras as well as external (e.g. wheel) odometry sensors, to obtain accurate and robust odometry estimates in real-world problems. Additionally, we propose an effective scheme for closing loops that circumvents the drawbacks of common alternatives based on the Perspective-n-Point method and also works with a single monocular camera. Finally, we develop a method for dense 3D mapping of the free space that combines a segmentation network for free-space detection with a homography-based dense mapping technique. We test our system on photo-realistic simulations and on several real datasets collected by a car prototype developed by the Ford Motor Company, spanning both indoor and outdoor parking scenarios. Our multi-camera system is shown to outperform state-of-the art open-source visual-inertial-SLAM pipelines (Vins-Fusion, ORB-SLAM3), and exhibits an average trajectory error under 1% of the trajectory length across more than 8 km of distance traveled (combined across all datasets). A video showcasing the system is available here: youtu.be/H8CpzDpXOI8

On the Dynamics of Inference and Learning

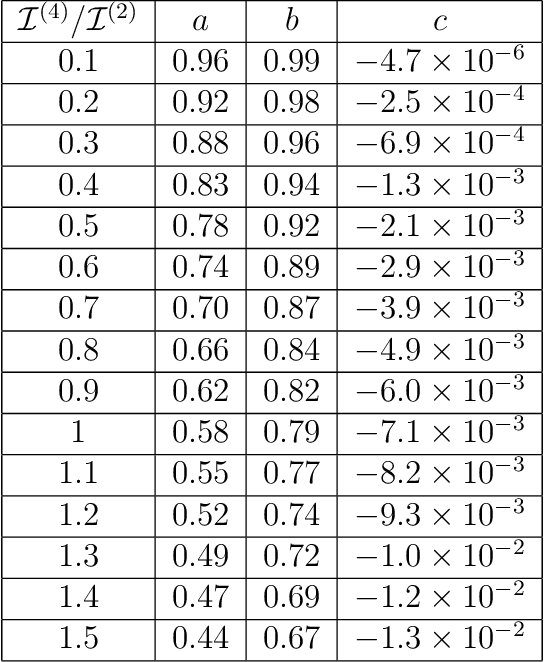
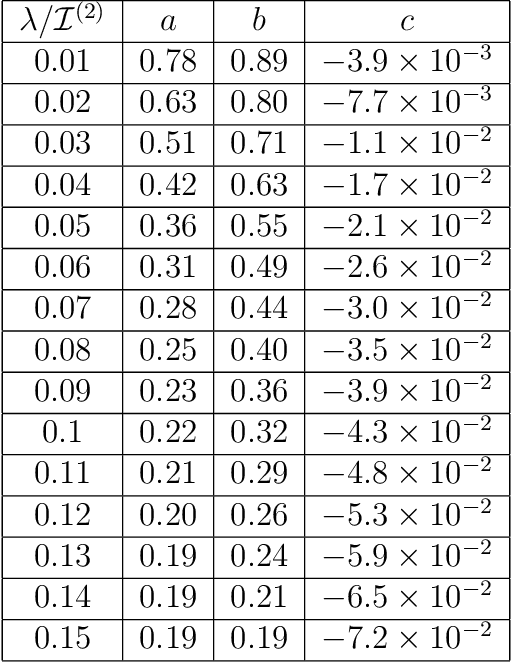
Statistical Inference is the process of determining a probability distribution over the space of parameters of a model given a data set. As more data becomes available this probability distribution becomes updated via the application of Bayes' theorem. We present a treatment of this Bayesian updating process as a continuous dynamical system. Statistical inference is then governed by a first order differential equation describing a trajectory or flow in the information geometry determined by a parametric family of models. We solve this equation for some simple models and show that when the Cram\'{e}r-Rao bound is saturated the learning rate is governed by a simple $1/T$ power-law, with $T$ a time-like variable denoting the quantity of data. The presence of hidden variables can be incorporated in this setting, leading to an additional driving term in the resulting flow equation. We illustrate this with both analytic and numerical examples based on Gaussians and Gaussian Random Processes and inference of the coupling constant in the 1D Ising model. Finally we compare the qualitative behaviour exhibited by Bayesian flows to the training of various neural networks on benchmarked data sets such as MNIST and CIFAR10 and show how that for networks exhibiting small final losses the simple power-law is also satisfied.