Finding Clustering Algorithms in the Transformer Architecture

The invention of the transformer architecture has revolutionized Artificial Intelligence (AI), yielding unprecedented success in areas such as natural language processing, computer vision, and multimodal reasoning. Despite these advances, it is unclear whether transformers are able to learn and implement precise algorithms. Here, we demonstrate that transformers can exactly implement a fundamental and widely used algorithm for $k$-means clustering: Lloyd's algorithm. First, we theoretically prove the existence of such a transformer architecture, which we term the $k$-means transformer, that exactly implements Lloyd's algorithm for $k$-means clustering using the standard ingredients of modern transformers: attention and residual connections. Next, we numerically implement this transformer and demonstrate in experiments the exact correspondence between our architecture and Lloyd's algorithm, providing a fully neural implementation of $k$-means clustering. Finally, we demonstrate that interpretable alterations (e.g., incorporating layer normalizations or multilayer perceptrons) to this architecture yields diverse and novel variants of clustering algorithms, such as soft $k$-means, spherical $k$-means, trimmed $k$-means, and more. Collectively, our findings demonstrate how transformer mechanisms can precisely map onto algorithmic procedures, offering a clear and interpretable perspective on implementing precise algorithms in transformers.

Transformers Learn Faster with Semantic Focus

Various forms of sparse attention have been explored to mitigate the quadratic computational and memory cost of the attention mechanism in transformers. We study sparse transformers not through a lens of efficiency but rather in terms of learnability and generalization. Empirically studying a range of attention mechanisms, we find that input-dependent sparse attention models appear to converge faster and generalize better than standard attention models, while input-agnostic sparse attention models show no such benefits -- a phenomenon that is robust across architectural and optimization hyperparameter choices. This can be interpreted as demonstrating that concentrating a model's "semantic focus" with respect to the tokens currently being considered (in the form of input-dependent sparse attention) accelerates learning. We develop a theoretical characterization of the conditions that explain this behavior. We establish a connection between the stability of the standard softmax and the loss function's Lipschitz properties, then show how sparsity affects the stability of the softmax and the subsequent convergence and generalization guarantees resulting from the attention mechanism. This allows us to theoretically establish that input-agnostic sparse attention does not provide any benefits. We also characterize conditions when semantic focus (input-dependent sparse attention) can provide improved guarantees, and we validate that these conditions are in fact met in our empirical evaluations.

Capacity Analysis of Vector Symbolic Architectures

Hyperdimensional computing (HDC) is a biologically-inspired framework that uses high-dimensional vectors and various vector operations to represent and manipulate symbols. The ensemble of a particular vector space and two vector operations (one addition-like for "bundling" and one outer-product-like for "binding") form what is called a "vector symbolic architecture" (VSA). While VSAs have been employed in numerous applications and studied empirically, many theoretical questions about VSAs remain open. We provide theoretical analyses for the *representation capacities* of three popular VSAs: MAP-I, MAP-B, and Binary Sparse. Representation capacity here refers to upper bounds on the dimensions of the VSA vectors required to perform certain symbolic tasks (such as testing for set membership $i \in S$ and estimating set intersection sizes $|S \cap T|$) to a given degree of accuracy. We also describe a relationship between the MAP-I VSA to Hopfield networks, which are simple models of associative memory, and analyze the ability of Hopfield networks to perform some of the same tasks that are typically asked of VSAs. Our analysis of MAP-I casts the VSA vectors as the outputs of *sketching* (dimensionality reduction) algorithms such as the Johnson-Lindenstrauss transform; this provides a clean, simple framework for obtaining bounds on MAP-I's representation capacity. We also provide, to our knowledge, the first analysis of testing set membership in a bundle of general pairwise bindings from MAP-I. Binary sparse VSAs are well-known to be related to Bloom filters; we give analyses of set intersection for Bloom and Counting Bloom filters. Our analysis of MAP-B and Binary Sparse bundling include new applications of several concentration inequalities.

Bayesian Experimental Design for Symbolic Discovery

This study concerns the formulation and application of Bayesian optimal experimental design to symbolic discovery, which is the inference from observational data of predictive models taking general functional forms. We apply constrained first-order methods to optimize an appropriate selection criterion, using Hamiltonian Monte Carlo to sample from the prior. A step for computing the predictive distribution, involving convolution, is computed via either numerical integration, or via fast transform methods.

Towards Quantum Advantage on Noisy Quantum Computers

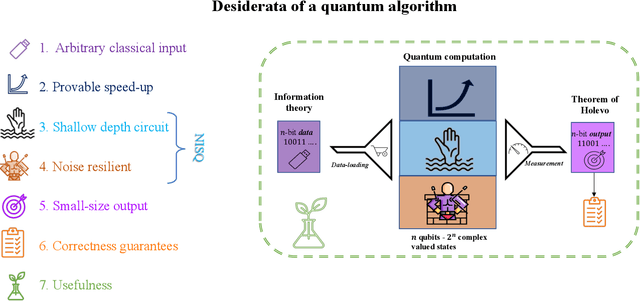
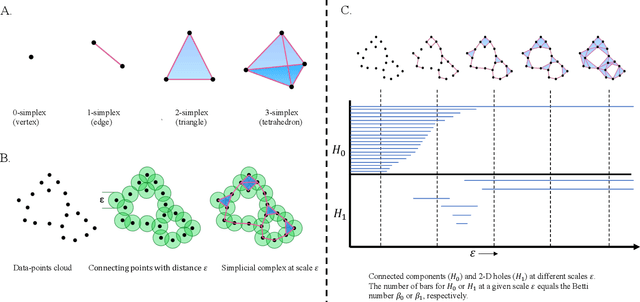
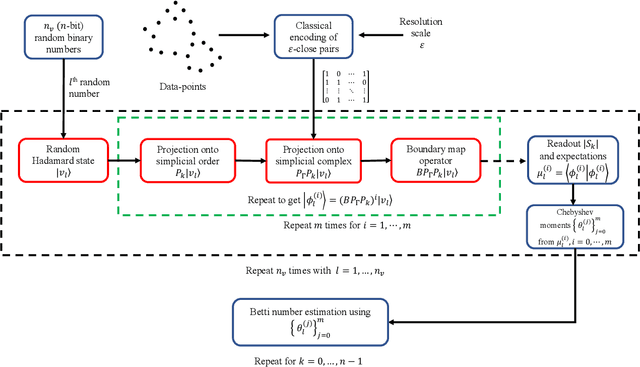
Topological data analysis (TDA) is a powerful technique for extracting complex and valuable shape-related summaries of high-dimensional data. However, the computational demands of classical TDA algorithms are exorbitant, and quickly become impractical for high-order characteristics. Quantum computing promises exponential speedup for certain problems. Yet, many existing quantum algorithms with notable asymptotic speedups require a degree of fault tolerance that is currently unavailable. In this paper, we present NISQ-TDA, the first fully implemented end-to-end quantum machine learning algorithm needing only a linear circuit-depth, that is applicable to non-handcrafted high-dimensional classical data, with potential speedup under stringent conditions. The algorithm neither suffers from the data-loading problem nor does it need to store the input data on the quantum computer explicitly. Our approach includes three key innovations: (a) an efficient realization of the full boundary operator as a sum of Pauli operators; (b) a quantum rejection sampling and projection approach to restrict a uniform superposition to the simplices of the desired order in the complex; and (c) a stochastic rank estimation method to estimate the topological features in the form of approximate Betti numbers. We present theoretical results that establish additive error guarantees for NISQ-TDA, and the circuit and computational time and depth complexities for exponentially scaled output estimates, up to the error tolerance. The algorithm was successfully executed on quantum computing devices, as well as on noisy quantum simulators, applied to small datasets. Preliminary empirical results suggest that the algorithm is robust to noise.

Low-Rank Approximation with $1/ε^{1/3}$ Matrix-Vector Products

We study iterative methods based on Krylov subspaces for low-rank approximation under any Schatten-$p$ norm. Here, given access to a matrix $A$ through matrix-vector products, an accuracy parameter $\epsilon$, and a target rank $k$, the goal is to find a rank-$k$ matrix $Z$ with orthonormal columns such that $\| A(I -ZZ^\top)\|_{S_p} \leq (1+\epsilon)\min_{U^\top U = I_k} \|A(I - U U^\top)\|_{S_p}$, where $\|M\|_{S_p}$ denotes the $\ell_p$ norm of the the singular values of $M$. For the special cases of $p=2$ (Frobenius norm) and $p = \infty$ (Spectral norm), Musco and Musco (NeurIPS 2015) obtained an algorithm based on Krylov methods that uses $\tilde{O}(k/\sqrt{\epsilon})$ matrix-vector products, improving on the na\"ive $\tilde{O}(k/\epsilon)$ dependence obtainable by the power method, where $\tilde{O}$ suppresses poly$(\log(dk/\epsilon))$ factors. Our main result is an algorithm that uses only $\tilde{O}(kp^{1/6}/\epsilon^{1/3})$ matrix-vector products, and works for all $p \geq 1$. For $p = 2$ our bound improves the previous $\tilde{O}(k/\epsilon^{1/2})$ bound to $\tilde{O}(k/\epsilon^{1/3})$. Since the Schatten-$p$ and Schatten-$\infty$ norms are the same up to a $1+ \epsilon$ factor when $p \geq (\log d)/\epsilon$, our bound recovers the result of Musco and Musco for $p = \infty$. Further, we prove a matrix-vector query lower bound of $\Omega(1/\epsilon^{1/3})$ for any fixed constant $p \geq 1$, showing that surprisingly $\tilde{\Theta}(1/\epsilon^{1/3})$ is the optimal complexity for constant~$k$. To obtain our results, we introduce several new techniques, including optimizing over multiple Krylov subspaces simultaneously, and pinching inequalities for partitioned operators. Our lower bound for $p \in [1,2]$ uses the Araki-Lieb-Thirring trace inequality, whereas for $p>2$, we appeal to a norm-compression inequality for aligned partitioned operators.

Quantum Topological Data Analysis with Linear Depth and Exponential Speedup

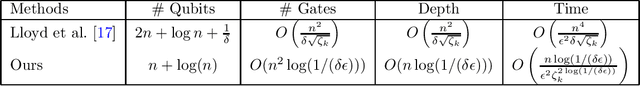
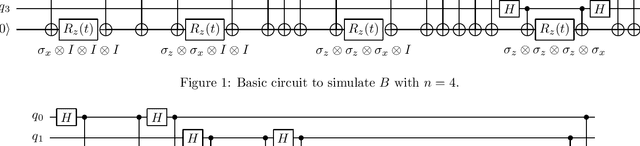
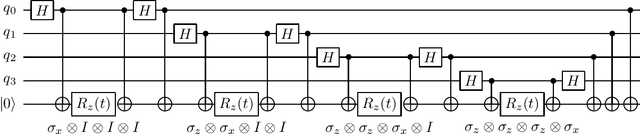
Quantum computing offers the potential of exponential speedups for certain classical computations. Over the last decade, many quantum machine learning (QML) algorithms have been proposed as candidates for such exponential improvements. However, two issues unravel the hope of exponential speedup for some of these QML algorithms: the data-loading problem and, more recently, the stunning dequantization results of Tang et al. A third issue, namely the fault-tolerance requirements of most QML algorithms, has further hindered their practical realization. The quantum topological data analysis (QTDA) algorithm of Lloyd, Garnerone and Zanardi was one of the first QML algorithms that convincingly offered an expected exponential speedup. From the outset, it did not suffer from the data-loading problem. A recent result has also shown that the generalized problem solved by this algorithm is likely classically intractable, and would therefore be immune to any dequantization efforts. However, the QTDA algorithm of Lloyd et~al. has a time complexity of $O(n^4/(\epsilon^2 \delta))$ (where $n$ is the number of data points, $\epsilon$ is the error tolerance, and $\delta$ is the smallest nonzero eigenvalue of the restricted Laplacian) and requires fault-tolerant quantum computing, which has not yet been achieved. In this paper, we completely overhaul the QTDA algorithm to achieve an improved exponential speedup and depth complexity of $O(n\log(1/(\delta\epsilon)))$. Our approach includes three key innovations: (a) an efficient realization of the combinatorial Laplacian as a sum of Pauli operators; (b) a quantum rejection sampling approach to restrict the superposition to the simplices in the complex; and (c) a stochastic rank estimation method to estimate the Betti numbers. We present a theoretical error analysis, and the circuit and computational time and depth complexities for Betti number estimation.

Near-Optimal Algorithms for Linear Algebra in the Current Matrix Multiplication Time

Currently, in the numerical linear algebra community, it is thought that to obtain nearly-optimal bounds for various problems such as rank computation, finding a maximal linearly independent subset of columns, regression, low rank approximation, maximum matching on general graphs and linear matroid union, one would need to resolve the main open question of Nelson and Nguyen (FOCS, 2013) regarding the logarithmic factors in the sketching dimension for existing constant factor approximation oblivious subspace embeddings. We show how to bypass this question using a refined sketching technique, and obtain optimal or nearly optimal bounds for these problems. A key technique we use is an explicit mapping of Indyk based on uncertainty principles and extractors, which after first applying known oblivious subspace embeddings, allows us to quickly spread out the mass of the vector so that sampling is now effective, and we avoid a logarithmic factor that is standard in the sketching dimension resulting from matrix Chernoff bounds. For the fundamental problems of rank computation and finding a linearly independent subset of columns, our algorithms improve Cheung, Kwok, and Lau (JACM, 2013) and are optimal to within a constant factor and a $\log\log(n)$-factor, respectively. Further, for constant factor regression and low rank approximation we give the first optimal algorithms, for the current matrix multiplication exponent.

Order Embeddings from Merged Ontologies using Sketching

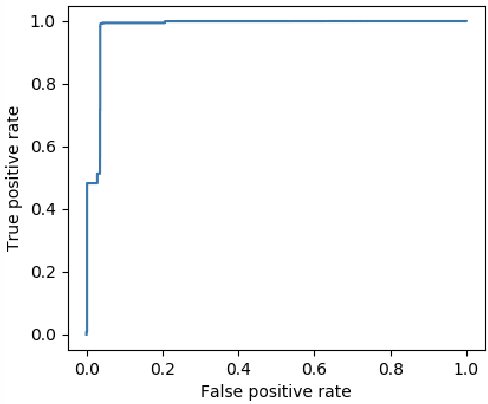
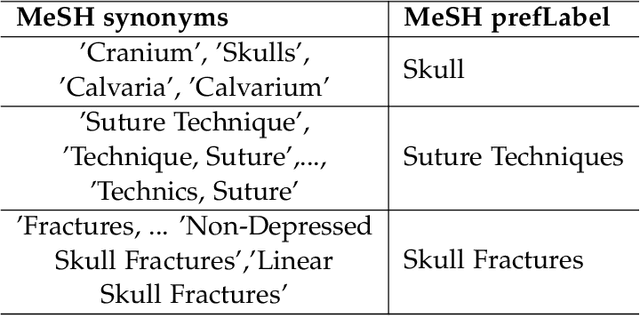
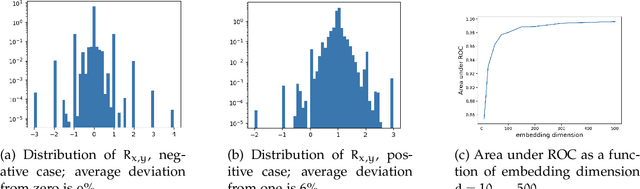
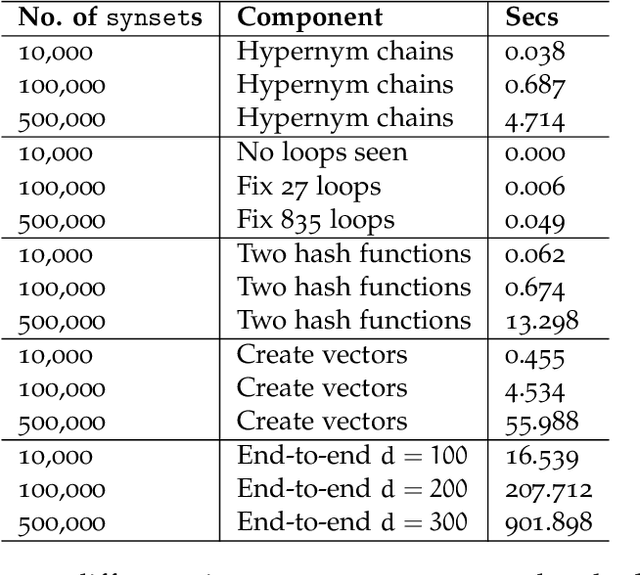
We give a simple, low resource method to produce order embeddings from ontologies. Such embeddings map words to vectors so that order relations on the words, such as hypernymy/hyponymy, are represented in a direct way. Our method uses sketching techniques, in particular countsketch, for dimensionality reduction. We also study methods to merge ontologies, in particular those in medical domains, so that order relations are preserved. We give computational results for medical ontologies and for wordnet, showing that our merging techniques are effective and our embedding yields an accurate representation in both generic and specialised domains.

Quantum-Inspired Algorithms from Randomized Numerical Linear Algebra

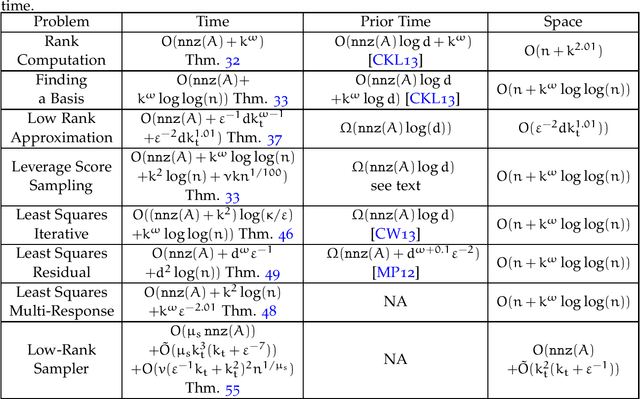
We create classical (non-quantum) dynamic data structures supporting queries for recommender systems and least-squares regression that are comparable to their quantum analogues. De-quantizing such algorithms has received a flurry of attention in recent years; we obtain sharper bounds for these problems. More significantly, we achieve these improvements by arguing that the previous quantum-inspired algorithms for these problems are doing leverage or ridge-leverage score sampling in disguise. With this recognition, we are able to employ the large body of work in numerical linear algebra to obtain algorithms for these problems that are simpler and faster than existing approaches. We also consider static data structures for the above problems, and obtain close-to-optimal bounds for them. To do this, we introduce a new randomized transform, the Gaussian Randomized Hadamard Transform (GRHT). It was thought in the numerical linear algebra community that to obtain nearly-optimal bounds for various problems such as rank computation, finding a maximal linearly independent subset of columns, regression, low rank approximation, maximum matching on general graphs and linear matroid union, that one would need to resolve the main open question of Nelson and Nguyen (FOCS, 2013) regarding the logarithmic factors in existing oblivious subspace embeddings. We bypass this question, using GRHT, and obtain optimal or nearly-optimal bounds for these problems. For the fundamental problems of rank computation and finding a linearly independent subset of columns, our algorithms improve Cheung, Kwok, and Lau (JACM, 2013) and are optimal to within a constant factor and a $\log\log(n)$-factor, respectively. Further, for constant factor regression and low rank approximation we give the first optimal algorithms, for the current matrix multiplication exponent.