Quantifying artificial intelligence through algebraic generalization

The rapid development of modern artificial intelligence (AI) systems has created an urgent need for their scientific quantification. While their fluency across a variety of domains is impressive, modern AI systems fall short on tests requiring symbolic processing and abstraction - a glaring limitation given the necessity for interpretable and reliable technology. Despite a surge of reasoning benchmarks emerging from the academic community, no comprehensive and theoretically-motivated framework exists to quantify reasoning (and more generally, symbolic ability) in AI systems. Here, we adopt a framework from computational complexity theory to explicitly quantify symbolic generalization: algebraic circuit complexity. Many symbolic reasoning problems can be recast as algebraic expressions. Thus, algebraic circuit complexity theory - the study of algebraic expressions as circuit models (i.e., directed acyclic graphs) - is a natural framework to study the complexity of symbolic computation. The tools of algebraic circuit complexity enable the study of generalization by defining benchmarks in terms of their complexity-theoretic properties (i.e., the difficulty of a problem). Moreover, algebraic circuits are generic mathematical objects; for a given algebraic circuit, an arbitrarily large number of samples can be generated for a specific circuit, making it an optimal testbed for the data-hungry machine learning algorithms that are used today. Here, we adopt tools from algebraic circuit complexity theory, apply it to formalize a science of symbolic generalization, and address key theoretical and empirical challenges for its successful application to AI science and its impact on the broader community.

Geometry of naturalistic object representations in recurrent neural network models of working memory

Working memory is a central cognitive ability crucial for intelligent decision-making. Recent experimental and computational work studying working memory has primarily used categorical (i.e., one-hot) inputs, rather than ecologically relevant, multidimensional naturalistic ones. Moreover, studies have primarily investigated working memory during single or few cognitive tasks. As a result, an understanding of how naturalistic object information is maintained in working memory in neural networks is still lacking. To bridge this gap, we developed sensory-cognitive models, comprising a convolutional neural network (CNN) coupled with a recurrent neural network (RNN), and trained them on nine distinct N-back tasks using naturalistic stimuli. By examining the RNN's latent space, we found that: (1) Multi-task RNNs represent both task-relevant and irrelevant information simultaneously while performing tasks; (2) The latent subspaces used to maintain specific object properties in vanilla RNNs are largely shared across tasks, but highly task-specific in gated RNNs such as GRU and LSTM; (3) Surprisingly, RNNs embed objects in new representational spaces in which individual object features are less orthogonalized relative to the perceptual space; (4) The transformation of working memory encodings (i.e., embedding of visual inputs in the RNN latent space) into memory was shared across stimuli, yet the transformations governing the retention of a memory in the face of incoming distractor stimuli were distinct across time. Our findings indicate that goal-driven RNNs employ chronological memory subspaces to track information over short time spans, enabling testable predictions with neural data.

The Importance of Positional Encoding Initialization in Transformers for Relational Reasoning

Relational reasoning refers to the ability to infer and understand the relations between multiple entities. In humans, this ability underpins many higher cognitive functions, such as problem solving and decision-making, and has been reliably linked to fluid intelligence. Despite machine learning models making impressive advances across various domains, such as natural language processing and vision, the extent to which such models can perform relational reasoning tasks remains unclear. Here we study the importance of positional encoding (PE) for relational reasoning in the Transformer, and find that a learnable PE outperforms all other commonly-used PEs (e.g., absolute, relative, rotary, etc.). Moreover, we find that when using a PE with a learnable parameter, the choice of initialization greatly influences the learned representations and its downstream generalization performance. Specifically, we find that a learned PE initialized from a small-norm distribution can 1) uncover ground-truth position information, 2) generalize in the presence of noisy inputs, and 3) produce behavioral patterns that are consistent with human performance. Our results shed light on the importance of learning high-performing and robust PEs during relational reasoning tasks, which will prove useful for tasks in which ground truth positions are not provided or not known.

On the generalization capacity of neural networks during generic multimodal reasoning

The advent of the Transformer has led to the development of large language models (LLM), which appear to demonstrate human-like capabilities. To assess the generality of this class of models and a variety of other base neural network architectures to multimodal domains, we evaluated and compared their capacity for multimodal generalization. We introduce a multimodal question-answer benchmark to evaluate three specific types of out-of-distribution (OOD) generalization performance: distractor generalization (generalization in the presence of distractors), systematic compositional generalization (generalization to new task permutations), and productive compositional generalization (generalization to more complex tasks structures). We found that across model architectures (e.g., RNNs, Transformers, Perceivers, etc.), models with multiple attention layers, or models that leveraged cross-attention mechanisms between input domains, fared better. Our positive results demonstrate that for multimodal distractor and systematic generalization, either cross-modal attention or models with deeper attention layers are key architectural features required to integrate multimodal inputs. On the other hand, neither of these architectural features led to productive generalization, suggesting fundamental limitations of existing architectures for specific types of multimodal generalization. These results demonstrate the strengths and limitations of specific architectural components underlying modern neural models for multimodal reasoning. Finally, we provide Generic COG (gCOG), a configurable benchmark with several multimodal generalization splits, for future studies to explore.

Predictive models of RNA degradation through dual crowdsourcing

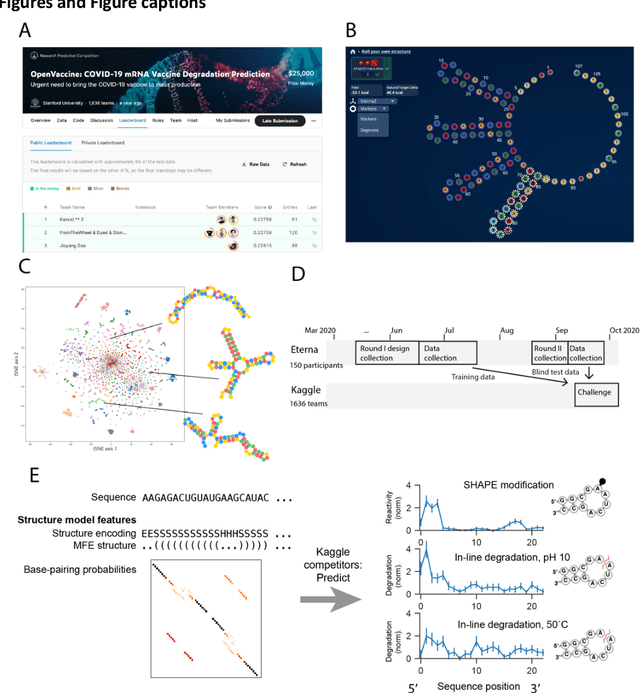
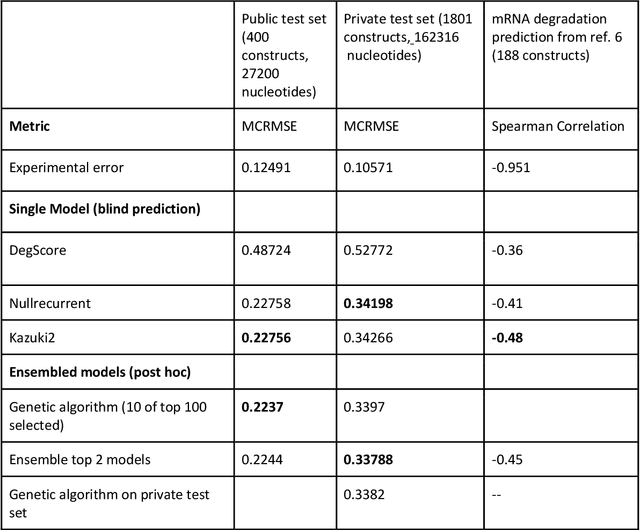
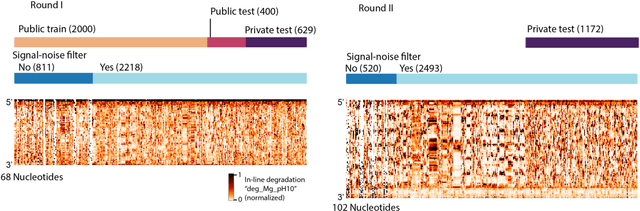
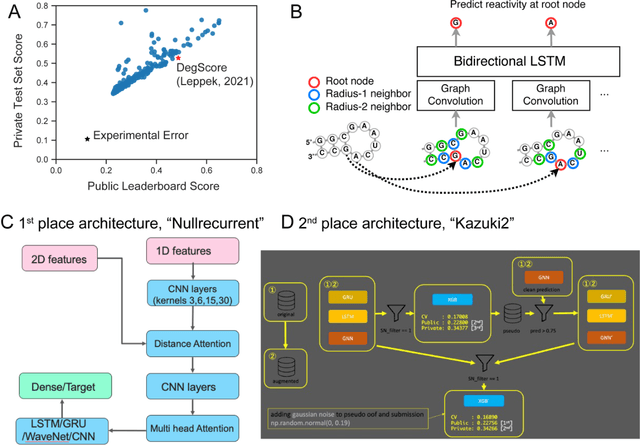
Messenger RNA-based medicines hold immense potential, as evidenced by their rapid deployment as COVID-19 vaccines. However, worldwide distribution of mRNA molecules has been limited by their thermostability, which is fundamentally limited by the intrinsic instability of RNA molecules to a chemical degradation reaction called in-line hydrolysis. Predicting the degradation of an RNA molecule is a key task in designing more stable RNA-based therapeutics. Here, we describe a crowdsourced machine learning competition ("Stanford OpenVaccine") on Kaggle, involving single-nucleotide resolution measurements on 6043 102-130-nucleotide diverse RNA constructs that were themselves solicited through crowdsourcing on the RNA design platform Eterna. The entire experiment was completed in less than 6 months. Winning models demonstrated test set errors that were better by 50% than the previous state-of-the-art DegScore model. Furthermore, these models generalized to blindly predicting orthogonal degradation data on much longer mRNA molecules (504-1588 nucleotides) with improved accuracy over DegScore and other models. Top teams integrated natural language processing architectures and data augmentation techniques with predictions from previous dynamic programming models for RNA secondary structure. These results indicate that such models are capable of representing in-line hydrolysis with excellent accuracy, supporting their use for designing stabilized messenger RNAs. The integration of two crowdsourcing platforms, one for data set creation and another for machine learning, may be fruitful for other urgent problems that demand scientific discovery on rapid timescales.