Recover: A Neuro-Symbolic Framework for Failure Detection and Recovery

Recognizing failures during task execution and implementing recovery procedures is challenging in robotics. Traditional approaches rely on the availability of extensive data or a tight set of constraints, while more recent approaches leverage large language models (LLMs) to verify task steps and replan accordingly. However, these methods often operate offline, necessitating scene resets and incurring in high costs. This paper introduces Recover, a neuro-symbolic framework for online failure identification and recovery. By integrating ontologies, logical rules, and LLM-based planners, Recover exploits symbolic information to enhance the ability of LLMs to generate recovery plans and also to decrease the associated costs. In order to demonstrate the capabilities of our method in a simulated kitchen environment, we introduce OntoThor, an ontology describing the AI2Thor simulator setting. Empirical evaluation shows that OntoThor's logical rules accurately detect all failures in the analyzed tasks, and that Recover considerably outperforms, for both failure detection and recovery, a baseline method reliant solely on LLMs.

AI Hilbert: From Data and Background Knowledge to Automated Scientific Discovery

The discovery of scientific formulae that parsimoniously explain natural phenomena and align with existing background theory is a key goal in science. Historically, scientists have derived natural laws by manipulating equations based on existing knowledge, forming new equations, and verifying them experimentally. In recent years, data-driven scientific discovery has emerged as a viable competitor in settings with large amounts of experimental data. Unfortunately, data-driven methods often fail to discover valid laws when data is noisy or scarce. Accordingly, recent works combine regression and reasoning to eliminate formulae inconsistent with background theory. However, the problem of searching over the space of formulae consistent with background theory to find one that fits the data best is not well solved. We propose a solution to this problem when all axioms and scientific laws are expressible via polynomial equalities and inequalities and argue that our approach is widely applicable. We further model notions of minimal complexity using binary variables and logical constraints, solve polynomial optimization problems via mixed-integer linear or semidefinite optimization, and automatically prove the validity of our scientific discoveries via Positivestellensatz certificates. Remarkably, the optimization techniques leveraged in this paper allow our approach to run in polynomial time with fully correct background theory, or non-deterministic polynomial (NP) time with partially correct background theory. We experimentally demonstrate that some famous scientific laws, including Kepler's Third Law of Planetary Motion, the Hagen-Poiseuille Equation, and the Radiated Gravitational Wave Power equation, can be automatically derived from sets of partially correct background axioms.

Bayesian Experimental Design for Symbolic Discovery

This study concerns the formulation and application of Bayesian optimal experimental design to symbolic discovery, which is the inference from observational data of predictive models taking general functional forms. We apply constrained first-order methods to optimize an appropriate selection criterion, using Hamiltonian Monte Carlo to sample from the prior. A step for computing the predictive distribution, involving convolution, is computed via either numerical integration, or via fast transform methods.

Integration of Data and Theory for Accelerated Derivable Symbolic Discovery

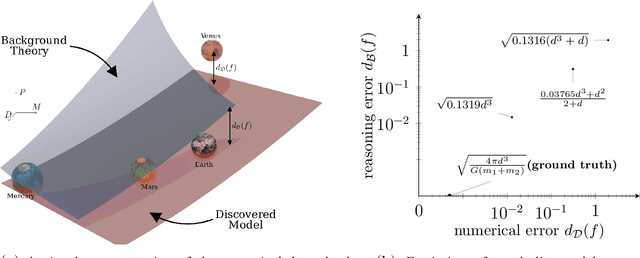
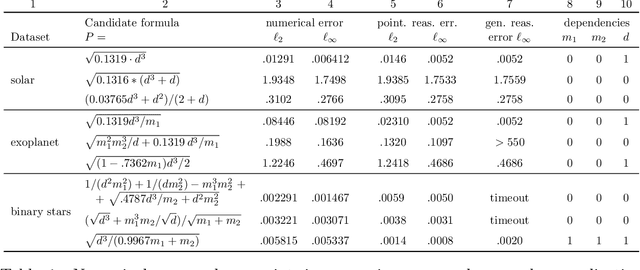
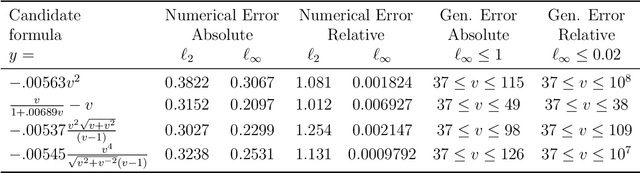
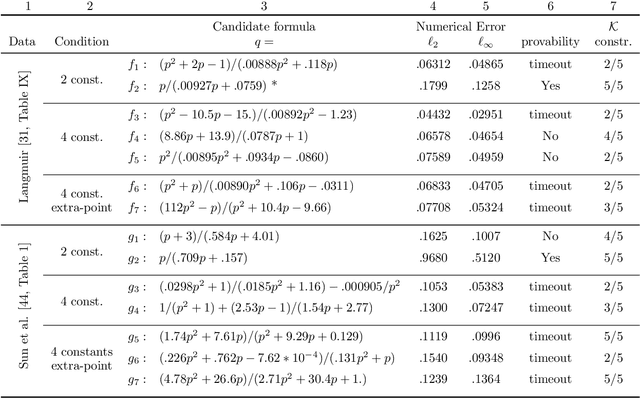
Scientists have long aimed to discover meaningful equations which accurately describe data. Machine learning algorithms automate construction of accurate data-driven models, but ensuring that these are consistent with existing knowledge is a challenge. We developed a methodology combining automated theorem proving with symbolic regression, enabling principled derivations of laws of nature. We demonstrate this for Kepler's third law, Einstein's relativistic time dilation, and Langmuir's theory of adsorption, in each case, automatically connecting experimental data with background theory. The combination of logical reasoning with machine learning provides generalizable insights into key aspects of the natural phenomena.

Learning to Guide a Saturation-Based Theorem Prover

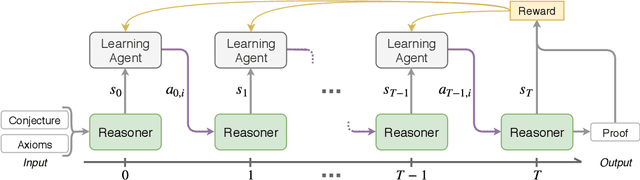
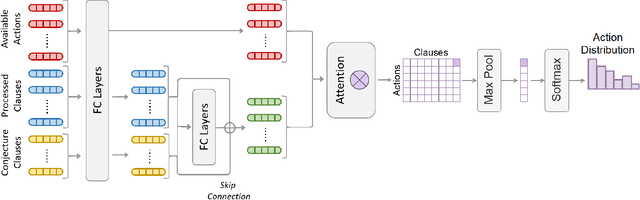
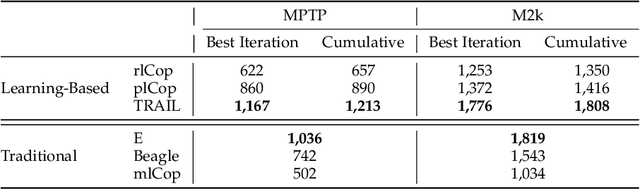
Traditional automated theorem provers have relied on manually tuned heuristics to guide how they perform proof search. Recently, however, there has been a surge of interest in the design of learning mechanisms that can be integrated into theorem provers to improve their performance automatically. In this work, we introduce TRAIL, a deep learning-based approach to theorem proving that characterizes core elements of saturation-based theorem proving within a neural framework. TRAIL leverages (a) an effective graph neural network for representing logical formulas, (b) a novel neural representation of the state of a saturation-based theorem prover in terms of processed clauses and available actions, and (c) a novel representation of the inference selection process as an attention-based action policy. We show through a systematic analysis that these components allow TRAIL to significantly outperform previous reinforcement learning-based theorem provers on two standard benchmark datasets (up to 36% more theorems proved). In addition, to the best of our knowledge, TRAIL is the first reinforcement learning-based approach to exceed the performance of a state-of-the-art traditional theorem prover on a standard theorem proving benchmark (solving up to 17% more problems).

Question Answering over Knowledge Bases by Leveraging Semantic Parsing and Neuro-Symbolic Reasoning

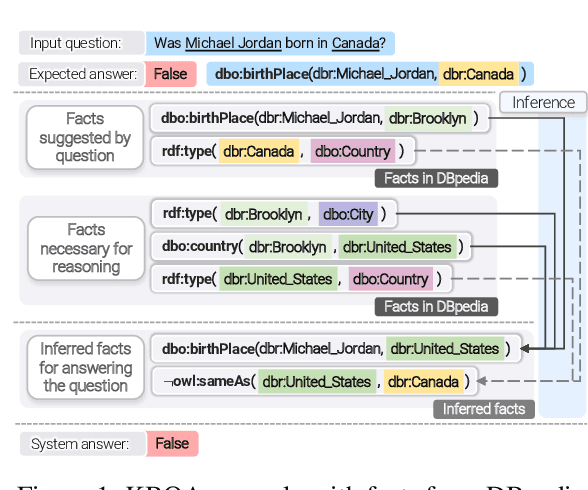
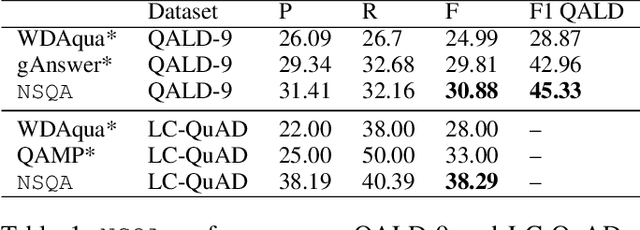
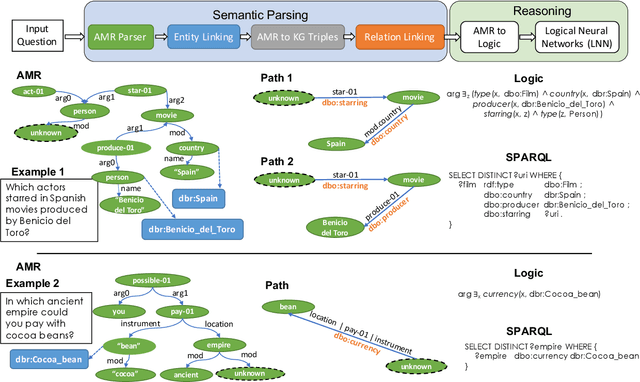
Knowledge base question answering (KBQA) is an important task in Natural Language Processing. Existing approaches face significant challenges including complex question understanding, necessity for reasoning, and lack of large training datasets. In this work, we propose a semantic parsing and reasoning-based Neuro-Symbolic Question Answering(NSQA) system, that leverages (1) Abstract Meaning Representation (AMR) parses for task-independent question under-standing; (2) a novel path-based approach to transform AMR parses into candidate logical queries that are aligned to the KB; (3) a neuro-symbolic reasoner called Logical Neural Net-work (LNN) that executes logical queries and reasons over KB facts to provide an answer; (4) system of systems approach,which integrates multiple, reusable modules that are trained specifically for their individual tasks (e.g. semantic parsing,entity linking, and relationship linking) and do not require end-to-end training data. NSQA achieves state-of-the-art performance on QALD-9 and LC-QuAD 1.0. NSQA's novelty lies in its modular neuro-symbolic architecture and its task-general approach to interpreting natural language questions.

Symbolic Regression using Mixed-Integer Nonlinear Optimization

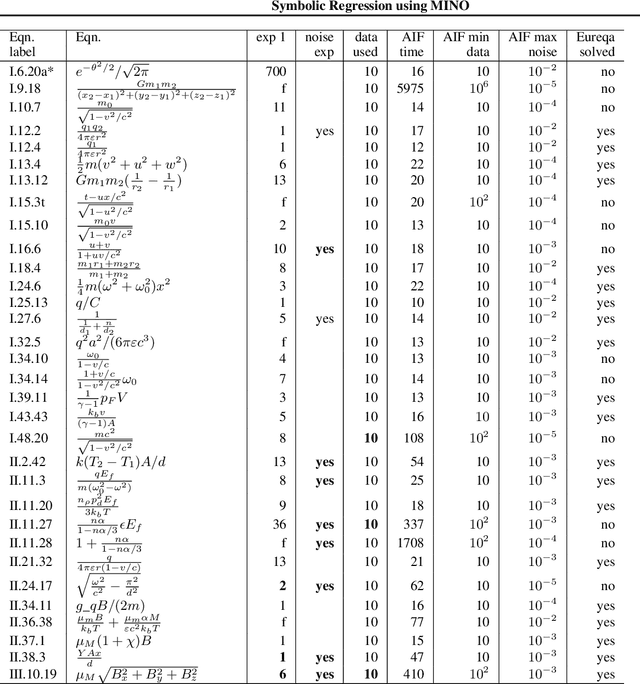
The Symbolic Regression (SR) problem, where the goal is to find a regression function that does not have a pre-specified form but is any function that can be composed of a list of operators, is a hard problem in machine learning, both theoretically and computationally. Genetic programming based methods, that heuristically search over a very large space of functions, are the most commonly used methods to tackle SR problems. An alternative mathematical programming approach, proposed in the last decade, is to express the optimal symbolic expression as the solution of a system of nonlinear equations over continuous and discrete variables that minimizes a certain objective, and to solve this system via a global solver for mixed-integer nonlinear programming problems. Algorithms based on the latter approach are often very slow. We propose a hybrid algorithm that combines mixed-integer nonlinear optimization with explicit enumeration and incorporates constraints from dimensional analysis. We show that our algorithm is competitive, for some synthetic data sets, with a state-of-the-art SR software and a recent physics-inspired method called AI Feynman.

Schemaless Queries over Document Tables with Dependencies

Unstructured enterprise data such as reports, manuals and guidelines often contain tables. The traditional way of integrating data from these tables is through a two-step process of table detection/extraction and mapping the table layouts to an appropriate schema. This can be an expensive process. In this paper we show that by using semantic technologies (RDF/SPARQL and database dependencies) paired with a simple but powerful way to transform tables with non-relational layouts, it is possible to offer query answering services over these tables with minimal manual work or domain-specific mappings. Our method enables users to exploit data in tables embedded in documents with little effort, not only for simple retrieval queries, but also for structured queries that require joining multiple interrelated tables.

Improving Graph Neural Network Representations of Logical Formulae with Subgraph Pooling

Recent advances in the integration of deep learning with automated theorem proving have centered around the representation of logical formulae as inputs to deep learning systems. In particular, there has been a shift from character and token-level representations to graph-structured representations, in large part driven by the rapidly emerging body of research on geometric deep learning. Typically, structure-aware neural methods for embedding logical formulae have been variants of either Tree LSTMs or GNNs. While more effective than character and token-level approaches, such methods have often made representational trade-offs that limited their ability to effectively represent the global structure of their inputs. In this work, we introduce a novel approach for embedding logical formulae using DAG LSTMs that is designed to overcome the limitations of both Tree LSTMs and GNNs. The effectiveness of the proposed framework is demonstrated on the tasks of premise selection and proof step classification where it achieves the state-of-the-art performance on two standard datasets.

A Deep Reinforcement Learning based Approach to Learning Transferable Proof Guidance Strategies

Traditional first-order logic (FOL) reasoning systems usually rely on manual heuristics for proof guidance. We propose TRAIL: a system that learns to perform proof guidance using reinforcement learning. A key design principle of our system is that it is general enough to allow transfer to problems in different domains that do not share the same vocabulary of the training set. To do so, we developed a novel representation of the internal state of a prover in terms of clauses and inference actions, and a novel neural-based attention mechanism to learn interactions between clauses. We demonstrate that this approach enables the system to generalize from training to test data across domains with different vocabularies, suggesting that the neural architecture in TRAIL is well suited for representing and processing of logical formalisms.