An Efficient Interior-Point Method for Online Convex Optimization

A new algorithm for regret minimization in online convex optimization is described. The regret of the algorithm after $T$ time periods is $O(\sqrt{T \log T})$ - which is the minimum possible up to a logarithmic term. In addition, the new algorithm is adaptive, in the sense that the regret bounds hold not only for the time periods $1,\ldots,T$ but also for every sub-interval $s,s+1,\ldots,t$. The running time of the algorithm matches that of newly introduced interior point algorithms for regret minimization: in $n$-dimensional space, during each iteration the new algorithm essentially solves a system of linear equations of order $n$, rather than solving some constrained convex optimization problem in $n$ dimensions and possibly many constraints.

On "Indifference" and Backward Induction in Games with Perfect Information

Indifference of a player with respect to two distinct outcomes of a game cannot be handled by small perturbations, because the actual choice may have significant impact on other players, and cause them to act in a way that has significant impact of the indifferent player. It is argued that ties among rational choices can be resolved by refinements of the concept of rationality based on the utilities of other players. One such refinement is the concept of Tit-for-Tat.

On the Use of Generative Models in Observational Causal Analysis

The use of a hypothetical generative model was been suggested for causal analysis of observational data. The very assumption of a particular model is a commitment to a certain set of variables and therefore to a certain set of possible causes. Estimating the joint probability distribution of can be useful for predicting values of variables in view of the observed values of others, but it is not sufficient for inferring causal relationships. The model describes a single observable distribution and cannot a chain of effects of intervention that deviate from the observed distribution.

Remarks on Utility in Repeated Bets

The use of von Neumann -- Morgenstern utility is examined in the context of multiple choices between lotteries. Different conclusions are reached if the choices are simultaneous or sequential. It is demonstrated that utility cannot be additive.

Bayesian Experimental Design for Symbolic Discovery

This study concerns the formulation and application of Bayesian optimal experimental design to symbolic discovery, which is the inference from observational data of predictive models taking general functional forms. We apply constrained first-order methods to optimize an appropriate selection criterion, using Hamiltonian Monte Carlo to sample from the prior. A step for computing the predictive distribution, involving convolution, is computed via either numerical integration, or via fast transform methods.

Integration of Data and Theory for Accelerated Derivable Symbolic Discovery

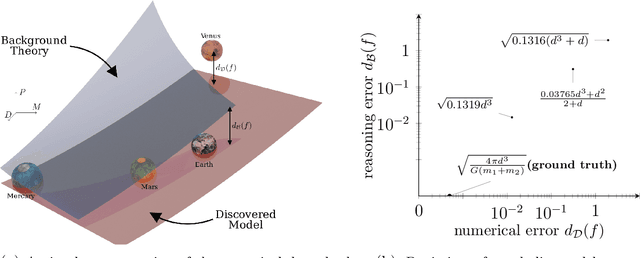
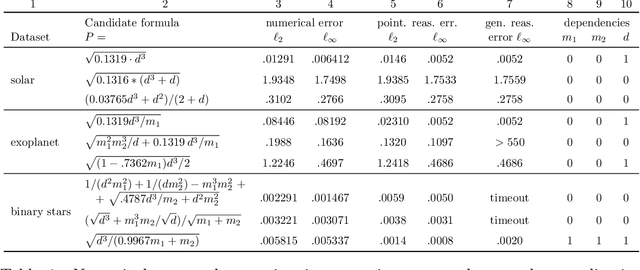
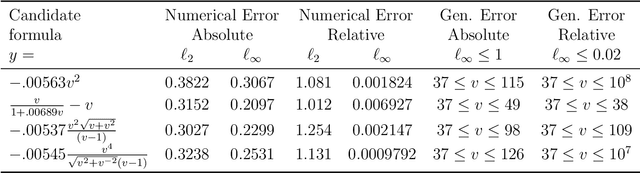
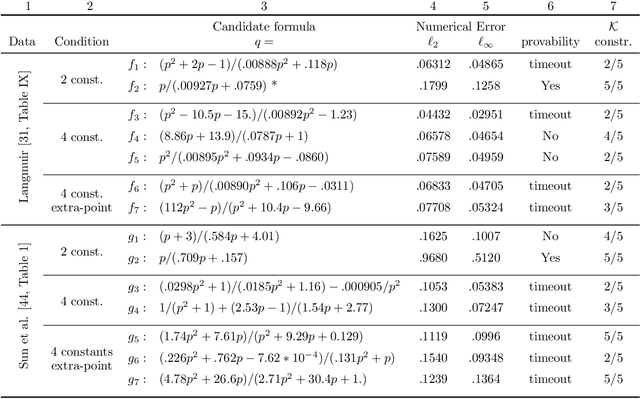
Scientists have long aimed to discover meaningful equations which accurately describe data. Machine learning algorithms automate construction of accurate data-driven models, but ensuring that these are consistent with existing knowledge is a challenge. We developed a methodology combining automated theorem proving with symbolic regression, enabling principled derivations of laws of nature. We demonstrate this for Kepler's third law, Einstein's relativistic time dilation, and Langmuir's theory of adsorption, in each case, automatically connecting experimental data with background theory. The combination of logical reasoning with machine learning provides generalizable insights into key aspects of the natural phenomena.

Symbolic Regression using Mixed-Integer Nonlinear Optimization

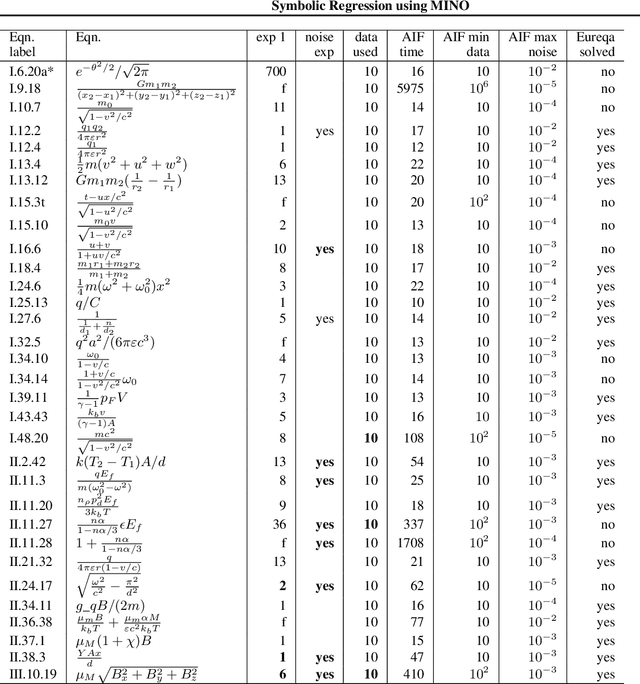
The Symbolic Regression (SR) problem, where the goal is to find a regression function that does not have a pre-specified form but is any function that can be composed of a list of operators, is a hard problem in machine learning, both theoretically and computationally. Genetic programming based methods, that heuristically search over a very large space of functions, are the most commonly used methods to tackle SR problems. An alternative mathematical programming approach, proposed in the last decade, is to express the optimal symbolic expression as the solution of a system of nonlinear equations over continuous and discrete variables that minimizes a certain objective, and to solve this system via a global solver for mixed-integer nonlinear programming problems. Algorithms based on the latter approach are often very slow. We propose a hybrid algorithm that combines mixed-integer nonlinear optimization with explicit enumeration and incorporates constraints from dimensional analysis. We show that our algorithm is competitive, for some synthetic data sets, with a state-of-the-art SR software and a recent physics-inspired method called AI Feynman.

Strategic Classification

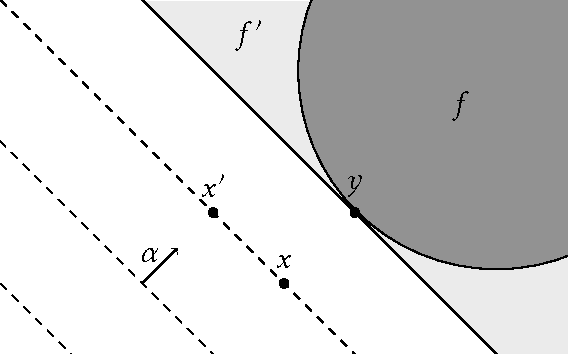
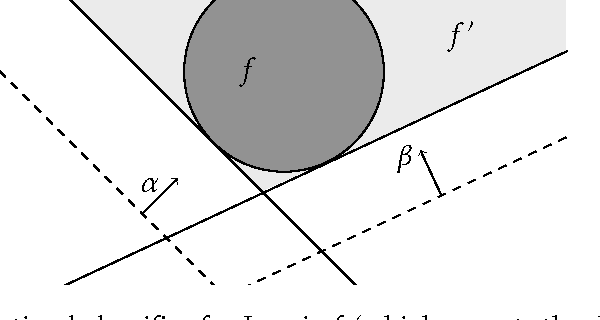
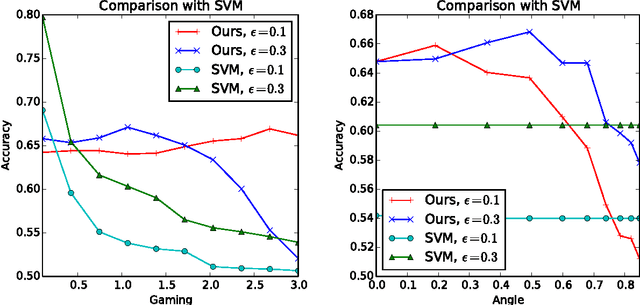
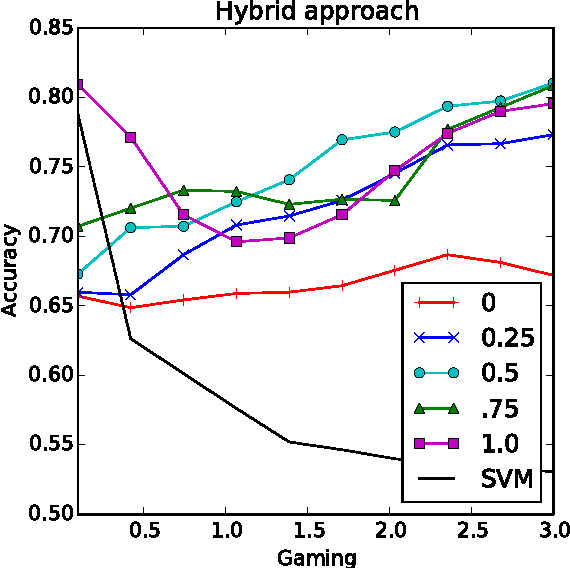
Machine learning relies on the assumption that unseen test instances of a classification problem follow the same distribution as observed training data. However, this principle can break down when machine learning is used to make important decisions about the welfare (employment, education, health) of strategic individuals. Knowing information about the classifier, such individuals may manipulate their attributes in order to obtain a better classification outcome. As a result of this behavior---often referred to as gaming---the performance of the classifier may deteriorate sharply. Indeed, gaming is a well-known obstacle for using machine learning methods in practice; in financial policy-making, the problem is widely known as Goodhart's law. In this paper, we formalize the problem, and pursue algorithms for learning classifiers that are robust to gaming. We model classification as a sequential game between a player named "Jury" and a player named "Contestant." Jury designs a classifier, and Contestant receives an input to the classifier, which he may change at some cost. Jury's goal is to achieve high classification accuracy with respect to Contestant's original input and some underlying target classification function. Contestant's goal is to achieve a favorable classification outcome while taking into account the cost of achieving it. For a natural class of cost functions, we obtain computationally efficient learning algorithms which are near-optimal. Surprisingly, our algorithms are efficient even on concept classes that are computationally hard to learn. For general cost functions, designing an approximately optimal strategy-proof classifier, for inverse-polynomial approximation, is NP-hard.