Hierarchical Planning for Complex Tasks with Knowledge Graph-RAG and Symbolic Verification

Large Language Models (LLMs) have shown promise as robotic planners but often struggle with long-horizon and complex tasks, especially in specialized environments requiring external knowledge. While hierarchical planning and Retrieval-Augmented Generation (RAG) address some of these challenges, they remain insufficient on their own and a deeper integration is required for achieving more reliable systems. To this end, we propose a neuro-symbolic approach that enhances LLMs-based planners with Knowledge Graph-based RAG for hierarchical plan generation. This method decomposes complex tasks into manageable subtasks, further expanded into executable atomic action sequences. To ensure formal correctness and proper decomposition, we integrate a Symbolic Validator, which also functions as a failure detector by aligning expected and observed world states. Our evaluation against baseline methods demonstrates the consistent significant advantages of integrating hierarchical planning, symbolic verification, and RAG across tasks of varying complexity and different LLMs. Additionally, our experimental setup and novel metrics not only validate our approach for complex planning but also serve as a tool for assessing LLMs' reasoning and compositional capabilities.

Assessing the Emergent Symbolic Reasoning Abilities of Llama Large Language Models

Large Language Models (LLMs) achieve impressive performance in a wide range of tasks, even if they are often trained with the only objective of chatting fluently with users. Among other skills, LLMs show emergent abilities in mathematical reasoning benchmarks, which can be elicited with appropriate prompting methods. In this work, we systematically investigate the capabilities and limitations of popular open-source LLMs on different symbolic reasoning tasks. We evaluate three models of the Llama 2 family on two datasets that require solving mathematical formulas of varying degrees of difficulty. We test a generalist LLM (Llama 2 Chat) as well as two fine-tuned versions of Llama 2 (MAmmoTH and MetaMath) specifically designed to tackle mathematical problems. We observe that both increasing the scale of the model and fine-tuning it on relevant tasks lead to significant performance gains. Furthermore, using fine-grained evaluation measures, we find that such performance gains are mostly observed with mathematical formulas of low complexity, which nevertheless often remain challenging even for the largest fine-tuned models.

Benchmarking GPT-4 on Algorithmic Problems: A Systematic Evaluation of Prompting Strategies

Large Language Models (LLMs) have revolutionized the field of Natural Language Processing thanks to their ability to reuse knowledge acquired on massive text corpora on a wide variety of downstream tasks, with minimal (if any) tuning steps. At the same time, it has been repeatedly shown that LLMs lack systematic generalization, which allows to extrapolate the learned statistical regularities outside the training distribution. In this work, we offer a systematic benchmarking of GPT-4, one of the most advanced LLMs available, on three algorithmic tasks characterized by the possibility to control the problem difficulty with two parameters. We compare the performance of GPT-4 with that of its predecessor (GPT-3.5) and with a variant of the Transformer-Encoder architecture recently introduced to solve similar tasks, the Neural Data Router. We find that the deployment of advanced prompting techniques allows GPT-4 to reach superior accuracy on all tasks, demonstrating that state-of-the-art LLMs constitute a very strong baseline also in challenging tasks that require systematic generalization.

A Neural Rewriting System to Solve Algorithmic Problems

Modern neural network architectures still struggle to learn algorithmic procedures that require to systematically apply compositional rules to solve out-of-distribution problem instances. In this work, we propose an original approach to learn algorithmic tasks inspired by rewriting systems, a classic framework in symbolic artificial intelligence. We show that a rewriting system can be implemented as a neural architecture composed by specialized modules: the Selector identifies the target sub-expression to process, the Solver simplifies the sub-expression by computing the corresponding result, and the Combiner produces a new version of the original expression by replacing the sub-expression with the solution provided. We evaluate our model on three types of algorithmic tasks that require simplifying symbolic formulas involving lists, arithmetic, and algebraic expressions. We test the extrapolation capabilities of the proposed architecture using formulas involving a higher number of operands and nesting levels than those seen during training, and we benchmark its performance against the Neural Data Router, a recent model specialized for systematic generalization, and a state-of-the-art large language model (GPT-4) probed with advanced prompting strategies.

A Hybrid System for Systematic Generalization in Simple Arithmetic Problems

Solving symbolic reasoning problems that require compositionality and systematicity is considered one of the key ingredients of human intelligence. However, symbolic reasoning is still a great challenge for deep learning models, which often cannot generalize the reasoning pattern to out-of-distribution test cases. In this work, we propose a hybrid system capable of solving arithmetic problems that require compositional and systematic reasoning over sequences of symbols. The model acquires such a skill by learning appropriate substitution rules, which are applied iteratively to the input string until the expression is completely resolved. We show that the proposed system can accurately solve nested arithmetical expressions even when trained only on a subset including the simplest cases, significantly outperforming both a sequence-to-sequence model trained end-to-end and a state-of-the-art large language model.

Learning to solve arithmetic problems with a virtual abacus

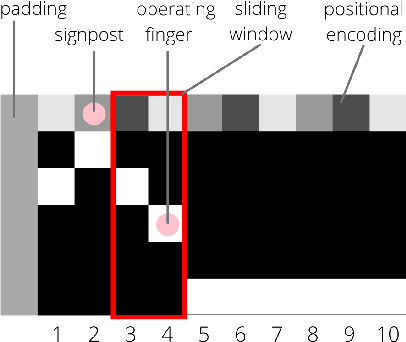
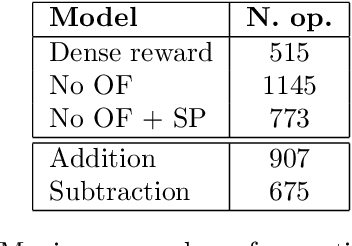
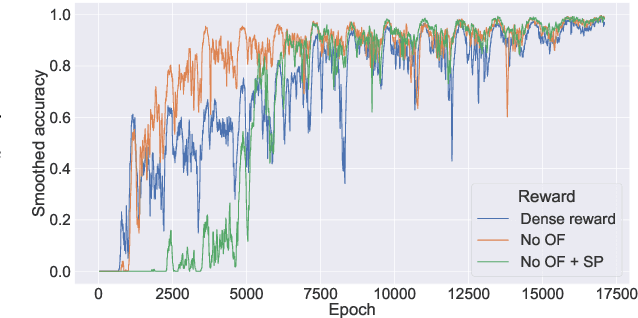
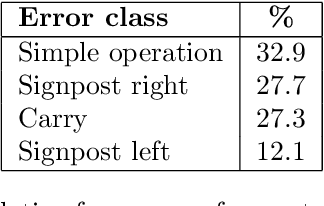
Acquiring mathematical skills is considered a key challenge for modern Artificial Intelligence systems. Inspired by the way humans discover numerical knowledge, here we introduce a deep reinforcement learning framework that allows to simulate how cognitive agents could gradually learn to solve arithmetic problems by interacting with a virtual abacus. The proposed model successfully learn to perform multi-digit additions and subtractions, achieving an error rate below 1% even when operands are much longer than those observed during training. We also compare the performance of learning agents receiving a different amount of explicit supervision, and we analyze the most common error patterns to better understand the limitations and biases resulting from our design choices.