Estimating the distribution of numerosity and non-numerical visual magnitudes in natural scenes using computer vision

Humans share with many animal species the ability to perceive and approximately represent the number of objects in visual scenes. This ability improves throughout childhood, suggesting that learning and development play a key role in shaping our number sense. This hypothesis is further supported by computational investigations based on deep learning, which have shown that numerosity perception can spontaneously emerge in neural networks that learn the statistical structure of images with a varying number of items. However, neural network models are usually trained using synthetic datasets that might not faithfully reflect the statistical structure of natural environments. In this work, we exploit recent advances in computer vision algorithms to design and implement an original pipeline that can be used to estimate the distribution of numerosity and non-numerical magnitudes in large-scale datasets containing thousands of real images depicting objects in daily life situations. We show that in natural visual scenes the frequency of appearance of different numerosities follows a power law distribution and that numerosity is strongly correlated with many continuous magnitudes, such as cumulative areas and convex hull, which might explain why numerosity judgements are often influenced by these non-numerical cues.

Assessing the Emergent Symbolic Reasoning Abilities of Llama Large Language Models

Large Language Models (LLMs) achieve impressive performance in a wide range of tasks, even if they are often trained with the only objective of chatting fluently with users. Among other skills, LLMs show emergent abilities in mathematical reasoning benchmarks, which can be elicited with appropriate prompting methods. In this work, we systematically investigate the capabilities and limitations of popular open-source LLMs on different symbolic reasoning tasks. We evaluate three models of the Llama 2 family on two datasets that require solving mathematical formulas of varying degrees of difficulty. We test a generalist LLM (Llama 2 Chat) as well as two fine-tuned versions of Llama 2 (MAmmoTH and MetaMath) specifically designed to tackle mathematical problems. We observe that both increasing the scale of the model and fine-tuning it on relevant tasks lead to significant performance gains. Furthermore, using fine-grained evaluation measures, we find that such performance gains are mostly observed with mathematical formulas of low complexity, which nevertheless often remain challenging even for the largest fine-tuned models.

A Neural Rewriting System to Solve Algorithmic Problems

Modern neural network architectures still struggle to learn algorithmic procedures that require to systematically apply compositional rules to solve out-of-distribution problem instances. In this work, we propose an original approach to learn algorithmic tasks inspired by rewriting systems, a classic framework in symbolic artificial intelligence. We show that a rewriting system can be implemented as a neural architecture composed by specialized modules: the Selector identifies the target sub-expression to process, the Solver simplifies the sub-expression by computing the corresponding result, and the Combiner produces a new version of the original expression by replacing the sub-expression with the solution provided. We evaluate our model on three types of algorithmic tasks that require simplifying symbolic formulas involving lists, arithmetic, and algebraic expressions. We test the extrapolation capabilities of the proposed architecture using formulas involving a higher number of operands and nesting levels than those seen during training, and we benchmark its performance against the Neural Data Router, a recent model specialized for systematic generalization, and a state-of-the-art large language model (GPT-4) probed with advanced prompting strategies.

Benchmarking GPT-4 on Algorithmic Problems: A Systematic Evaluation of Prompting Strategies

Large Language Models (LLMs) have revolutionized the field of Natural Language Processing thanks to their ability to reuse knowledge acquired on massive text corpora on a wide variety of downstream tasks, with minimal (if any) tuning steps. At the same time, it has been repeatedly shown that LLMs lack systematic generalization, which allows to extrapolate the learned statistical regularities outside the training distribution. In this work, we offer a systematic benchmarking of GPT-4, one of the most advanced LLMs available, on three algorithmic tasks characterized by the possibility to control the problem difficulty with two parameters. We compare the performance of GPT-4 with that of its predecessor (GPT-3.5) and with a variant of the Transformer-Encoder architecture recently introduced to solve similar tasks, the Neural Data Router. We find that the deployment of advanced prompting techniques allows GPT-4 to reach superior accuracy on all tasks, demonstrating that state-of-the-art LLMs constitute a very strong baseline also in challenging tasks that require systematic generalization.

A Hybrid System for Systematic Generalization in Simple Arithmetic Problems

Solving symbolic reasoning problems that require compositionality and systematicity is considered one of the key ingredients of human intelligence. However, symbolic reasoning is still a great challenge for deep learning models, which often cannot generalize the reasoning pattern to out-of-distribution test cases. In this work, we propose a hybrid system capable of solving arithmetic problems that require compositional and systematic reasoning over sequences of symbols. The model acquires such a skill by learning appropriate substitution rules, which are applied iteratively to the input string until the expression is completely resolved. We show that the proposed system can accurately solve nested arithmetical expressions even when trained only on a subset including the simplest cases, significantly outperforming both a sequence-to-sequence model trained end-to-end and a state-of-the-art large language model.

Investigating the generative dynamics of energy-based neural networks

Generative neural networks can produce data samples according to the statistical properties of their training distribution. This feature can be used to test modern computational neuroscience hypotheses suggesting that spontaneous brain activity is partially supported by top-down generative processing. A widely studied class of generative models is that of Restricted Boltzmann Machines (RBMs), which can be used as building blocks for unsupervised deep learning architectures. In this work, we systematically explore the generative dynamics of RBMs, characterizing the number of states visited during top-down sampling and investigating whether the heterogeneity of visited attractors could be increased by starting the generation process from biased hidden states. By considering an RBM trained on a classic dataset of handwritten digits, we show that the capacity to produce diverse data prototypes can be increased by initiating top-down sampling from chimera states, which encode high-level visual features of multiple digits. We also found that the model is not capable of transitioning between all possible digit states within a single generation trajectory, suggesting that the top-down dynamics is heavily constrained by the shape of the energy function.

Can neural networks do arithmetic? A survey on the elementary numerical skills of state-of-the-art deep learning models

Creating learning models that can exhibit sophisticated reasoning skills is one of the greatest challenges in deep learning research, and mathematics is rapidly becoming one of the target domains for assessing scientific progress in this direction. In the past few years there has been an explosion of neural network architectures, data sets, and benchmarks specifically designed to tackle mathematical problems, reporting notable success in disparate fields such as automated theorem proving, numerical integration, and discovery of new conjectures or matrix multiplication algorithms. However, despite these impressive achievements it is still unclear whether deep learning models possess an elementary understanding of quantities and symbolic numbers. In this survey we critically examine the recent literature, concluding that even state-of-the-art architectures often fall short when probed with relatively simple tasks designed to test basic numerical and arithmetic knowledge.

Learning to solve arithmetic problems with a virtual abacus

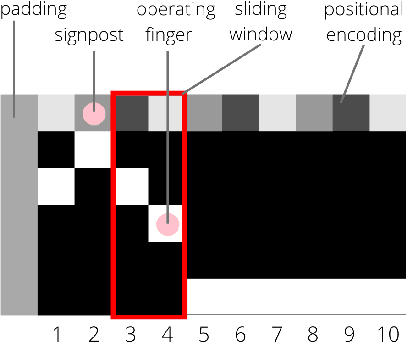
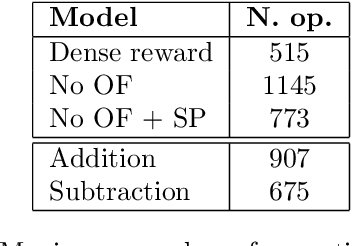
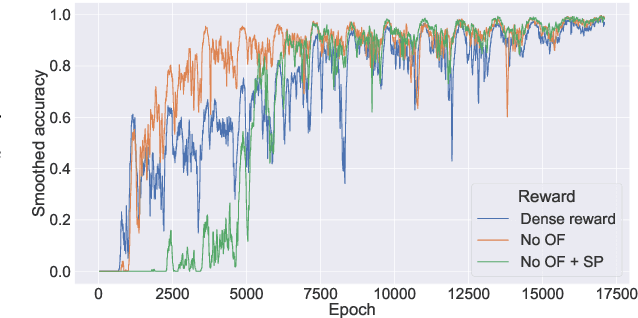
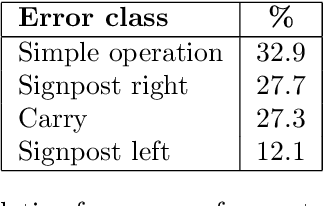
Acquiring mathematical skills is considered a key challenge for modern Artificial Intelligence systems. Inspired by the way humans discover numerical knowledge, here we introduce a deep reinforcement learning framework that allows to simulate how cognitive agents could gradually learn to solve arithmetic problems by interacting with a virtual abacus. The proposed model successfully learn to perform multi-digit additions and subtractions, achieving an error rate below 1% even when operands are much longer than those observed during training. We also compare the performance of learning agents receiving a different amount of explicit supervision, and we analyze the most common error patterns to better understand the limitations and biases resulting from our design choices.

Automated Detection of Dolphin Whistles with Convolutional Networks and Transfer Learning

Effective conservation of maritime environments and wildlife management of endangered species require the implementation of efficient, accurate and scalable solutions for environmental monitoring. Ecoacoustics offers the advantages of non-invasive, long-duration sampling of environmental sounds and has the potential to become the reference tool for biodiversity surveying. However, the analysis and interpretation of acoustic data is a time-consuming process that often requires a great amount of human supervision. This issue might be tackled by exploiting modern techniques for automatic audio signal analysis, which have recently achieved impressive performance thanks to the advances in deep learning research. In this paper we show that convolutional neural networks can indeed significantly outperform traditional automatic methods in a challenging detection task: identification of dolphin whistles from underwater audio recordings. The proposed system can detect signals even in the presence of ambient noise, at the same time consistently reducing the likelihood of producing false positives and false negatives. Our results further support the adoption of artificial intelligence technology to improve the automatic monitoring of marine ecosystems.

A developmental approach for training deep belief networks

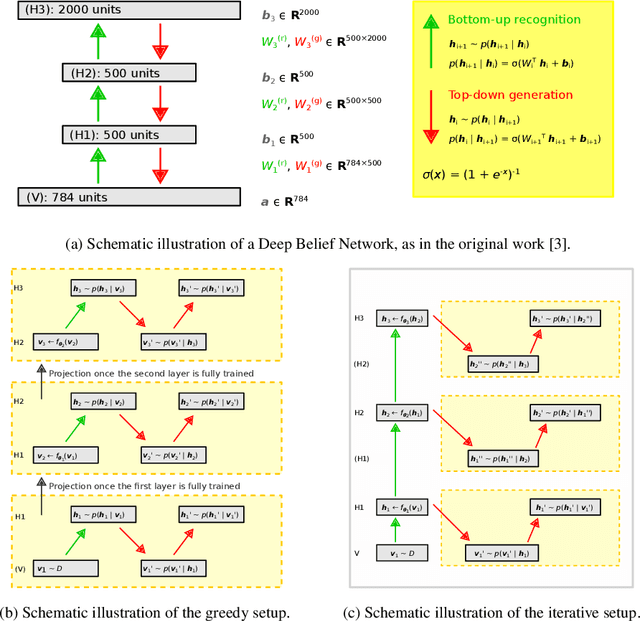
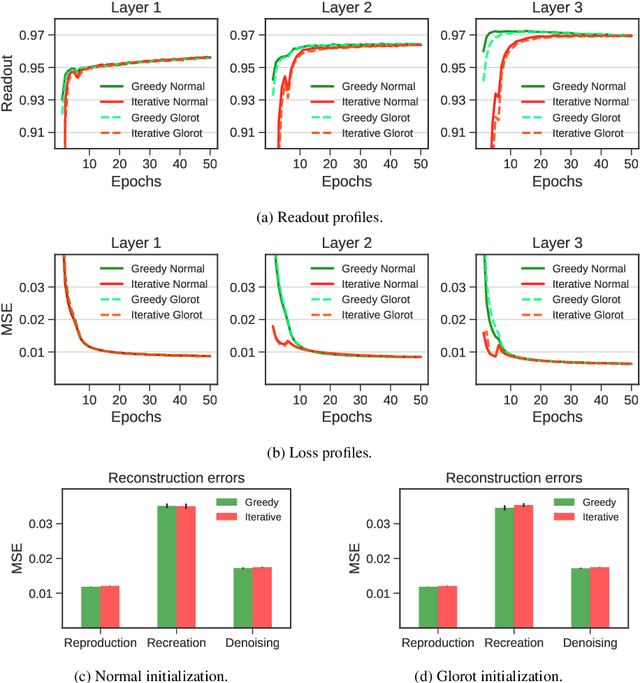
Deep belief networks (DBNs) are stochastic neural networks that can extract rich internal representations of the environment from the sensory data. DBNs had a catalytic effect in triggering the deep learning revolution, demonstrating for the very first time the feasibility of unsupervised learning in networks with many layers of hidden neurons. Thanks to their biological and cognitive plausibility, these hierarchical architectures have been also successfully exploited to build computational models of human perception and cognition in a variety of domains. However, learning in DBNs is usually carried out in a greedy, layer-wise fashion, which does not allow to simulate the holistic development of cortical circuits. Here we present iDBN, an iterative learning algorithm for DBNs that allows to jointly update the connection weights across all layers of the hierarchy. We test our algorithm on two different sets of visual stimuli, and we show that network development can also be tracked in terms of graph theoretical properties. DBNs trained using our iterative approach achieve a final performance comparable to that of the greedy counterparts, at the same time allowing to accurately analyze the gradual development of internal representations in the generative model. Our work paves the way to the use of iDBN for modeling neurocognitive development.