Murmurations: a case study in AI-assisted mathematics

We report the emergence of a striking new phenomenon in arithmetic, which we call murmurations. First observed experimentally through averages over large arithmetic datasets, murmurations can be detected and analyzed using standard interpretability tools from machine learning, including principal component weightings, saliency curves, and convolutional filters. Although discovered computationally, they constitute a genuinely new and intriguing phenomenon in arithmetic that can be formulated and investigated using established tools of number theory. In particular, murmurations encode subtle information about Frobenius traces and naturally belong to the framework of arithmetic statistics. More precisely, murmurations connect to central themes surrounding the conjecture of Birch and Swinnerton-Dyer and perspectives from random matrix theory. In this paper, we present an overview of murmurations, contextualizing them within number theory and AI.

Stochastic Scaling in Loss Functions for Physics-Informed Neural Networks

Differential equations are used in a wide variety of disciplines, describing the complex behavior of the physical world. Analytic solutions to these equations are often difficult to solve for, limiting our current ability to solve complex differential equations and necessitating sophisticated numerical methods to approximate solutions. Trained neural networks act as universal function approximators, able to numerically solve differential equations in a novel way. In this work, methods and applications of neural network algorithms for numerically solving differential equations are explored, with an emphasis on varying loss functions and biological applications. Variations on traditional loss function and training parameters show promise in making neural network-aided solutions more efficient, allowing for the investigation of more complex equations governing biological principles.

Murmurations of elliptic curves

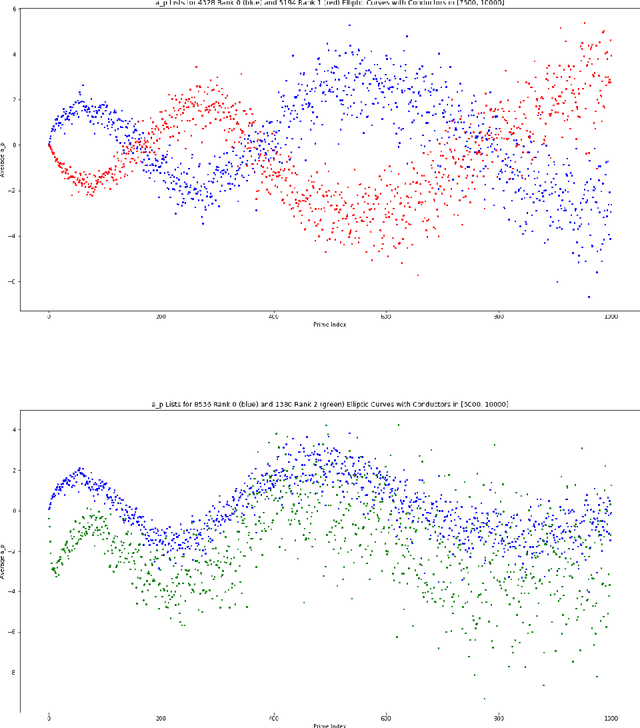
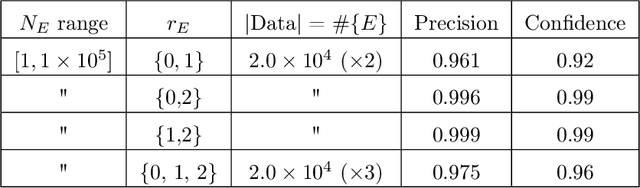
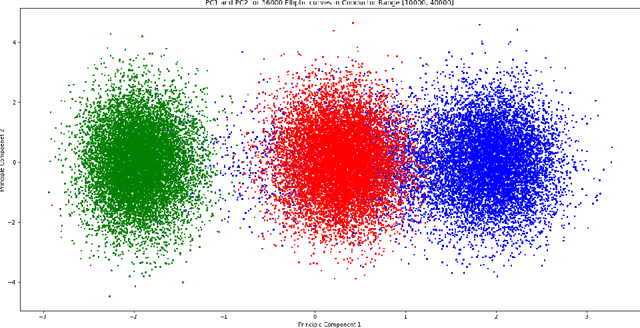
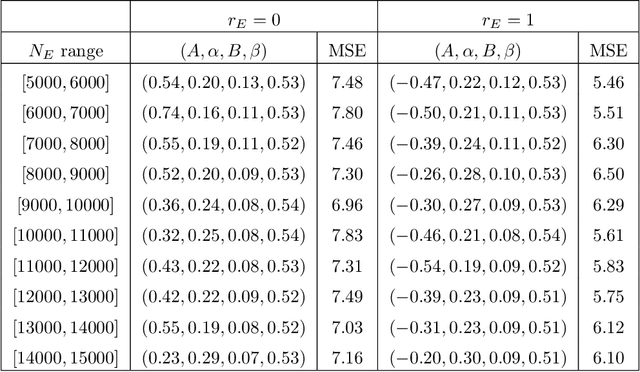
We investigate the average value of the $p$th Dirichlet coefficients of elliptic curves for a prime p in a fixed conductor range with given rank. Plotting this average yields a striking oscillating pattern, the details of which vary with the rank. Based on this observation, we perform various data-scientific experiments with the goal of classifying elliptic curves according to their ranks.