Learning SMaLL Predictors

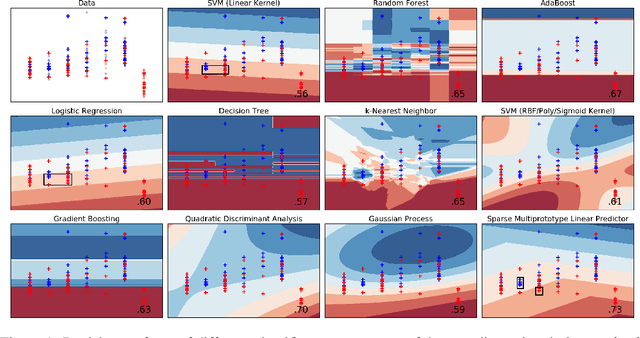
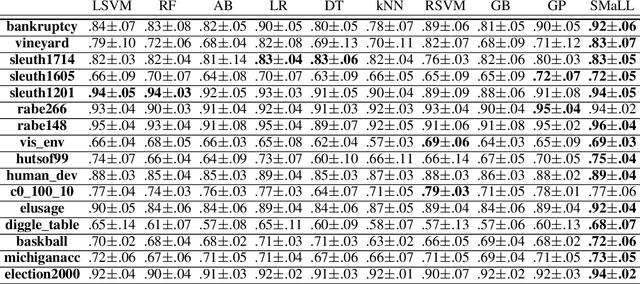
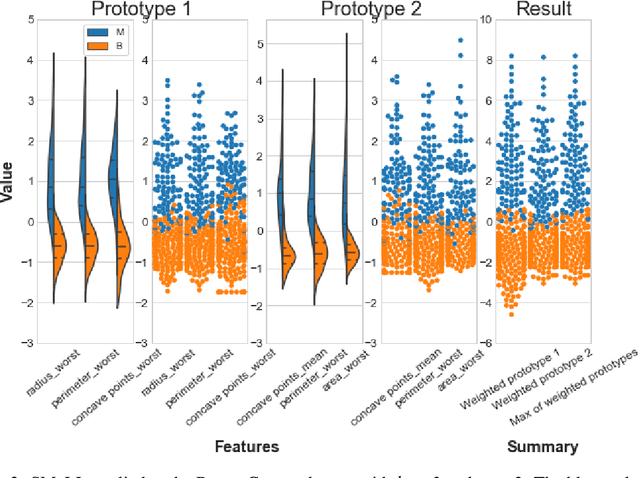
We present a new machine learning technique for training small resource-constrained predictors. Our algorithm, the Sparse Multiprototype Linear Learner (SMaLL), is inspired by the classic machine learning problem of learning $k$-DNF Boolean formulae. We present a formal derivation of our algorithm and demonstrate the benefits of our approach with a detailed empirical study.

Adaptive Neural Networks for Efficient Inference

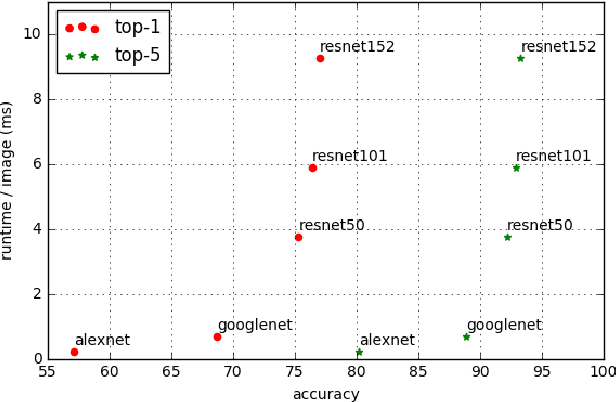
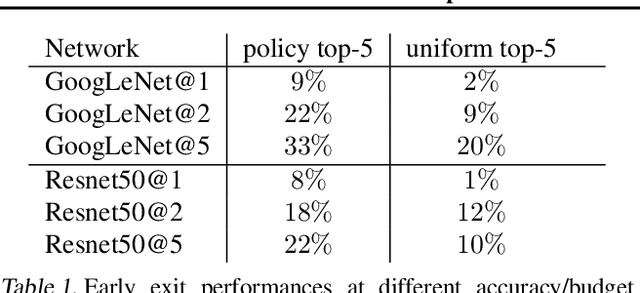
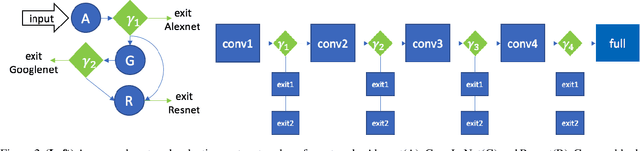
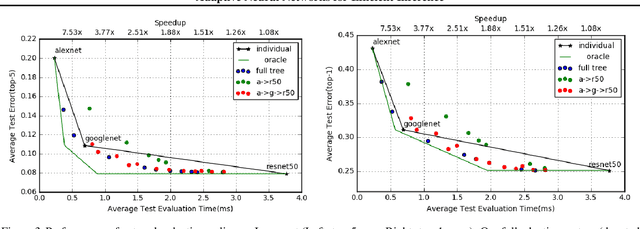
We present an approach to adaptively utilize deep neural networks in order to reduce the evaluation time on new examples without loss of accuracy. Rather than attempting to redesign or approximate existing networks, we propose two schemes that adaptively utilize networks. We first pose an adaptive network evaluation scheme, where we learn a system to adaptively choose the components of a deep network to be evaluated for each example. By allowing examples correctly classified using early layers of the system to exit, we avoid the computational time associated with full evaluation of the network. We extend this to learn a network selection system that adaptively selects the network to be evaluated for each example. We show that computational time can be dramatically reduced by exploiting the fact that many examples can be correctly classified using relatively efficient networks and that complex, computationally costly networks are only necessary for a small fraction of examples. We pose a global objective for learning an adaptive early exit or network selection policy and solve it by reducing the policy learning problem to a layer-by-layer weighted binary classification problem. Empirically, these approaches yield dramatic reductions in computational cost, with up to a 2.8x speedup on state-of-the-art networks from the ImageNet image recognition challenge with minimal (<1%) loss of top5 accuracy.

Linear Learning with Sparse Data

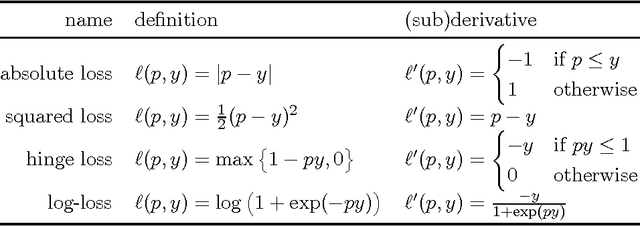
Linear predictors are especially useful when the data is high-dimensional and sparse. One of the standard techniques used to train a linear predictor is the Averaged Stochastic Gradient Descent (ASGD) algorithm. We present an efficient implementation of ASGD that avoids dense vector operations. We also describe a translation invariant extension called Centered Averaged Stochastic Gradient Descent (CASGD).

Online Learning with Feedback Graphs: Beyond Bandits

We study a general class of online learning problems where the feedback is specified by a graph. This class includes online prediction with expert advice and the multi-armed bandit problem, but also several learning problems where the online player does not necessarily observe his own loss. We analyze how the structure of the feedback graph controls the inherent difficulty of the induced $T$-round learning problem. Specifically, we show that any feedback graph belongs to one of three classes: strongly observable graphs, weakly observable graphs, and unobservable graphs. We prove that the first class induces learning problems with $\widetilde\Theta(\alpha^{1/2} T^{1/2})$ minimax regret, where $\alpha$ is the independence number of the underlying graph; the second class induces problems with $\widetilde\Theta(\delta^{1/3}T^{2/3})$ minimax regret, where $\delta$ is the domination number of a certain portion of the graph; and the third class induces problems with linear minimax regret. Our results subsume much of the previous work on learning with feedback graphs and reveal new connections to partial monitoring games. We also show how the regret is affected if the graphs are allowed to vary with time.

Bandit Convex Optimization: sqrt{T} Regret in One Dimension

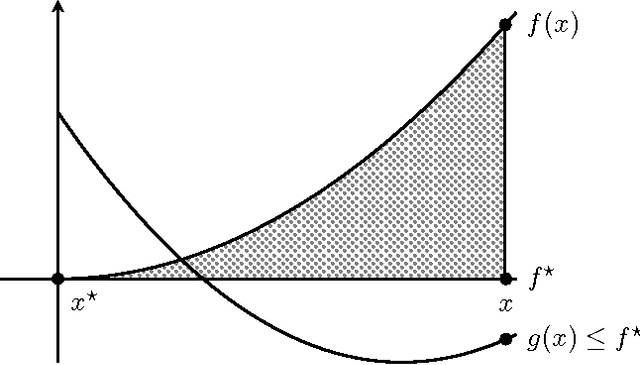
We analyze the minimax regret of the adversarial bandit convex optimization problem. Focusing on the one-dimensional case, we prove that the minimax regret is $\widetilde\Theta(\sqrt{T})$ and partially resolve a decade-old open problem. Our analysis is non-constructive, as we do not present a concrete algorithm that attains this regret rate. Instead, we use minimax duality to reduce the problem to a Bayesian setting, where the convex loss functions are drawn from a worst-case distribution, and then we solve the Bayesian version of the problem with a variant of Thompson Sampling. Our analysis features a novel use of convexity, formalized as a "local-to-global" property of convex functions, that may be of independent interest.

Online Learning with Composite Loss Functions

We study a new class of online learning problems where each of the online algorithm's actions is assigned an adversarial value, and the loss of the algorithm at each step is a known and deterministic function of the values assigned to its recent actions. This class includes problems where the algorithm's loss is the minimum over the recent adversarial values, the maximum over the recent values, or a linear combination of the recent values. We analyze the minimax regret of this class of problems when the algorithm receives bandit feedback, and prove that when the minimum or maximum functions are used, the minimax regret is $\tilde \Omega(T^{2/3})$ (so called hard online learning problems), and when a linear function is used, the minimax regret is $\tilde O(\sqrt{T})$ (so called easy learning problems). Previously, the only online learning problem that was known to be provably hard was the multi-armed bandit with switching costs.

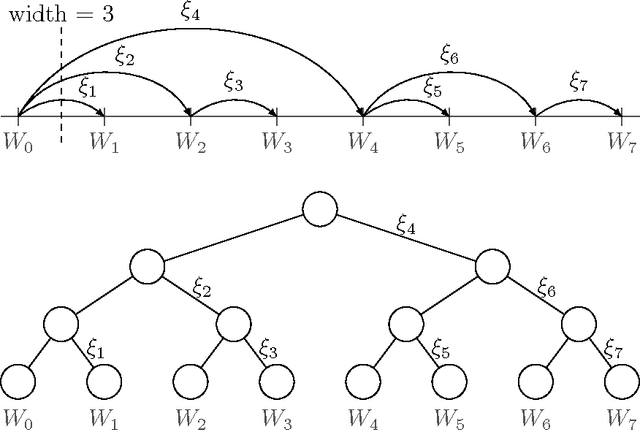
Bandits with Switching Costs: T^{2/3} Regret

We study the adversarial multi-armed bandit problem in a setting where the player incurs a unit cost each time he switches actions. We prove that the player's $T$-round minimax regret in this setting is $\widetilde{\Theta}(T^{2/3})$, thereby closing a fundamental gap in our understanding of learning with bandit feedback. In the corresponding full-information version of the problem, the minimax regret is known to grow at a much slower rate of $\Theta(\sqrt{T})$. The difference between these two rates provides the \emph{first} indication that learning with bandit feedback can be significantly harder than learning with full-information feedback (previous results only showed a different dependence on the number of actions, but not on $T$.) In addition to characterizing the inherent difficulty of the multi-armed bandit problem with switching costs, our results also resolve several other open problems in online learning. One direct implication is that learning with bandit feedback against bounded-memory adaptive adversaries has a minimax regret of $\widetilde{\Theta}(T^{2/3})$. Another implication is that the minimax regret of online learning in adversarial Markov decision processes (MDPs) is $\widetilde{\Theta}(T^{2/3})$. The key to all of our results is a new randomized construction of a multi-scale random walk, which is of independent interest and likely to prove useful in additional settings.

Online Learning with Switching Costs and Other Adaptive Adversaries

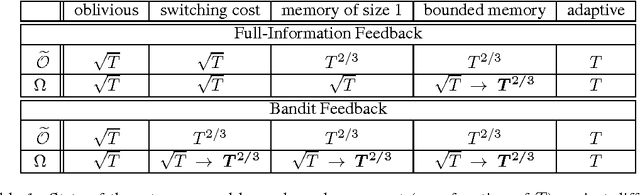
We study the power of different types of adaptive (nonoblivious) adversaries in the setting of prediction with expert advice, under both full-information and bandit feedback. We measure the player's performance using a new notion of regret, also known as policy regret, which better captures the adversary's adaptiveness to the player's behavior. In a setting where losses are allowed to drift, we characterize ---in a nearly complete manner--- the power of adaptive adversaries with bounded memories and switching costs. In particular, we show that with switching costs, the attainable rate with bandit feedback is $\widetilde{\Theta}(T^{2/3})$. Interestingly, this rate is significantly worse than the $\Theta(\sqrt{T})$ rate attainable with switching costs in the full-information case. Via a novel reduction from experts to bandits, we also show that a bounded memory adversary can force $\widetilde{\Theta}(T^{2/3})$ regret even in the full information case, proving that switching costs are easier to control than bounded memory adversaries. Our lower bounds rely on a new stochastic adversary strategy that generates loss processes with strong dependencies.

Deterministic MDPs with Adversarial Rewards and Bandit Feedback

We consider a Markov decision process with deterministic state transition dynamics, adversarially generated rewards that change arbitrarily from round to round, and a bandit feedback model in which the decision maker only observes the rewards it receives. In this setting, we present a novel and efficient online decision making algorithm named MarcoPolo. Under mild assumptions on the structure of the transition dynamics, we prove that MarcoPolo enjoys a regret of O(T^(3/4)sqrt(log(T))) against the best deterministic policy in hindsight. Specifically, our analysis does not rely on the stringent unichain assumption, which dominates much of the previous work on this topic.

Online Bandit Learning against an Adaptive Adversary: from Regret to Policy Regret

Online learning algorithms are designed to learn even when their input is generated by an adversary. The widely-accepted formal definition of an online algorithm's ability to learn is the game-theoretic notion of regret. We argue that the standard definition of regret becomes inadequate if the adversary is allowed to adapt to the online algorithm's actions. We define the alternative notion of policy regret, which attempts to provide a more meaningful way to measure an online algorithm's performance against adaptive adversaries. Focusing on the online bandit setting, we show that no bandit algorithm can guarantee a sublinear policy regret against an adaptive adversary with unbounded memory. On the other hand, if the adversary's memory is bounded, we present a general technique that converts any bandit algorithm with a sublinear regret bound into an algorithm with a sublinear policy regret bound. We extend this result to other variants of regret, such as switching regret, internal regret, and swap regret.