Adaptive maximization of social welfare

We consider the problem of repeatedly choosing policies to maximize social welfare. Welfare is a weighted sum of private utility and public revenue. Earlier outcomes inform later policies. Utility is not observed, but indirectly inferred. Response functions are learned through experimentation. We derive a lower bound on regret, and a matching adversarial upper bound for a variant of the Exp3 algorithm. Cumulative regret grows at a rate of $T^{2/3}$. This implies that (i) welfare maximization is harder than the multi-armed bandit problem (with a rate of $T^{1/2}$ for finite policy sets), and (ii) our algorithm achieves the optimal rate. For the stochastic setting, if social welfare is concave, we can achieve a rate of $T^{1/2}$ (for continuous policy sets), using a dyadic search algorithm. We analyze an extension to nonlinear income taxation, and sketch an extension to commodity taxation. We compare our setting to monopoly pricing (which is easier), and price setting for bilateral trade (which is harder).

Trading-Off Payments and Accuracy in Online Classification with Paid Stochastic Experts

We investigate online classification with paid stochastic experts. Here, before making their prediction, each expert must be paid. The amount that we pay each expert directly influences the accuracy of their prediction through some unknown Lipschitz "productivity" function. In each round, the learner must decide how much to pay each expert and then make a prediction. They incur a cost equal to a weighted sum of the prediction error and upfront payments for all experts. We introduce an online learning algorithm whose total cost after $T$ rounds exceeds that of a predictor which knows the productivity of all experts in advance by at most $\mathcal{O}(K^2(\log T)\sqrt{T})$ where $K$ is the number of experts. In order to achieve this result, we combine Lipschitz bandits and online classification with surrogate losses. These tools allow us to improve upon the bound of order $T^{2/3}$ one would obtain in the standard Lipschitz bandit setting. Our algorithm is empirically evaluated on synthetic data

Efficient Second Order Online Learning by Sketching

We propose Sketched Online Newton (SON), an online second order learning algorithm that enjoys substantially improved regret guarantees for ill-conditioned data. SON is an enhanced version of the Online Newton Step, which, via sketching techniques enjoys a running time linear in the dimension and sketch size. We further develop sparse forms of the sketching methods (such as Oja's rule), making the computation linear in the sparsity of features. Together, the algorithm eliminates all computational obstacles in previous second order online learning approaches.

Online Learning with Switching Costs and Other Adaptive Adversaries

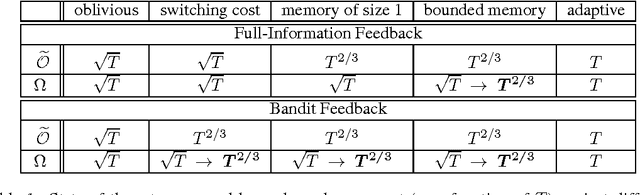
We study the power of different types of adaptive (nonoblivious) adversaries in the setting of prediction with expert advice, under both full-information and bandit feedback. We measure the player's performance using a new notion of regret, also known as policy regret, which better captures the adversary's adaptiveness to the player's behavior. In a setting where losses are allowed to drift, we characterize ---in a nearly complete manner--- the power of adaptive adversaries with bounded memories and switching costs. In particular, we show that with switching costs, the attainable rate with bandit feedback is $\widetilde{\Theta}(T^{2/3})$. Interestingly, this rate is significantly worse than the $\Theta(\sqrt{T})$ rate attainable with switching costs in the full-information case. Via a novel reduction from experts to bandits, we also show that a bounded memory adversary can force $\widetilde{\Theta}(T^{2/3})$ regret even in the full information case, proving that switching costs are easier to control than bounded memory adversaries. Our lower bounds rely on a new stochastic adversary strategy that generates loss processes with strong dependencies.

A Linear Time Active Learning Algorithm for Link Classification -- Full Version --

We present very efficient active learning algorithms for link classification in signed networks. Our algorithms are motivated by a stochastic model in which edge labels are obtained through perturbations of a initial sign assignment consistent with a two-clustering of the nodes. We provide a theoretical analysis within this model, showing that we can achieve an optimal (to whithin a constant factor) number of mistakes on any graph G = (V,E) such that |E| = \Omega(|V|^{3/2}) by querying O(|V|^{3/2}) edge labels. More generally, we show an algorithm that achieves optimality to within a factor of O(k) by querying at most order of |V| + (|V|/k)^{3/2} edge labels. The running time of this algorithm is at most of order |E| + |V|\log|V|.

A Correlation Clustering Approach to Link Classification in Signed Networks -- Full Version --

Motivated by social balance theory, we develop a theory of link classification in signed networks using the correlation clustering index as measure of label regularity. We derive learning bounds in terms of correlation clustering within three fundamental transductive learning settings: online, batch and active. Our main algorithmic contribution is in the active setting, where we introduce a new family of efficient link classifiers based on covering the input graph with small circuits. These are the first active algorithms for link classification with mistake bounds that hold for arbitrary signed networks.

See the Tree Through the Lines: The Shazoo Algorithm -- Full Version --

Predicting the nodes of a given graph is a fascinating theoretical problem with applications in several domains. Since graph sparsification via spanning trees retains enough information while making the task much easier, trees are an important special case of this problem. Although it is known how to predict the nodes of an unweighted tree in a nearly optimal way, in the weighted case a fully satisfactory algorithm is not available yet. We fill this hole and introduce an efficient node predictor, Shazoo, which is nearly optimal on any weighted tree. Moreover, we show that Shazoo can be viewed as a common nontrivial generalization of both previous approaches for unweighted trees and weighted lines. Experiments on real-world datasets confirm that Shazoo performs well in that it fully exploits the structure of the input tree, and gets very close to (and sometimes better than) less scalable energy minimization methods.

Active Learning on Trees and Graphs

We investigate the problem of active learning on a given tree whose nodes are assigned binary labels in an adversarial way. Inspired by recent results by Guillory and Bilmes, we characterize (up to constant factors) the optimal placement of queries so to minimize the mistakes made on the non-queried nodes. Our query selection algorithm is extremely efficient, and the optimal number of mistakes on the non-queried nodes is achieved by a simple and efficient mincut classifier. Through a simple modification of the query selection algorithm we also show optimality (up to constant factors) with respect to the trade-off between number of queries and number of mistakes on non-queried nodes. By using spanning trees, our algorithms can be efficiently applied to general graphs, although the problem of finding optimal and efficient active learning algorithms for general graphs remains open. Towards this end, we provide a lower bound on the number of mistakes made on arbitrary graphs by any active learning algorithm using a number of queries which is up to a constant fraction of the graph size.