Gilad Yehudai
Querying Kernel Methods Suffices for Reconstructing their Training Data
May 25, 2025
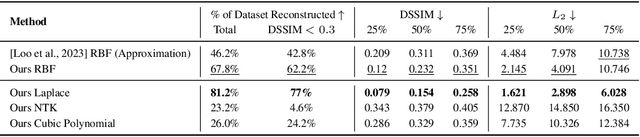
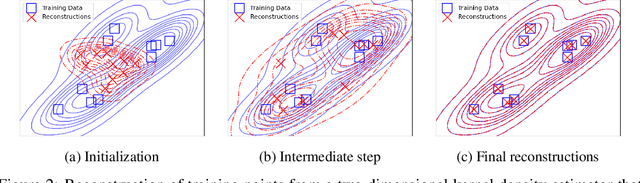
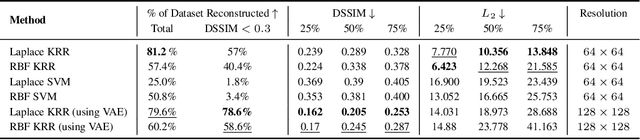
Abstract:Over-parameterized models have raised concerns about their potential to memorize training data, even when achieving strong generalization. The privacy implications of such memorization are generally unclear, particularly in scenarios where only model outputs are accessible. We study this question in the context of kernel methods, and demonstrate both empirically and theoretically that querying kernel models at various points suffices to reconstruct their training data, even without access to model parameters. Our results hold for a range of kernel methods, including kernel regression, support vector machines, and kernel density estimation. Our hope is that this work can illuminate potential privacy concerns for such models.
Compositional Reasoning with Transformers, RNNs, and Chain of Thought
Mar 03, 2025
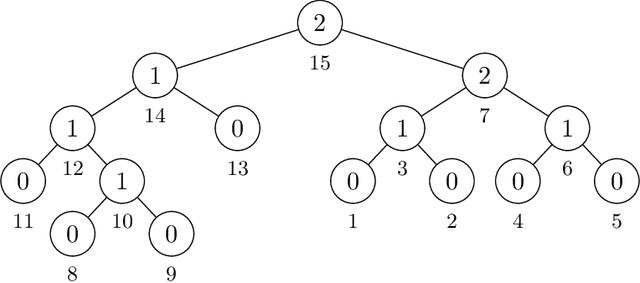
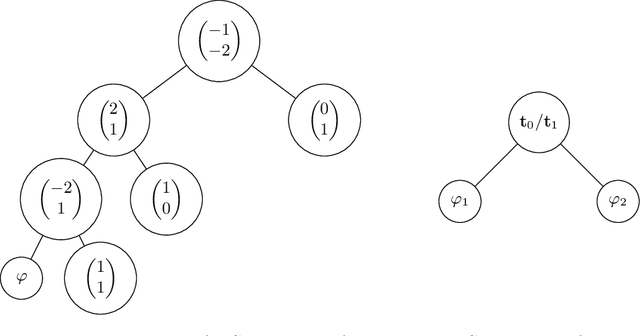
Abstract:We study and compare the expressive power of transformers, RNNs, and transformers with chain of thought tokens on a simple and natural class of problems we term Compositional Reasoning Questions (CRQ). This family captures problems like evaluating Boolean formulas and multi-step word problems. Assuming standard hardness assumptions from circuit complexity and communication complexity, we prove that none of these three architectures is capable of solving CRQs unless some hyperparameter (depth, embedding dimension, and number of chain of thought tokens, respectively) grows with the size of the input. We also provide a construction for each architecture that solves CRQs. For transformers, our construction uses depth that is logarithmic in the problem size. For RNNs, logarithmic embedding dimension is necessary and sufficient, so long as the inputs are provided in a certain order. (Otherwise, a linear dimension is necessary). For transformers with chain of thought, our construction uses $n$ CoT tokens. These results show that, while CRQs are inherently hard, there are several different ways for language models to overcome this hardness. Even for a single class of problems, each architecture has strengths and weaknesses, and none is strictly better than the others.
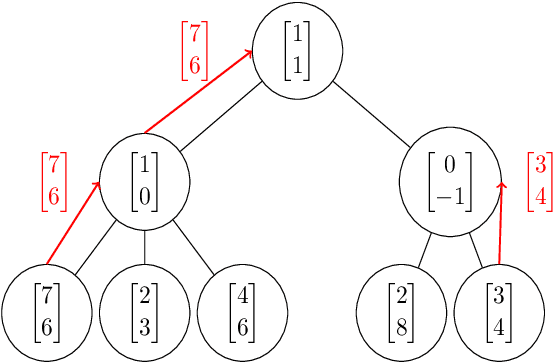
Depth-Width tradeoffs in Algorithmic Reasoning of Graph Tasks with Transformers
Mar 03, 2025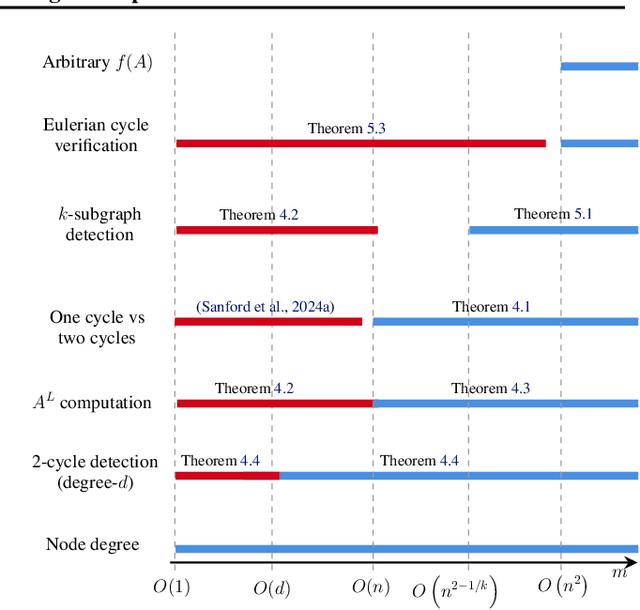
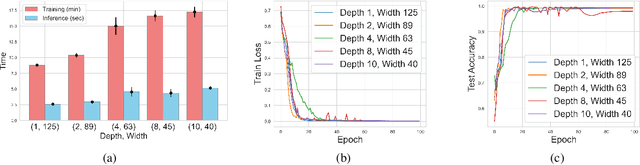

Abstract:Transformers have revolutionized the field of machine learning. In particular, they can be used to solve complex algorithmic problems, including graph-based tasks. In such algorithmic tasks a key question is what is the minimal size of a transformer that can implement a task. Recent work has begun to explore this problem for graph-based tasks, showing that for sub-linear embedding dimension (i.e., model width) logarithmic depth suffices. However, an open question, which we address here, is what happens if width is allowed to grow linearly. Here we analyze this setting, and provide the surprising result that with linear width, constant depth suffices for solving a host of graph-based problems. This suggests that a moderate increase in width can allow much shallower models, which are advantageous in terms of inference time. For other problems, we show that quadratic width is required. Our results demonstrate the complex and intriguing landscape of transformer implementations of graph-based algorithms. We support our theoretical results with empirical evaluations.
On the Reconstruction of Training Data from Group Invariant Networks
Nov 25, 2024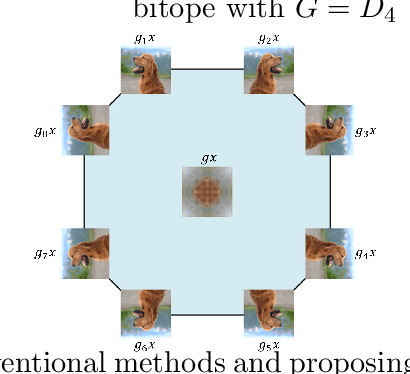


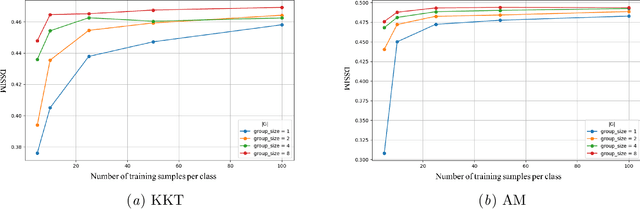
Abstract:Reconstructing training data from trained neural networks is an active area of research with significant implications for privacy and explainability. Recent advances have demonstrated the feasibility of this process for several data types. However, reconstructing data from group-invariant neural networks poses distinct challenges that remain largely unexplored. This paper addresses this gap by first formulating the problem and discussing some of its basic properties. We then provide an experimental evaluation demonstrating that conventional reconstruction techniques are inadequate in this scenario. Specifically, we observe that the resulting data reconstructions gravitate toward symmetric inputs on which the group acts trivially, leading to poor-quality results. Finally, we propose two novel methods aiming to improve reconstruction in this setup and present promising preliminary experimental results. Our work sheds light on the complexities of reconstructing data from group invariant neural networks and offers potential avenues for future research in this domain.
On the Benefits of Rank in Attention Layers
Jul 23, 2024



Abstract:Attention-based mechanisms are widely used in machine learning, most prominently in transformers. However, hyperparameters such as the rank of the attention matrices and the number of heads are scaled nearly the same way in all realizations of this architecture, without theoretical justification. In this work we show that there are dramatic trade-offs between the rank and number of heads of the attention mechanism. Specifically, we present a simple and natural target function that can be represented using a single full-rank attention head for any context length, but that cannot be approximated by low-rank attention unless the number of heads is exponential in the embedding dimension, even for short context lengths. Moreover, we prove that, for short context lengths, adding depth allows the target to be approximated by low-rank attention. For long contexts, we conjecture that full-rank attention is necessary. Finally, we present experiments with off-the-shelf transformers that validate our theoretical findings.
Reconstructing Training Data From Real World Models Trained with Transfer Learning
Jul 22, 2024Abstract:Current methods for reconstructing training data from trained classifiers are restricted to very small models, limited training set sizes, and low-resolution images. Such restrictions hinder their applicability to real-world scenarios. In this paper, we present a novel approach enabling data reconstruction in realistic settings for models trained on high-resolution images. Our method adapts the reconstruction scheme of arXiv:2206.07758 to real-world scenarios -- specifically, targeting models trained via transfer learning over image embeddings of large pre-trained models like DINO-ViT and CLIP. Our work employs data reconstruction in the embedding space rather than in the image space, showcasing its applicability beyond visual data. Moreover, we introduce a novel clustering-based method to identify good reconstructions from thousands of candidates. This significantly improves on previous works that relied on knowledge of the training set to identify good reconstructed images. Our findings shed light on a potential privacy risk for data leakage from models trained using transfer learning.
When Can Transformers Count to n?
Jul 21, 2024Abstract:Large language models based on the transformer architectures can solve highly complex tasks. But are there simple tasks that such models cannot solve? Here we focus on very simple counting tasks, that involve counting how many times a token in the vocabulary have appeared in a string. We show that if the dimension of the transformer state is linear in the context length, this task can be solved. However, the solution we propose does not scale beyond this limit, and we provide theoretical arguments for why it is likely impossible for a size limited transformer to implement this task. Our empirical results demonstrate the same phase-transition in performance, as anticipated by the theoretical argument. Our results demonstrate the importance of understanding how transformers can solve simple tasks.
MALT Powers Up Adversarial Attacks
Jul 02, 2024

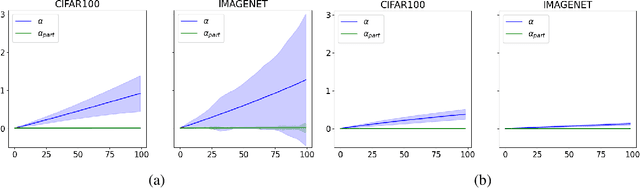
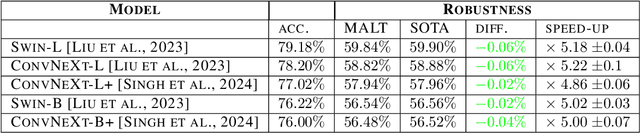
Abstract:Current adversarial attacks for multi-class classifiers choose the target class for a given input naively, based on the classifier's confidence levels for various target classes. We present a novel adversarial targeting method, \textit{MALT - Mesoscopic Almost Linearity Targeting}, based on medium-scale almost linearity assumptions. Our attack wins over the current state of the art AutoAttack on the standard benchmark datasets CIFAR-100 and ImageNet and for a variety of robust models. In particular, our attack is \emph{five times faster} than AutoAttack, while successfully matching all of AutoAttack's successes and attacking additional samples that were previously out of reach. We then prove formally and demonstrate empirically that our targeting method, although inspired by linear predictors, also applies to standard non-linear models.
RedEx: Beyond Fixed Representation Methods via Convex Optimization
Jan 15, 2024Abstract:Optimizing Neural networks is a difficult task which is still not well understood. On the other hand, fixed representation methods such as kernels and random features have provable optimization guarantees but inferior performance due to their inherent inability to learn the representations. In this paper, we aim at bridging this gap by presenting a novel architecture called RedEx (Reduced Expander Extractor) that is as expressive as neural networks and can also be trained in a layer-wise fashion via a convex program with semi-definite constraints and optimization guarantees. We also show that RedEx provably surpasses fixed representation methods, in the sense that it can efficiently learn a family of target functions which fixed representation methods cannot.
Locally Optimal Descent for Dynamic Stepsize Scheduling
Nov 23, 2023



Abstract:We introduce a novel dynamic learning-rate scheduling scheme grounded in theory with the goal of simplifying the manual and time-consuming tuning of schedules in practice. Our approach is based on estimating the locally-optimal stepsize, guaranteeing maximal descent in the direction of the stochastic gradient of the current step. We first establish theoretical convergence bounds for our method within the context of smooth non-convex stochastic optimization, matching state-of-the-art bounds while only assuming knowledge of the smoothness parameter. We then present a practical implementation of our algorithm and conduct systematic experiments across diverse datasets and optimization algorithms, comparing our scheme with existing state-of-the-art learning-rate schedulers. Our findings indicate that our method needs minimal tuning when compared to existing approaches, removing the need for auxiliary manual schedules and warm-up phases and achieving comparable performance with drastically reduced parameter tuning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge