Querying Kernel Methods Suffices for Reconstructing their Training Data

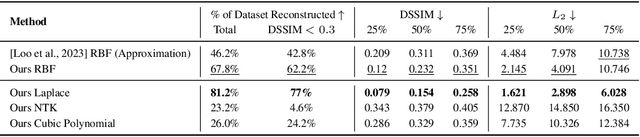
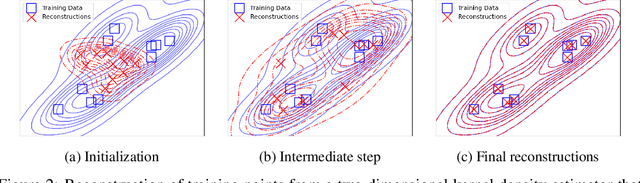
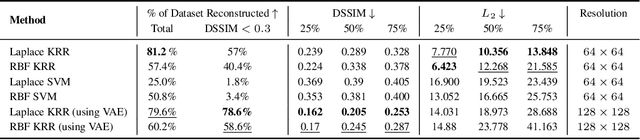
Over-parameterized models have raised concerns about their potential to memorize training data, even when achieving strong generalization. The privacy implications of such memorization are generally unclear, particularly in scenarios where only model outputs are accessible. We study this question in the context of kernel methods, and demonstrate both empirically and theoretically that querying kernel models at various points suffices to reconstruct their training data, even without access to model parameters. Our results hold for a range of kernel methods, including kernel regression, support vector machines, and kernel density estimation. Our hope is that this work can illuminate potential privacy concerns for such models.

When Models Don't Collapse: On the Consistency of Iterative MLE

The widespread use of generative models has created a feedback loop, in which each generation of models is trained on data partially produced by its predecessors. This process has raised concerns about \emph{model collapse}: A critical degradation in performance caused by repeated training on synthetic data. However, different analyses in the literature have reached different conclusions as to the severity of model collapse. As such, it remains unclear how concerning this phenomenon is, and under which assumptions it can be avoided. To address this, we theoretically study model collapse for maximum likelihood estimation (MLE), in a natural setting where synthetic data is gradually added to the original data set. Under standard assumptions (similar to those long used for proving asymptotic consistency and normality of MLE), we establish non-asymptotic bounds showing that collapse can be avoided even as the fraction of real data vanishes. On the other hand, we prove that some assumptions (beyond MLE consistency) are indeed necessary: Without them, model collapse can occur arbitrarily quickly, even when the original data is still present in the training set. To the best of our knowledge, these are the first rigorous examples of iterative generative modeling with accumulating data that rapidly leads to model collapse.

Overfitting Regimes of Nadaraya-Watson Interpolators

In recent years, there has been much interest in understanding the generalization behavior of interpolating predictors, which overfit on noisy training data. Whereas standard analyses are concerned with whether a method is consistent or not, recent observations have shown that even inconsistent predictors can generalize well. In this work, we revisit the classic interpolating Nadaraya-Watson (NW) estimator (also known as Shepard's method), and study its generalization capabilities through this modern viewpoint. In particular, by varying a single bandwidth-like hyperparameter, we prove the existence of multiple overfitting behaviors, ranging non-monotonically from catastrophic, through benign, to tempered. Our results highlight how even classical interpolating methods can exhibit intricate generalization behaviors. Numerical experiments complement our theory, demonstrating the same phenomena.

Simple Relative Deviation Bounds for Covariance and Gram Matrices

We provide non-asymptotic, relative deviation bounds for the eigenvalues of empirical covariance and gram matrices in general settings. Unlike typical uniform bounds, which may fail to capture the behavior of smaller eigenvalues, our results provide sharper control across the spectrum. Our analysis is based on a general-purpose theorem that allows one to convert existing uniform bounds into relative ones. The theorems and techniques emphasize simplicity and should be applicable across various settings.

Generalization in Kernel Regression Under Realistic Assumptions

It is by now well-established that modern over-parameterized models seem to elude the bias-variance tradeoff and generalize well despite overfitting noise. Many recent works attempt to analyze this phenomenon in the relatively tractable setting of kernel regression. However, as we argue in detail, most past works on this topic either make unrealistic assumptions, or focus on a narrow problem setup. This work aims to provide a unified theory to upper bound the excess risk of kernel regression for nearly all common and realistic settings. Specifically, we provide rigorous bounds that hold for common kernels and for any amount of regularization, noise, any input dimension, and any number of samples. Furthermore, we provide relative perturbation bounds for the eigenvalues of kernel matrices, which may be of independent interest. These reveal a self-regularization phenomenon, whereby a heavy tail in the eigendecomposition of the kernel provides it with an implicit form of regularization, enabling good generalization. When applied to common kernels, our results imply benign overfitting in high input dimensions, nearly tempered overfitting in fixed dimensions, and explicit convergence rates for regularized regression. As a by-product, we obtain time-dependent bounds for neural networks trained in the kernel regime.

Controlling the Inductive Bias of Wide Neural Networks by Modifying the Kernel's Spectrum

Wide neural networks are biased towards learning certain functions, influencing both the rate of convergence of gradient descent (GD) and the functions that are reachable with GD in finite training time. As such, there is a great need for methods that can modify this bias according to the task at hand. To that end, we introduce Modified Spectrum Kernels (MSKs), a novel family of constructed kernels that can be used to approximate kernels with desired eigenvalues for which no closed form is known. We leverage the duality between wide neural networks and Neural Tangent Kernels and propose a preconditioned gradient descent method, which alters the trajectory of GD. As a result, this allows for a polynomial and, in some cases, exponential training speedup without changing the final solution. Our method is both computationally efficient and simple to implement.

A Kernel Perspective of Skip Connections in Convolutional Networks

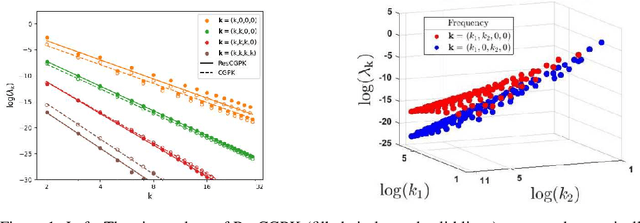
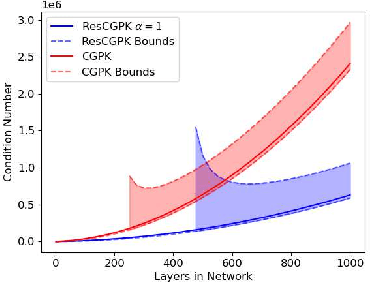
Over-parameterized residual networks (ResNets) are amongst the most successful convolutional neural architectures for image processing. Here we study their properties through their Gaussian Process and Neural Tangent kernels. We derive explicit formulas for these kernels, analyze their spectra, and provide bounds on their implied condition numbers. Our results indicate that (1) with ReLU activation, the eigenvalues of these residual kernels decay polynomially at a similar rate compared to the same kernels when skip connections are not used, thus maintaining a similar frequency bias; (2) however, residual kernels are more locally biased. Our analysis further shows that the matrices obtained by these residual kernels yield favorable condition numbers at finite depths than those obtained without the skip connections, enabling therefore faster convergence of training with gradient descent.