GSVisLoc: Generalizable Visual Localization for Gaussian Splatting Scene Representations

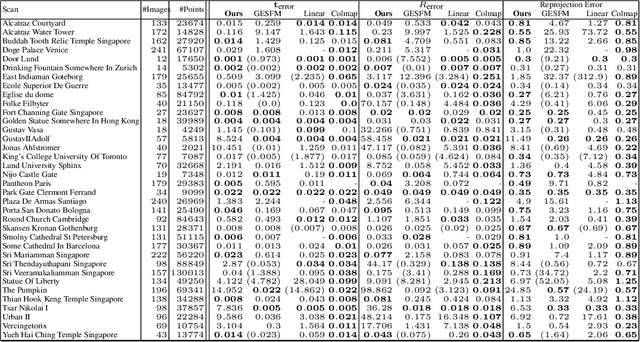
We introduce GSVisLoc, a visual localization method designed for 3D Gaussian Splatting (3DGS) scene representations. Given a 3DGS model of a scene and a query image, our goal is to estimate the camera's position and orientation. We accomplish this by robustly matching scene features to image features. Scene features are produced by downsampling and encoding the 3D Gaussians while image features are obtained by encoding image patches. Our algorithm proceeds in three steps, starting with coarse matching, then fine matching, and finally by applying pose refinement for an accurate final estimate. Importantly, our method leverages the explicit 3DGS scene representation for visual localization without requiring modifications, retraining, or additional reference images. We evaluate GSVisLoc on both indoor and outdoor scenes, demonstrating competitive localization performance on standard benchmarks while outperforming existing 3DGS-based baselines. Moreover, our approach generalizes effectively to novel scenes without additional training.

Querying Kernel Methods Suffices for Reconstructing their Training Data

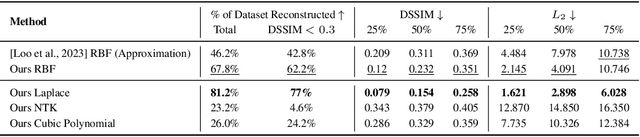
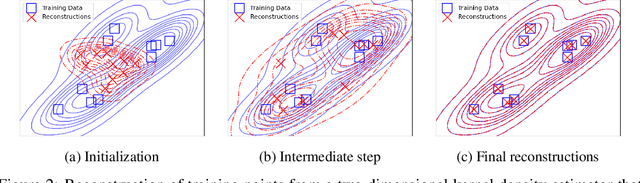
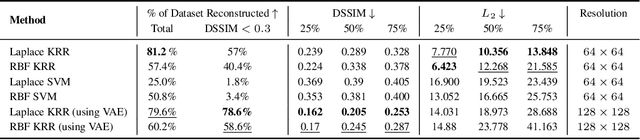
Over-parameterized models have raised concerns about their potential to memorize training data, even when achieving strong generalization. The privacy implications of such memorization are generally unclear, particularly in scenarios where only model outputs are accessible. We study this question in the context of kernel methods, and demonstrate both empirically and theoretically that querying kernel models at various points suffices to reconstruct their training data, even without access to model parameters. Our results hold for a range of kernel methods, including kernel regression, support vector machines, and kernel density estimation. Our hope is that this work can illuminate potential privacy concerns for such models.

On the Reconstruction of Training Data from Group Invariant Networks

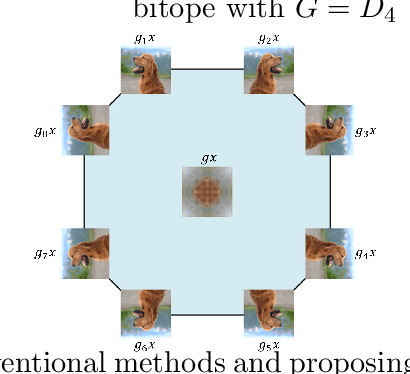
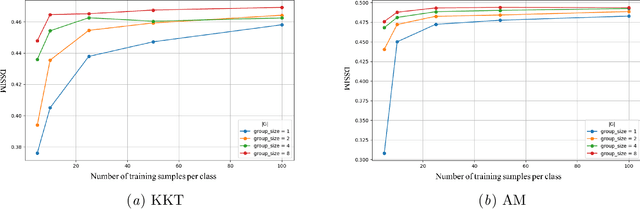
Reconstructing training data from trained neural networks is an active area of research with significant implications for privacy and explainability. Recent advances have demonstrated the feasibility of this process for several data types. However, reconstructing data from group-invariant neural networks poses distinct challenges that remain largely unexplored. This paper addresses this gap by first formulating the problem and discussing some of its basic properties. We then provide an experimental evaluation demonstrating that conventional reconstruction techniques are inadequate in this scenario. Specifically, we observe that the resulting data reconstructions gravitate toward symmetric inputs on which the group acts trivially, leading to poor-quality results. Finally, we propose two novel methods aiming to improve reconstruction in this setup and present promising preliminary experimental results. Our work sheds light on the complexities of reconstructing data from group invariant neural networks and offers potential avenues for future research in this domain.

Consensus Learning with Deep Sets for Essential Matrix Estimation

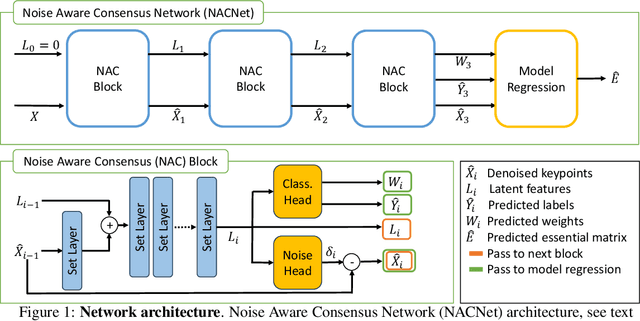
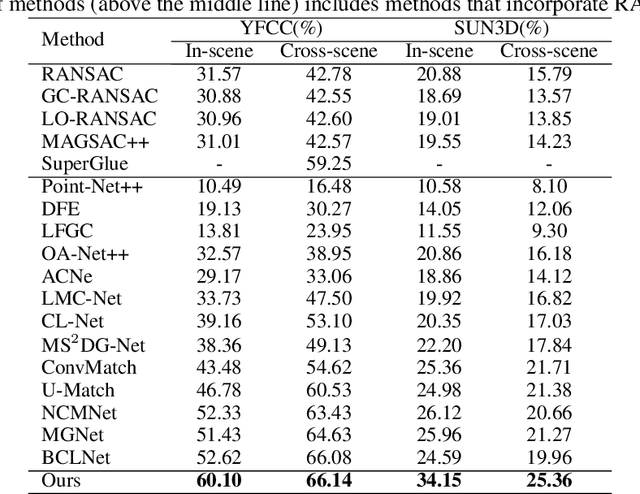
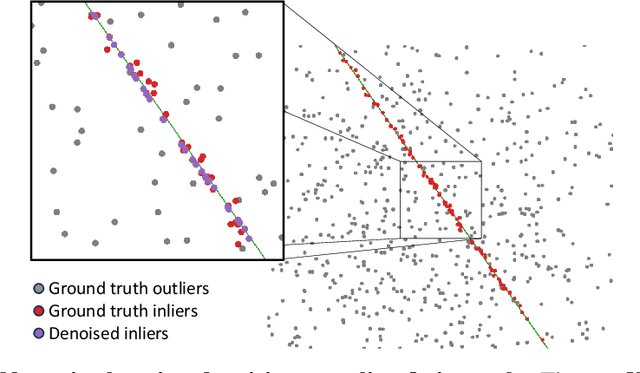
Robust estimation of the essential matrix, which encodes the relative position and orientation of two cameras, is a fundamental step in structure from motion pipelines. Recent deep-based methods achieved accurate estimation by using complex network architectures that involve graphs, attention layers, and hard pruning steps. Here, we propose a simpler network architecture based on Deep Sets. Given a collection of point matches extracted from two images, our method identifies outlier point matches and models the displacement noise in inlier matches. A weighted DLT module uses these predictions to regress the essential matrix. Our network achieves accurate recovery that is superior to existing networks with significantly more complex architectures.

RESFM: Robust Equivariant Multiview Structure from Motion

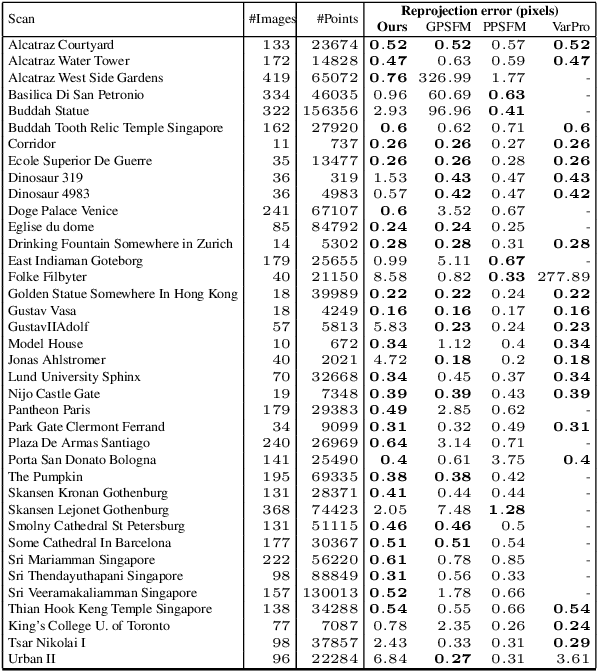
Multiview Structure from Motion is a fundamental and challenging computer vision problem. A recent deep-based approach was proposed utilizing matrix equivariant architectures for the simultaneous recovery of camera pose and 3D scene structure from large image collections. This work however made the unrealistic assumption that the point tracks given as input are clean of outliers. Here we propose an architecture suited to dealing with outliers by adding an inlier/outlier classifying module that respects the model equivariance and by adding a robust bundle adjustment step. Experiments demonstrate that our method can be successfully applied in realistic settings that include large image collections and point tracks extracted with common heuristics and include many outliers.

Controlling the Inductive Bias of Wide Neural Networks by Modifying the Kernel's Spectrum

Wide neural networks are biased towards learning certain functions, influencing both the rate of convergence of gradient descent (GD) and the functions that are reachable with GD in finite training time. As such, there is a great need for methods that can modify this bias according to the task at hand. To that end, we introduce Modified Spectrum Kernels (MSKs), a novel family of constructed kernels that can be used to approximate kernels with desired eigenvalues for which no closed form is known. We leverage the duality between wide neural networks and Neural Tangent Kernels and propose a preconditioned gradient descent method, which alters the trajectory of GD. As a result, this allows for a polynomial and, in some cases, exponential training speedup without changing the final solution. Our method is both computationally efficient and simple to implement.

GRelPose: Generalizable End-to-End Relative Camera Pose Regression

This paper proposes a generalizable, end-to-end deep learning-based method for relative pose regression between two images. Given two images of the same scene captured from different viewpoints, our algorithm predicts the relative rotation and translation between the two respective cameras. Despite recent progress in the field, current deep-based methods exhibit only limited generalization to scenes not seen in training. Our approach introduces a network architecture that extracts a grid of coarse features for each input image using the pre-trained LoFTR network. It subsequently relates corresponding features in the two images, and finally uses a convolutional network to recover the relative rotation and translation between the respective cameras. Our experiments indicate that the proposed architecture can generalize to novel scenes, obtaining higher accuracy than existing deep-learning-based methods in various settings and datasets, in particular with limited training data.

A Kernel Perspective of Skip Connections in Convolutional Networks

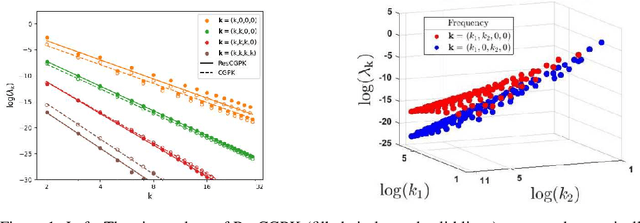
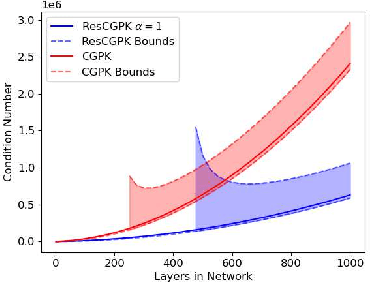
Over-parameterized residual networks (ResNets) are amongst the most successful convolutional neural architectures for image processing. Here we study their properties through their Gaussian Process and Neural Tangent kernels. We derive explicit formulas for these kernels, analyze their spectra, and provide bounds on their implied condition numbers. Our results indicate that (1) with ReLU activation, the eigenvalues of these residual kernels decay polynomially at a similar rate compared to the same kernels when skip connections are not used, thus maintaining a similar frequency bias; (2) however, residual kernels are more locally biased. Our analysis further shows that the matrices obtained by these residual kernels yield favorable condition numbers at finite depths than those obtained without the skip connections, enabling therefore faster convergence of training with gradient descent.

On the Spectral Bias of Convolutional Neural Tangent and Gaussian Process Kernels

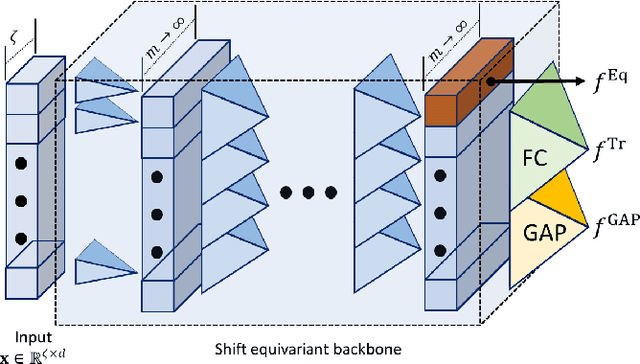
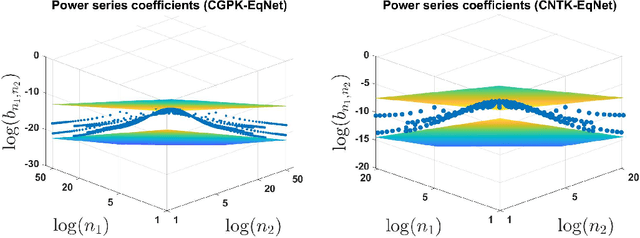
We study the properties of various over-parametrized convolutional neural architectures through their respective Gaussian process and neural tangent kernels. We prove that, with normalized multi-channel input and ReLU activation, the eigenfunctions of these kernels with the uniform measure are formed by products of spherical harmonics, defined over the channels of the different pixels. We next use hierarchical factorizable kernels to bound their respective eigenvalues. We show that the eigenvalues decay polynomially, quantify the rate of decay, and derive measures that reflect the composition of hierarchical features in these networks. Our results provide concrete quantitative characterization of over-parameterized convolutional network architectures.

Deep Permutation Equivariant Structure from Motion

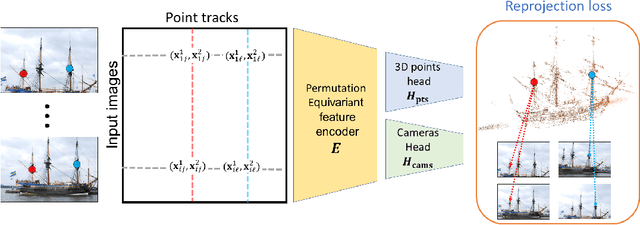
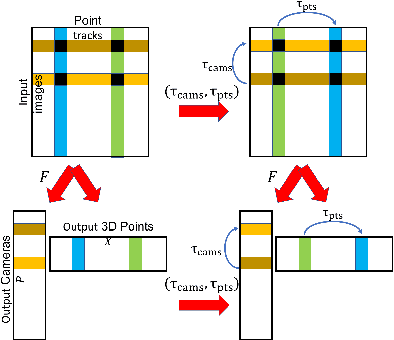
Existing deep methods produce highly accurate 3D reconstructions in stereo and multiview stereo settings, i.e., when cameras are both internally and externally calibrated. Nevertheless, the challenge of simultaneous recovery of camera poses and 3D scene structure in multiview settings with deep networks is still outstanding. Inspired by projective factorization for Structure from Motion (SFM) and by deep matrix completion techniques, we propose a neural network architecture that, given a set of point tracks in multiple images of a static scene, recovers both the camera parameters and a (sparse) scene structure by minimizing an unsupervised reprojection loss. Our network architecture is designed to respect the structure of the problem: the sought output is equivariant to permutations of both cameras and scene points. Notably, our method does not require initialization of camera parameters or 3D point locations. We test our architecture in two setups: (1) single scene reconstruction and (2) learning from multiple scenes. Our experiments, conducted on a variety of datasets in both internally calibrated and uncalibrated settings, indicate that our method accurately recovers pose and structure, on par with classical state of the art methods. Additionally, we show that a pre-trained network can be used to reconstruct novel scenes using inexpensive fine-tuning with no loss of accuracy.