Puzzle: Distillation-Based NAS for Inference-Optimized LLMs

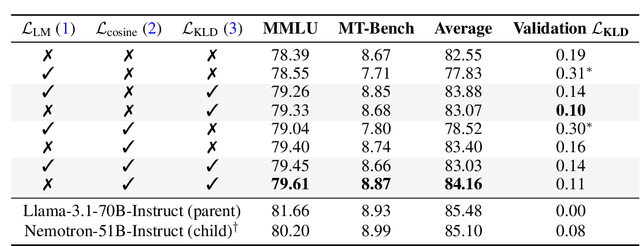
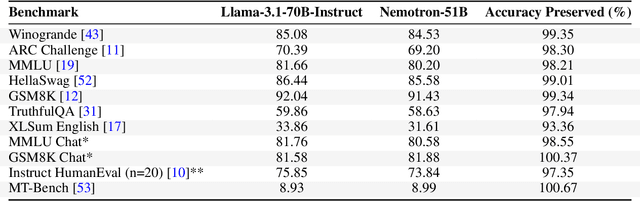
Large language models (LLMs) have demonstrated remarkable capabilities, but their adoption is limited by high computational costs during inference. While increasing parameter counts enhances accuracy, it also widens the gap between state-of-the-art capabilities and practical deployability. We present Puzzle, a framework to accelerate LLM inference on specific hardware while preserving their capabilities. Through an innovative application of neural architecture search (NAS) at an unprecedented scale, Puzzle systematically optimizes models with tens of billions of parameters under hardware constraints. Our approach utilizes blockwise local knowledge distillation (BLD) for parallel architecture exploration and employs mixed-integer programming for precise constraint optimization. We demonstrate the real-world impact of our framework through Llama-3.1-Nemotron-51B-Instruct (Nemotron-51B), a publicly available model derived from Llama-3.1-70B-Instruct. Nemotron-51B achieves a 2.17x inference throughput speedup, fitting on a single NVIDIA H100 GPU while preserving 98.4% of the original model's capabilities. Nemotron-51B currently stands as the most accurate language model capable of inference on a single GPU with large batch sizes. Remarkably, this transformation required just 45B training tokens, compared to over 15T tokens used for the 70B model it was derived from. This establishes a new paradigm where powerful models can be optimized for efficient deployment with only negligible compromise of their capabilities, demonstrating that inference performance, not parameter count alone, should guide model selection. With the release of Nemotron-51B and the presentation of the Puzzle framework, we provide practitioners immediate access to state-of-the-art language modeling capabilities at significantly reduced computational costs.

Controlling the Inductive Bias of Wide Neural Networks by Modifying the Kernel's Spectrum

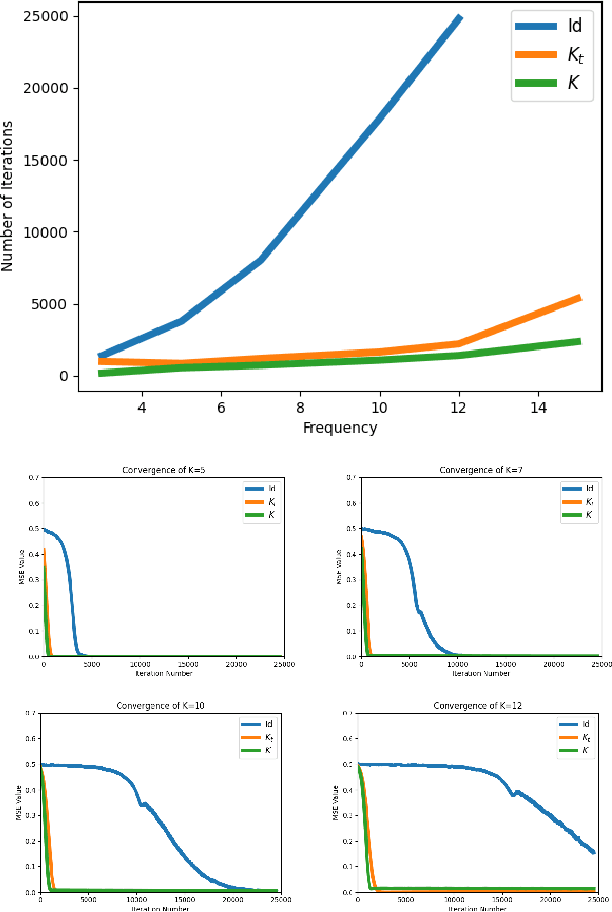
Wide neural networks are biased towards learning certain functions, influencing both the rate of convergence of gradient descent (GD) and the functions that are reachable with GD in finite training time. As such, there is a great need for methods that can modify this bias according to the task at hand. To that end, we introduce Modified Spectrum Kernels (MSKs), a novel family of constructed kernels that can be used to approximate kernels with desired eigenvalues for which no closed form is known. We leverage the duality between wide neural networks and Neural Tangent Kernels and propose a preconditioned gradient descent method, which alters the trajectory of GD. As a result, this allows for a polynomial and, in some cases, exponential training speedup without changing the final solution. Our method is both computationally efficient and simple to implement.

A Kernel Perspective of Skip Connections in Convolutional Networks

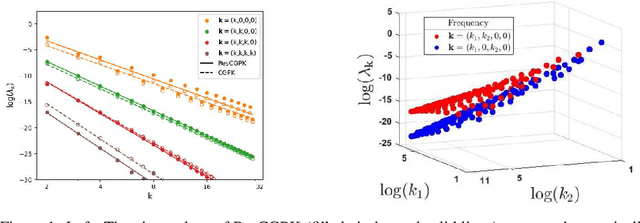
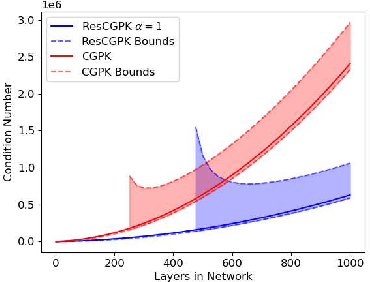
Over-parameterized residual networks (ResNets) are amongst the most successful convolutional neural architectures for image processing. Here we study their properties through their Gaussian Process and Neural Tangent kernels. We derive explicit formulas for these kernels, analyze their spectra, and provide bounds on their implied condition numbers. Our results indicate that (1) with ReLU activation, the eigenvalues of these residual kernels decay polynomially at a similar rate compared to the same kernels when skip connections are not used, thus maintaining a similar frequency bias; (2) however, residual kernels are more locally biased. Our analysis further shows that the matrices obtained by these residual kernels yield favorable condition numbers at finite depths than those obtained without the skip connections, enabling therefore faster convergence of training with gradient descent.

On the Spectral Bias of Convolutional Neural Tangent and Gaussian Process Kernels

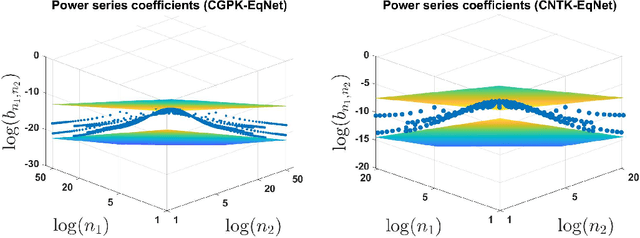
We study the properties of various over-parametrized convolutional neural architectures through their respective Gaussian process and neural tangent kernels. We prove that, with normalized multi-channel input and ReLU activation, the eigenfunctions of these kernels with the uniform measure are formed by products of spherical harmonics, defined over the channels of the different pixels. We next use hierarchical factorizable kernels to bound their respective eigenvalues. We show that the eigenvalues decay polynomially, quantify the rate of decay, and derive measures that reflect the composition of hierarchical features in these networks. Our results provide concrete quantitative characterization of over-parameterized convolutional network architectures.

Spectral Analysis of the Neural Tangent Kernel for Deep Residual Networks

Deep residual network architectures have been shown to achieve superior accuracy over classical feed-forward networks, yet their success is still not fully understood. Focusing on massively over-parameterized, fully connected residual networks with ReLU activation through their respective neural tangent kernels (ResNTK), we provide here a spectral analysis of these kernels. Specifically, we show that, much like NTK for fully connected networks (FC-NTK), for input distributed uniformly on the hypersphere $\mathbb{S}^{d-1}$, the eigenfunctions of ResNTK are the spherical harmonics and the eigenvalues decay polynomially with frequency $k$ as $k^{-d}$. These in turn imply that the set of functions in their Reproducing Kernel Hilbert Space are identical to those of FC-NTK, and consequently also to those of the Laplace kernel. We further show, by drawing on the analogy to the Laplace kernel, that depending on the choice of a hyper-parameter that balances between the skip and residual connections ResNTK can either become spiky with depth, as with FC-NTK, or maintain a stable shape.

On the Similarity between the Laplace and Neural Tangent Kernels

Recent theoretical work has shown that massively overparameterized neural networks are equivalent to kernel regressors that use Neural Tangent Kernels(NTK). Experiments show that these kernel methods perform similarly to real neural networks. Here we show that NTK for fully connected networks is closely related to the standard Laplace kernel. We show theoretically that for normalized data on the hypersphere both kernels have the same eigenfunctions and their eigenvalues decay polynomially at the same rate, implying that their Reproducing Kernel Hilbert Spaces (RKHS) include the same sets of functions. This means that both kernels give rise to classes of functions with the same smoothness properties. The two kernels differ for data off the hypersphere, but experiments indicate that when data is properly normalized these differences are not significant. Finally, we provide experiments on real data comparing NTK and the Laplace kernel, along with a larger class of{\gamma}-exponential kernels. We show that these perform almost identically. Our results suggest that much insight about neural networks can be obtained from analysis of the well-known Laplace kernel, which has a simple closed-form.

Frequency Bias in Neural Networks for Input of Non-Uniform Density

Recent works have partly attributed the generalization ability of over-parameterized neural networks to frequency bias -- networks trained with gradient descent on data drawn from a uniform distribution find a low frequency fit before high frequency ones. As realistic training sets are not drawn from a uniform distribution, we here use the Neural Tangent Kernel (NTK) model to explore the effect of variable density on training dynamics. Our results, which combine analytic and empirical observations, show that when learning a pure harmonic function of frequency $\kappa$, convergence at a point $\x \in \Sphere^{d-1}$ occurs in time $O(\kappa^d/p(\x))$ where $p(\x)$ denotes the local density at $\x$. Specifically, for data in $\Sphere^1$ we analytically derive the eigenfunctions of the kernel associated with the NTK for two-layer networks. We further prove convergence results for deep, fully connected networks with respect to the spectral decomposition of the NTK. Our empirical study highlights similarities and differences between deep and shallow networks in this model.

Averaging Essential and Fundamental Matrices in Collinear Camera Settings

Global methods to Structure from Motion have gained popularity in recent years. A significant drawback of global methods is their sensitivity to collinear camera settings. In this paper, we introduce an analysis and algorithms for averaging bifocal tensors (essential or fundamental matrices) when either subsets or all of the camera centers are collinear. We provide a complete spectral characterization of bifocal tensors in collinear scenarios and further propose two averaging algorithms. The first algorithm uses rank constrained minimization to recover camera matrices in fully collinear settings. The second algorithm enriches the set of possibly mixed collinear and non-collinear cameras with additional, "virtual cameras," which are placed in general position, enabling the application of existing averaging methods to the enriched set of bifocal tensors. Our algorithms are shown to achieve state of the art results on various benchmarks that include autonomous car datasets and unordered image collections in both calibrated and unclibrated settings.

Algebraic Characterization of Essential Matrices and Their Averaging in Multiview Settings

Essential matrix averaging, i.e., the task of recovering camera locations and orientations in calibrated, multiview settings, is a first step in global approaches to Euclidean structure from motion. A common approach to essential matrix averaging is to separately solve for camera orientations and subsequently for camera positions. This paper presents a novel approach that solves simultaneously for both camera orientations and positions. We offer a complete characterization of the algebraic conditions that enable a unique Euclidean reconstruction of $n$ cameras from a collection of $(^n_2)$ essential matrices. We next use these conditions to formulate essential matrix averaging as a constrained optimization problem, allowing us to recover a consistent set of essential matrices given a (possibly partial) set of measured essential matrices computed independently for pairs of images. We finally use the recovered essential matrices to determine the global positions and orientations of the $n$ cameras. We test our method on common SfM datasets, demonstrating high accuracy while maintaining efficiency and robustness, compared to existing methods.

GPSfM: Global Projective SFM Using Algebraic Constraints on Multi-View Fundamental Matrices

This paper addresses the problem of recovering projective camera matrices from collections of fundamental matrices in multiview settings. We make two main contributions. First, given ${n \choose 2}$ fundamental matrices computed for $n$ images, we provide a complete algebraic characterization in the form of conditions that are both necessary and sufficient to enabling the recovery of camera matrices. These conditions are based on arranging the fundamental matrices as blocks in a single matrix, called the $n$-view fundamental matrix, and characterizing this matrix in terms of the signs of its eigenvalues and rank structures. Secondly, we propose a concrete algorithm for projective structure-from-motion that utilizes this characterization. Given a complete or partial collection of measured fundamental matrices, our method seeks camera matrices that minimize a global algebraic error for the measured fundamental matrices. In contrast to existing methods, our optimization, without any initialization, produces a consistent set of fundamental matrices that corresponds to a unique set of cameras (up to a choice of projective frame). Our experiments indicate that our method achieves state of the art performance in both accuracy and running time.