Improving Content Recommendation: Knowledge Graph-Based Semantic Contrastive Learning for Diversity and Cold-Start Users

Addressing the challenges related to data sparsity, cold-start problems, and diversity in recommendation systems is both crucial and demanding. Many current solutions leverage knowledge graphs to tackle these issues by combining both item-based and user-item collaborative signals. A common trend in these approaches focuses on improving ranking performance at the cost of escalating model complexity, reducing diversity, and complicating the task. It is essential to provide recommendations that are both personalized and diverse, rather than solely relying on achieving high rank-based performance, such as Click-through Rate, Recall, etc. In this paper, we propose a hybrid multi-task learning approach, training on user-item and item-item interactions. We apply item-based contrastive learning on descriptive text, sampling positive and negative pairs based on item metadata. Our approach allows the model to better understand the relationships between entities within the knowledge graph by utilizing semantic information from text. It leads to more accurate, relevant, and diverse user recommendations and a benefit that extends even to cold-start users who have few interactions with items. We perform extensive experiments on two widely used datasets to validate the effectiveness of our approach. Our findings demonstrate that jointly training user-item interactions and item-based signals using synopsis text is highly effective. Furthermore, our results provide evidence that item-based contrastive learning enhances the quality of entity embeddings, as indicated by metrics such as uniformity and alignment.

On the Similarity between the Laplace and Neural Tangent Kernels

Recent theoretical work has shown that massively overparameterized neural networks are equivalent to kernel regressors that use Neural Tangent Kernels(NTK). Experiments show that these kernel methods perform similarly to real neural networks. Here we show that NTK for fully connected networks is closely related to the standard Laplace kernel. We show theoretically that for normalized data on the hypersphere both kernels have the same eigenfunctions and their eigenvalues decay polynomially at the same rate, implying that their Reproducing Kernel Hilbert Spaces (RKHS) include the same sets of functions. This means that both kernels give rise to classes of functions with the same smoothness properties. The two kernels differ for data off the hypersphere, but experiments indicate that when data is properly normalized these differences are not significant. Finally, we provide experiments on real data comparing NTK and the Laplace kernel, along with a larger class of{\gamma}-exponential kernels. We show that these perform almost identically. Our results suggest that much insight about neural networks can be obtained from analysis of the well-known Laplace kernel, which has a simple closed-form.

Stabilizing Adversarial Nets With Prediction Methods

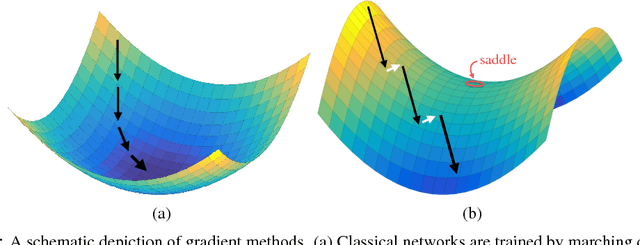
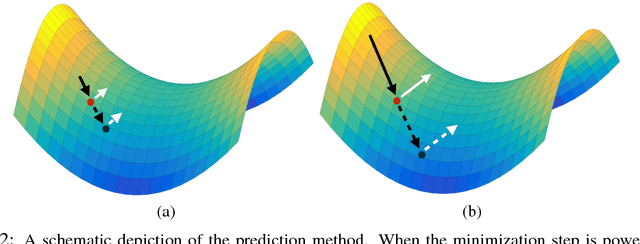
Adversarial neural networks solve many important problems in data science, but are notoriously difficult to train. These difficulties come from the fact that optimal weights for adversarial nets correspond to saddle points, and not minimizers, of the loss function. The alternating stochastic gradient methods typically used for such problems do not reliably converge to saddle points, and when convergence does happen it is often highly sensitive to learning rates. We propose a simple modification of stochastic gradient descent that stabilizes adversarial networks. We show, both in theory and practice, that the proposed method reliably converges to saddle points, and is stable with a wider range of training parameters than a non-prediction method. This makes adversarial networks less likely to "collapse," and enables faster training with larger learning rates.

Big Batch SGD: Automated Inference using Adaptive Batch Sizes

Classical stochastic gradient methods for optimization rely on noisy gradient approximations that become progressively less accurate as iterates approach a solution. The large noise and small signal in the resulting gradients makes it difficult to use them for adaptive stepsize selection and automatic stopping. We propose alternative "big batch" SGD schemes that adaptively grow the batch size over time to maintain a nearly constant signal-to-noise ratio in the gradient approximation. The resulting methods have similar convergence rates to classical SGD, and do not require convexity of the objective. The high fidelity gradients enable automated learning rate selection and do not require stepsize decay. Big batch methods are thus easily automated and can run with little or no oversight.