Understanding the (un)interpretability of natural image distributions using generative models

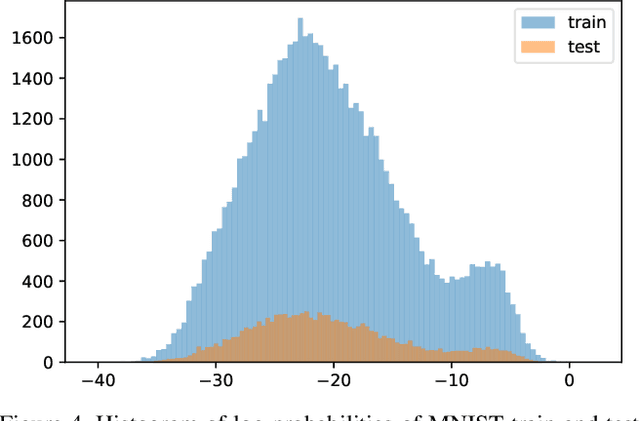
Probability density estimation is a classical and well studied problem, but standard density estimation methods have historically lacked the power to model complex and high-dimensional image distributions. More recent generative models leverage the power of neural networks to implicitly learn and represent probability models over complex images. We describe methods to extract explicit probability density estimates from GANs, and explore the properties of these image density functions. We perform sanity check experiments to provide evidence that these probabilities are reasonable. However, we also show that density functions of natural images are difficult to interpret and thus limited in use. We study reasons for this lack of interpretability, and show that we can get interpretability back by doing density estimation on latent representations of images.

Stacked U-Nets: A No-Frills Approach to Natural Image Segmentation

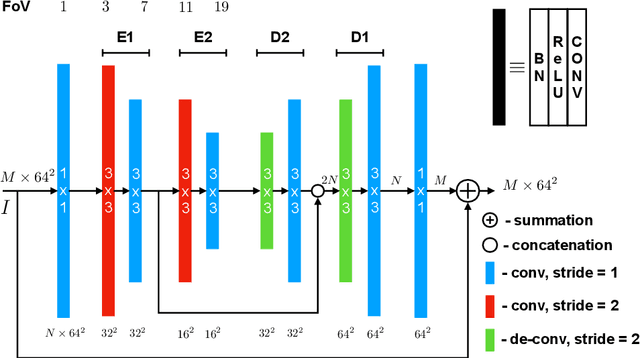
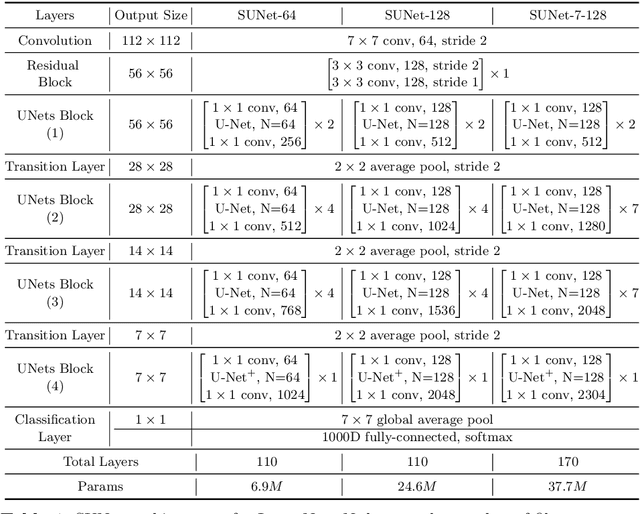
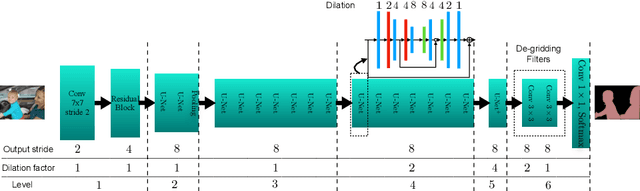
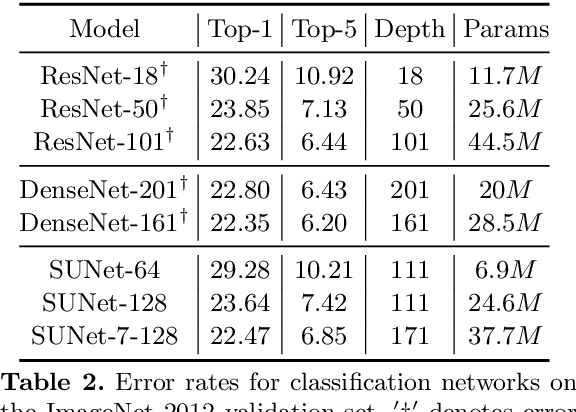
Many imaging tasks require global information about all pixels in an image. Conventional bottom-up classification networks globalize information by decreasing resolution; features are pooled and downsampled into a single output. But for semantic segmentation and object detection tasks, a network must provide higher-resolution pixel-level outputs. To globalize information while preserving resolution, many researchers propose the inclusion of sophisticated auxiliary blocks, but these come at the cost of a considerable increase in network size and computational cost. This paper proposes stacked u-nets (SUNets), which iteratively combine features from different resolution scales while maintaining resolution. SUNets leverage the information globalization power of u-nets in a deeper network architectures that is capable of handling the complexity of natural images. SUNets perform extremely well on semantic segmentation tasks using a small number of parameters.

Stabilizing Adversarial Nets With Prediction Methods

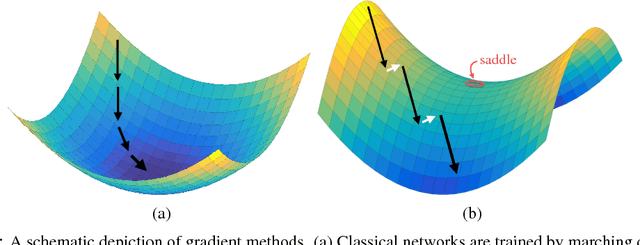
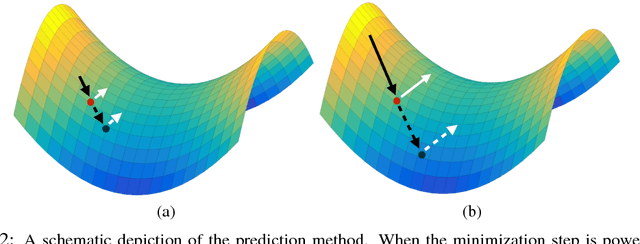
Adversarial neural networks solve many important problems in data science, but are notoriously difficult to train. These difficulties come from the fact that optimal weights for adversarial nets correspond to saddle points, and not minimizers, of the loss function. The alternating stochastic gradient methods typically used for such problems do not reliably converge to saddle points, and when convergence does happen it is often highly sensitive to learning rates. We propose a simple modification of stochastic gradient descent that stabilizes adversarial networks. We show, both in theory and practice, that the proposed method reliably converges to saddle points, and is stable with a wider range of training parameters than a non-prediction method. This makes adversarial networks less likely to "collapse," and enables faster training with larger learning rates.

Biconvex Relaxation for Semidefinite Programming in Computer Vision

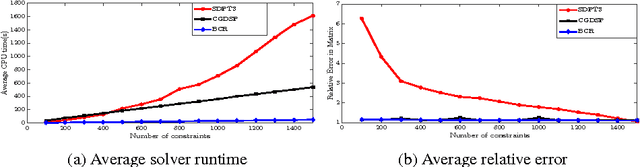
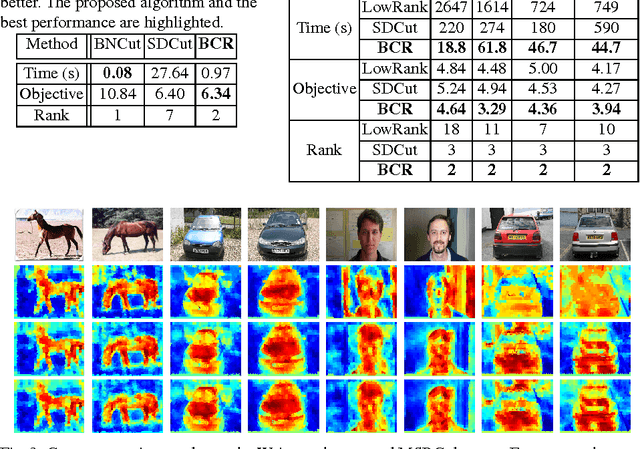
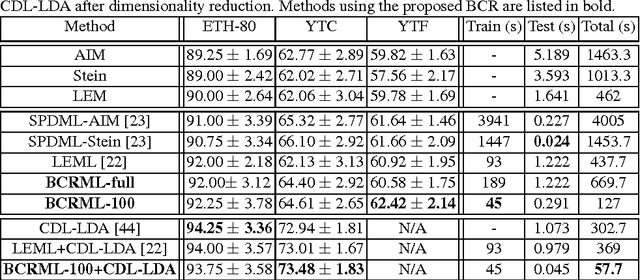
Semidefinite programming is an indispensable tool in computer vision, but general-purpose solvers for semidefinite programs are often too slow and memory intensive for large-scale problems. We propose a general framework to approximately solve large-scale semidefinite problems (SDPs) at low complexity. Our approach, referred to as biconvex relaxation (BCR), transforms a general SDP into a specific biconvex optimization problem, which can then be solved in the original, low-dimensional variable space at low complexity. The resulting biconvex problem is solved using an efficient alternating minimization (AM) procedure. Since AM has the potential to get stuck in local minima, we propose a general initialization scheme that enables BCR to start close to a global optimum - this is key for our algorithm to quickly converge to optimal or near-optimal solutions. We showcase the efficacy of our approach on three applications in computer vision, namely segmentation, co-segmentation, and manifold metric learning. BCR achieves solution quality comparable to state-of-the-art SDP methods with speedups between 4X and 35X. At the same time, BCR handles a more general set of SDPs than previous approaches, which are more specialized.

Weakly Supervised Learning of Heterogeneous Concepts in Videos

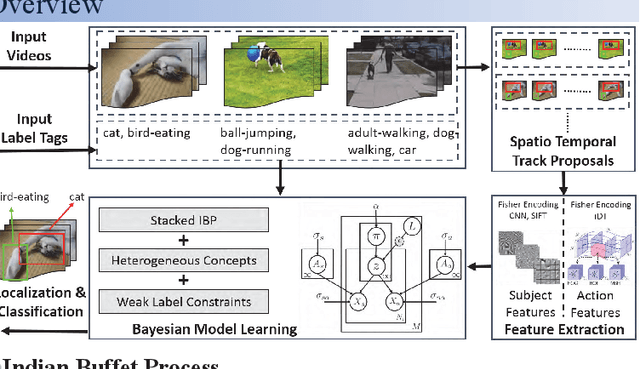
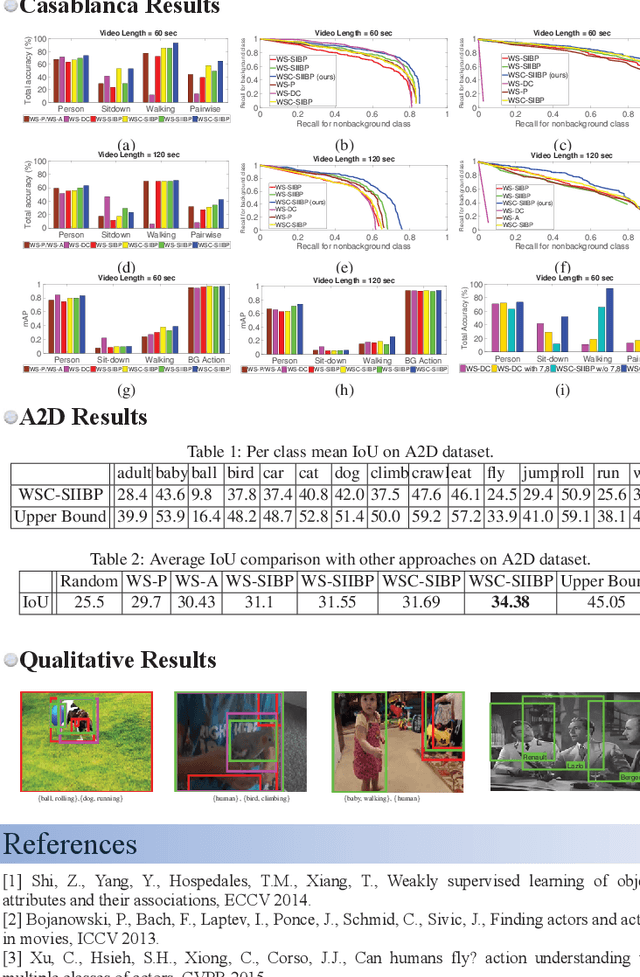
Typical textual descriptions that accompany online videos are 'weak': i.e., they mention the main concepts in the video but not their corresponding spatio-temporal locations. The concepts in the description are typically heterogeneous (e.g., objects, persons, actions). Certain location constraints on these concepts can also be inferred from the description. The goal of this paper is to present a generalization of the Indian Buffet Process (IBP) that can (a) systematically incorporate heterogeneous concepts in an integrated framework, and (b) enforce location constraints, for efficient classification and localization of the concepts in the videos. Finally, we develop posterior inference for the proposed formulation using mean-field variational approximation. Comparative evaluations on the Casablanca and the A2D datasets show that the proposed approach significantly outperforms other state-of-the-art techniques: 24% relative improvement for pairwise concept classification in the Casablanca dataset and 9% relative improvement for localization in the A2D dataset as compared to the most competitive baseline.

Estimating Sparse Signals with Smooth Support via Convex Programming and Block Sparsity

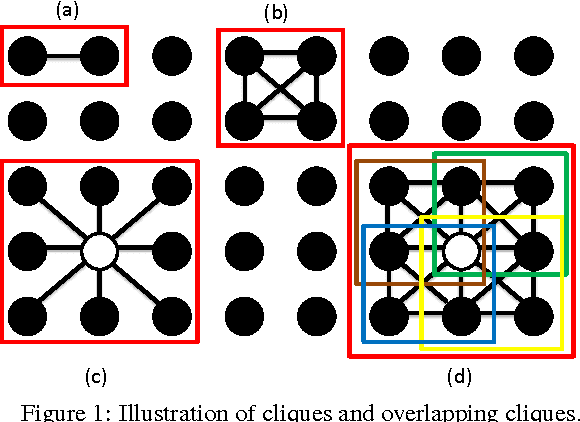
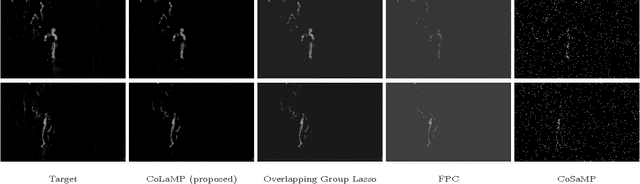
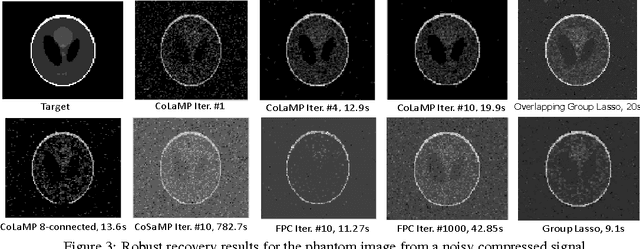
Conventional algorithms for sparse signal recovery and sparse representation rely on $l_1$-norm regularized variational methods. However, when applied to the reconstruction of $\textit{sparse images}$, i.e., images where only a few pixels are non-zero, simple $l_1$-norm-based methods ignore potential correlations in the support between adjacent pixels. In a number of applications, one is interested in images that are not only sparse, but also have a support with smooth (or contiguous) boundaries. Existing algorithms that take into account such a support structure mostly rely on non-convex methods and---as a consequence---do not scale well to high-dimensional problems and/or do not converge to global optima. In this paper, we explore the use of new block $l_1$-norm regularizers, which enforce image sparsity while simultaneously promoting smooth support structure. By exploiting the convexity of our regularizers, we develop new computationally-efficient recovery algorithms that guarantee global optimality. We demonstrate the efficacy of our regularizers on a variety of imaging tasks including compressive image recovery, image restoration, and robust PCA.