Estimating Sparse Signals with Smooth Support via Convex Programming and Block Sparsity
Paper and Code
May 06, 2016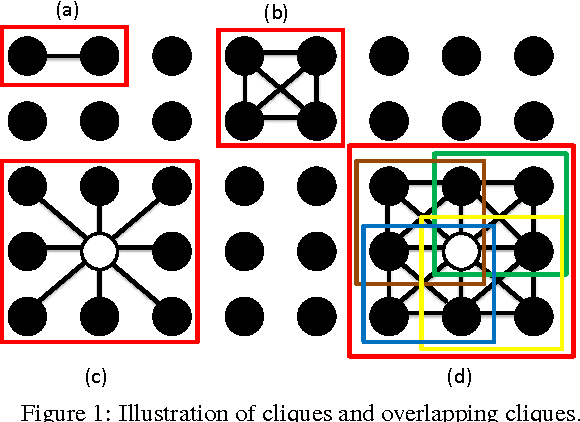
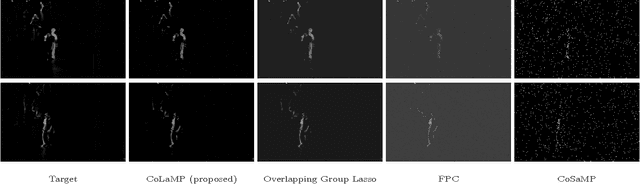
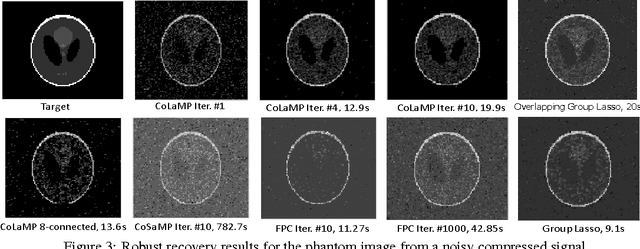

Conventional algorithms for sparse signal recovery and sparse representation rely on $l_1$-norm regularized variational methods. However, when applied to the reconstruction of $\textit{sparse images}$, i.e., images where only a few pixels are non-zero, simple $l_1$-norm-based methods ignore potential correlations in the support between adjacent pixels. In a number of applications, one is interested in images that are not only sparse, but also have a support with smooth (or contiguous) boundaries. Existing algorithms that take into account such a support structure mostly rely on non-convex methods and---as a consequence---do not scale well to high-dimensional problems and/or do not converge to global optima. In this paper, we explore the use of new block $l_1$-norm regularizers, which enforce image sparsity while simultaneously promoting smooth support structure. By exploiting the convexity of our regularizers, we develop new computationally-efficient recovery algorithms that guarantee global optimality. We demonstrate the efficacy of our regularizers on a variety of imaging tasks including compressive image recovery, image restoration, and robust PCA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge